Preguntas de test de electrostática en medios materiales (GIE)

De Laplace

1 Asociación de tres condensadores

Dado el sistema de tres condensadores de la figura,

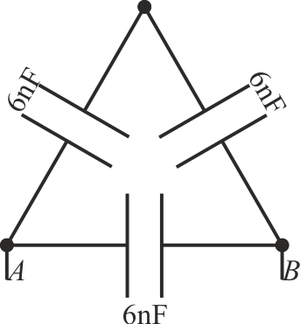
¿cuánto vale la capacidad equivalente entre A y B?

A 2 nF.
B 9 nF.
C 4 nF.
D 18 nF.

Solución

La respuesta correcta es la B.

El esquema del sistema es una asociación en paralelo entre el condensador de abajo y la asociación en serie de arriba.

La asociación en serie tiene la capacidad

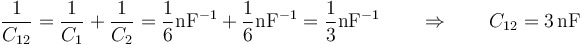
$\frac{1}{C_{12}}=\frac{1}{C_1}+\frac{1}{C_2}=\frac{1}{6}\mathrm{nF}^{-1}+\frac{1}{6}\mathrm{nF}^{-1}=\frac{1}{3}\mathrm{nF}^{-1}\qquad\Rightarrow\qquad C_{12}=3\,\mathrm{nF}$

y el conjunto completo

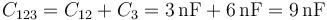
$C_{123}=C_{12}+C_3=3\,\mathrm{nF}+6\,\mathrm{nF}=9\,\mathrm{nF}$

2 Reparto de carga entre dos esferas

Dos esferas metálicas de 30 cm y 10 cm de radio están muy alejadas. La primera tiene una carga de 10 nC y la segunda está descargada. Se conectan por un hilo metálico. ¿Cómo se reparte la carga entre la grande y la pequeña?

A 50% - 50%
B 90% - 10%
C 75% - 25%
D 100% - 0%

Solución

La respuesta correcta es la C.

La carga pasa de la esfera cargada a la descargada hasta el momento en que se igualan los potenciales y se alcanza el equilibrio electrostático.

Si las esferas están muy alejadas, no se influyen mutuamente y el potencial al que se encuentra cada una es de la misma forma que el de una esfera sola. Por tanto, la condición de igualdad de potencial se da cuando

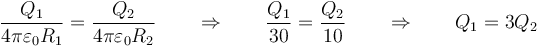
$\frac{Q_1}{4\pi\varepsilon_0R_1}=\frac{Q_2}{4\pi\varepsilon_0R_2}\qquad\Rightarrow\qquad \frac{Q_1}{30}=\frac{Q_2}{10}\qquad\Rightarrow\qquad Q_1=3Q_2$

Por tanto, en la esfera grande hay el triple de carga que en la pequeña (la misma proporción que entre los radios). Respecto del total

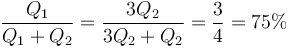
$\frac{Q_1}{Q_1+Q_2}=\frac{3Q_2}{3Q_2+Q_2}=\frac{3}{4}=75\%$

Es decir, el reparto es 75%-25%.

3 Sistema de tres conductores

Se tiene el sistema de conductores en equilibrio electrostático de la figura, en la que se han indicado algunas de las líneas de campo eléctrico

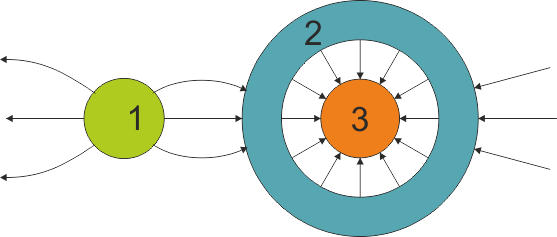
3.1 Pregunta 1

¿Qué podemos decir de los potenciales de cada conductor (tomando como origen de potencial el infinito)?

A $V 1 > V 2 > 0 > V 3$
B Tal situación es imposible.
C $V 1 > 0 > V 2 > V 3$
D $V 1 > V 2 > V 3 > 0$

Solución

La respuesta correcta es la C.

En electrostática, el campo siempre va de mayor a menor potencial. Estudiando la figura, vemos que eso implica que $V 1 > V 2 > V 3$ , pero en esto están de acuerdo todas las respuestas.

Se trata de ver el signo, si hay alguno de los potenciales son positivos o negativos, o si la situación es imposible porque se forma algún ciclo cerrado.

Puesto que hay líneas que van del conductor 1 al infinito, esto quiere decir que $V 1 > 0$ . Además hay líneas que van del infinito al conductor 2, por lo que $V 2 < 0$ . Esto no es contradictorio con que $V 1 > V 2$ . Por tanto, la respuesta correcta es

$V_1 > 0 > V_2 > V_3\,$

3.2 Pregunta 2

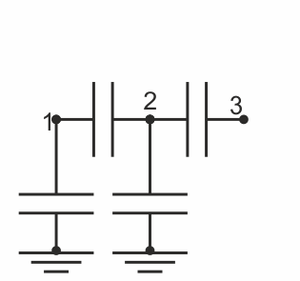
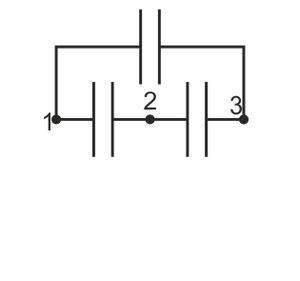
¿Cómo sería el sistema de condensadores que representa a este sistema de conductores?

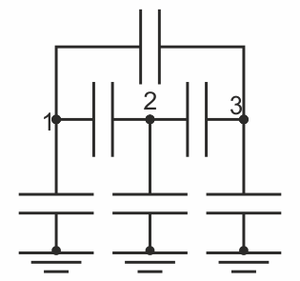
A	B


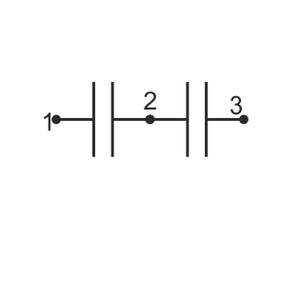
C	D

Solución

La respuesta correcta es la B.

Un sistema de conductores se puede modelar por un sistema de condensadores, donde cada uno representa la porción de líneas de campo que van de uno a otro. En principio, puede haber como máximo un condensador entre cada dos conductores, más uno de cada conductor a tierra (líneas que van o vuelven del infinito).

Ahora bien, en este sistema, es imposible que haya líneas de campo que vayan del conductor 3 al 1, o del conductor 3 al infinito, ya que lo impide el conductor 2. Por tanto, hay que eliminar esos dos condensadores y el sistema se reduce a la opción B.

4 Condensador con dieléctrico

Se tiene un condensador plano formado por dos placas circulares de radio 10 cm separadas una distancia de 1 mm. Entre ellas hay una lámina de dieléctrico de permitividad 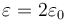$\varepsilon=2\varepsilon_0$ . La lámina llena todo el espacio entre las placas. Se aplica entre las placas una diferencia de potencial de 100 V

4.1 Pregunta 1

¿Cuánto vale la energía almacenada en el sistema?

A 2.78 μJ.
B 0.556 nJ.
C 1.39 μJ.
D 5.56 μJ.

Solución

La respuesta correcta es la A.

La energía almacenada en un condensador es

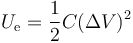
$U_\mathrm{e}=\frac{1}{2}C(\Delta V)^2$

siendo la capacidad

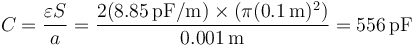
$C=\frac{\varepsilon S}{a}=\frac{2(8.85\,\mathrm{pF}/\mathrm{m})\times(\pi (0.1\,\mathrm{m})^2)}{0.001\,\mathrm{m}}=556\,\mathrm{pF}$

y la energía almacenada

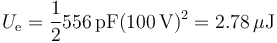
$U_\mathrm{e}=\frac{1}{2}556\,\mathrm{pF}(100\,\mathrm{V})^2=2.78\,\mu\mathrm{J}$

4.2 Pregunta 2

Sin desconectar la fuente se retira la lámina de dieléctrico. En este proceso la energía almacenada…

A aumenta al cuádruple.
B aumenta al doble.
C se reduce a la mitad.
D se queda igual.

Solución

La respuesta correcta es la C.

Al retirar el dieléctrico, la permitividad se reduce a la mitad de la anterior y, por tanto, la capacidad también se divide por 2

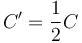
$C'=\frac{1}{2}C$

Puesto que la fuente permanece conectada, la d.d.p. entre las placas no cambia y

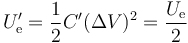
$U'_\mathrm{e}=\frac{1}{2}C'(\Delta V)^2=\frac{U_\mathrm{e}}{2}$

5 Condensador relleno de papel

Se construye un condensador plano colocando horizontalmente un disco de radio 10 cm, sobre él una hoja de papel de 0.1 mm de espesor con permitividad 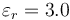$\varepsilon_r = 3.0$ y sobre ésta se apoya otro disco metálico del mismo radio.

5.1 Pregunta 1

¿Cuánto vale la capacidad del condensador resultante?

A 0.085 pF.
B 8.34 nF.
C 2.78 nF.
D 26.6 nF.

Solución

La respuesta correcta es la B.

Aplicamos la fórmula de la capacidad de un condensador plano

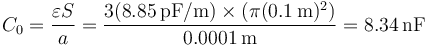
$C_0=\frac{\varepsilon S}{a}=\frac{3(8.85\,\mathrm{pF}/\mathrm{m})\times(\pi (0.1\,\mathrm{m})^2)}{0.0001\,\mathrm{m}}=8.34\,\mathrm{nF}$

5.2 Pregunta 2

La placa superior se eleva una distancia de 0.1 mm, separándola del papel, ¿cuánto vale la nueva capacidad del condensador?

A 4.17 nF.
B 11.12 nF
C 2.09 nF.
D 16.7 nF

Solución

La respuesta correcta es la C.

Cuando se levanta la placa el cálculo no consiste en sustituir a por 2a, ya que una hoja de papel es un sólido, que no se expande para ocupar el volumen restante.

Al levantar el disco lo que ocurre es que el papel se queda como estaba y además aparece una capa de aire entre el papel y el disco. El sistema ahora es uno de dos capas, que se puede modelar como dos condensadores en serie.

La capacidad de la capa de aire es 1/3 de la del papel (porque la permitividad relativa de éste es 3.0)

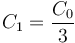
$C_1 = \frac{C_0}{3}$

y por tanto la capacidad del conjunto cumple

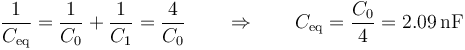
$\frac{1}{C_\mathrm{eq}}=\frac{1}{C_0}+\frac{1}{C_1}=\frac{4}{C_0}\qquad\Rightarrow\qquad C_\mathrm{eq}=\frac{C_0}{4}=2.09\,\mathrm{nF}$

6 Carga frente a esfera

Una esfera conductora se encuentra conectada a tierra. Frente a ella se coloca una carga puntual positiva. ¿Como son el potencial y la carga de la esfera?

A $V = 0$ y $Q < 0$
B $V = 0$ y $Q = 0$
C $V > 0$ y $Q = 0$
D $V > 0$ y $Q > 0$

Solución

La respuesta correcta es la A.

La esfera está a tierra, por lo que su potencial es 0, por definición.

Cuando se coloca frente a ella una carga positiva, ésta atrae a las cargas negativas del conductor y repele a las positivas. Al estar conectada a tierra, que es un depósito infinito de cargas, se produce una acumulación neta de cargas negativas en la esfera, por lo que

$V=0\qquad\qquad Q < 0$

7 Dieléctrico con dos capas

Se tiene el condensador de la figura, formado por dos placas conductoras paralelas de sección $S$ y distancia entre placas $a$ . Entre ellas la mitad del espacio está ocupado por un dieléctrico ideal de permitividad relativa 1.5 y la otra mitad por uno de permitividad 3.0, siendo la frontera paralela a las placas. La capacidad del condensador en vacío en ausencia de los dieléctricos es $C 0$ .

7.1 Pregunta 1

¿Cuánto vale la capacidad de este condensador?

A $C = 4.5 C 0$
B $C = 2.25 C 0$
C $C = 0.5 C 0$
D $C = 2.0 C 0$

Solución

La respuesta correcta es la D.

La capacidad en vacío es

$C_0=\frac{\varepsilon_0 S}{a}$

La de cada una de las capas de dieléctrico vale

$C_1=\frac{1.5\varepsilon_0 S}{a/2}=3C_0\qquad\qquad C_2=\frac{3.0\varepsilon_0 S}{a/2}=6C_0$

y la de la asociación en serie

$\frac{1}{C_\mathrm{eq}}=\frac{1}{3C_0}+\frac{1}{6C_0}=\frac{1}{2C_0}\qquad\Rightarrow\qquad C_\mathrm{eq}=2C_0$

7.2 Pregunta 2

Suponga que este condensador se conecta a una fuente de tensión $V 0$ . Si $E 1$ es el campo en el material de permitividad 1.5 y $E 2$ en el de permitividad 3.0, ¿cómo se relacionan estos dos campos?

A Puede darse cualquiera de las otras tres posibilidades.
B $E 1 > E 2$
C $E 1 < E 2$
D $E 1 = E 2$

Solución

La respuesta correcta es la B.

El campo en cada una de las capas es uniforme e igual en módulo a

$E_i=\frac{\Delta V_i}{a/2}$

La diferencia de potencial en cada capa la obtenemos con el circuito equivalente. Al tratarse de dos condensadores en serie, la carga en ellos es la misma. Por tanto

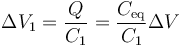
$\Delta V_1 = \frac{Q}{C_1}=\frac{C_\mathrm{eq}}{C_1}\Delta V$

Esto nos da, en cada caso,

$\Delta V_1=\frac{2C_0}{3C_0}\Delta V = \frac{2}{3}\Delta V\qquad\qquad \Delta V_2=\frac{2C_0}{6C_0}\Delta V = \frac{1}{3}\Delta V$

La comparación entre los campos es entonces igual a

$\frac{E_1}{E_2}=\frac{\Delta V_1}{\Delta V_2}=2$

Por tanto el campo 1 es más intenso que el 2. Más en general se tiene que

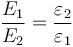
$\frac{E_1}{E_2}=\frac{\varepsilon_2}{\varepsilon_1}$

y el campo es más intenso donde la permitividad sea más pequeña.

8 Dos conductores enfrentados

Se colocan dos conductores uno frente al otro. El primero tiene $Q 1 > 0$ y el segundo $Q 2 = 0$ . No hay más cargas ni conductores en el sistema. ¿Qué podemos decir de sus potenciales?

A $V 1 > 0$ , $V 2 < 0$ .
B $V 1 > 0$ , $V 2 > 0$ .
C $V 1 = 0$ , $V 2 < 0$ .
D $V 1 > 0$ , $V 2 = 0$ .

Solución

La respuesta correcta es la B.

Si el conductor 1 tiene carga positiva quiere decir que las líneas de campo saldrán de él, por ley de Gauss (el flujo debe ser positivo). Algunas de estas líneas de campo irán a parar al conductor 2.

Puesto que el conductor 2 tiene carga nula, el flujo alrededor de él debe anularse. Por tanto, deben salir de él tantas líneas como entran. Las líneas que salen no pueden volver al 1, sino ir al infinito, que está apotencial 0. Por tanto

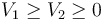
$V_1 \geq V_2 \geq 0$

9 Dos superficies esféricas

Se tienen dos superficies conductoras esféricas concéntricas, de radios 1 cm y 3 cm, respectivamente. Inicialmente la interior (1) almacena una carga de $-$ 40 nC y la exterior (2) una de +20 nC.

9.1 Pregunta 1

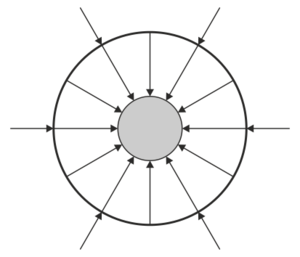
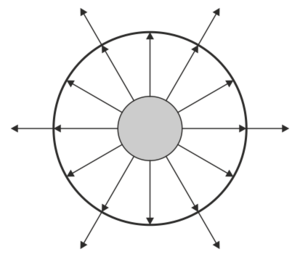
¿Cuál de las siguientes figuras describe adecuadamente el campo eléctrico en el sistema?

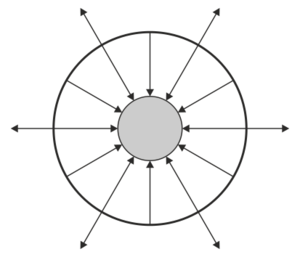
A	B


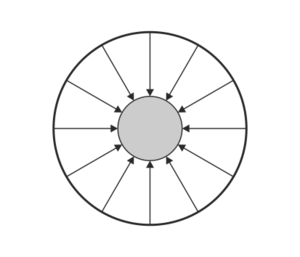
C	D

Solución

La respuesta correcta es la B.

Si aplicamos la ley de Gauss a una superficie que envuelva todo el sistema tenemos que

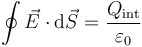
$\oint\vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}$

siendo la carga encerrada la suma de la de las dos esferas

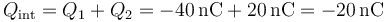
$Q_\mathrm{int}=Q_1+Q_2=-40\,\mathrm{nC}+20\,\mathrm{nC}=-20\,\mathrm{nC}$

por tanto, el flujo es negativo, lo cual quiere decir que en el campo exterior a las dos esferas va hacia adentro.

9.2 Pregunta 2

Se conectan las dos esferas por un cable. Una vez que se alcanza el equilibrio electrostático, ¿cómo queda el reparto de cargas entre las dos?

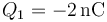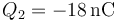
A $Q_1=-2\,\mathrm{nC}$ , $Q_2 = -18\,\mathrm{nC}$
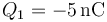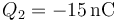
B $Q_1=-5\,\mathrm{nC}$ , $Q_2 = -15\,\mathrm{nC}$
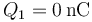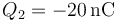
C $Q_1=0\,\mathrm{nC}$ , $Q_2 = -20\,\mathrm{nC}$
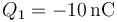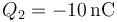
D $Q_1=-10\,\mathrm{nC}$ , $Q_2 = -10\,\mathrm{nC}$

Solución

La respuesta correcta es la C.

Cuando se conectan las dos esferas, pasa carga de una a la otra. Los dos conductores pasan a formar un solo conductor, con un hueco y una superficie exterior. Puesto que no hay nada en el interior del hueco, la carga en la pared del hueco (que es la esfera 1) es nula y toda la carga está en la superficie exterior (que es la esfera 2).

Dicho de otra forma, por la repulsión entre las cargas, éstas se alejan todo lo que pueden y por ello se van a la superficie exterior.

También puede demostrarse suponiendo que hay cargas en cada una de las esferas. En ese caso, los potenciales respectivos valen

$V_1=\frac{Q_1}{4\pi\varepsilon_0a}+\frac{Q_2}{4\pi\varepsilon_0 b}\qquad\qquad V_2=\frac{Q_1}{4\pi\varepsilon_0b}+\frac{Q_2}{4\pi\varepsilon_0 b}$

y para que estas dos cantidades sean iguales debe ser $Q 1 = 0$ .

10 Tres placas circulares

Tres placas conductoras circulares de radio 12 cm se encuentran situadas paralelamente con una distancia de 1 mm entre ellas. El espacio intermedio está vacío. La placa central se encuentra a un potencial de 100 V, mientras que las exteriores están puestas a tierra.

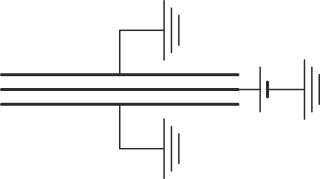
La energía electrostática almacenada en el sistema vale…

A 4 μJ
B 8 μJ
C 2 μJ
D 1 μJ

Solución

La respuesta correcta es la A.

Aunque pueda parecer lo contrario, estos dos condensadores están en paralelo, ya que al estar las dos placas exteriores a tierra, es como si además estuvieran conectadas entre sí. Por tanto, la capacidad equivalente es

$C_\mathrm{eq}=2C_0=2\frac{\varepsilon_0\pi R^2}{a}=0.4\,\mathrm{nF}$

por lo que la energía almacenada vale

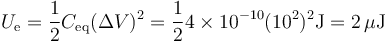
$U_\mathrm{e}=\frac{1}{2}C_\mathrm{eq}(\Delta V)^2=\frac{1}{2}4\times 10^{-10}(10^2)^2\mathrm{J}= 2\,\mu\mathrm{J}$

11 Comparación de dos condensadores

Se tienen dos condensadores planos de las mismas dimensiones (sección y espesor). El 1 está relleno de un dieléctrico con permitividad relativa 3.0 y el 2 de un dieléctrico con permitividad 1.5. En un momento dado, los dos están cargados con la misma carga $Q 0$ . ¿En cuál de ellos es mayor el campo eléctrico interior?

A En el 2.
B Vale lo mismo en los dos.
C En el 1.
D No hay suficiente información para saberlo.

Solución

La respuesta correcta es la A.

El campo eléctrico en cada uno es igual a

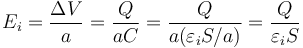
$E_i=\frac{\Delta V}{a}=\frac{Q}{aC}=\frac{Q}{a(\varepsilon_i S/a)}=\frac{Q}{\varepsilon_i S}$

Entonces, a igualdad de carga, el campo eléctrico es más pequeño cuanto mayor sea la permitividad. Por tanto, el campo eléctrico es mayor en el condensador 2.

Preguntas de test de electrostática en medios materiales (GIE)

De Laplace

Contenido

1 Asociación de tres condensadores

2 Reparto de carga entre dos esferas

3 Sistema de tres conductores

3.1 Pregunta 1

3.2 Pregunta 2

4 Condensador con dieléctrico

4.1 Pregunta 1

4.2 Pregunta 2

5 Condensador relleno de papel

5.1 Pregunta 1

5.2 Pregunta 2

6 Carga frente a esfera

7 Dieléctrico con dos capas

7.1 Pregunta 1

7.2 Pregunta 2

8 Dos conductores enfrentados

9 Dos superficies esféricas

9.1 Pregunta 1

9.2 Pregunta 2

10 Tres placas circulares

11 Comparación de dos condensadores

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES