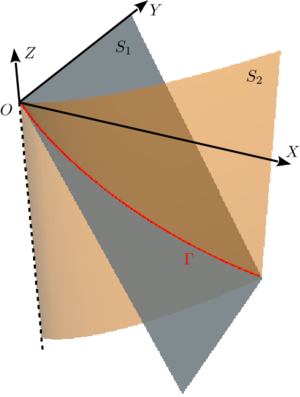
Partícula con trayectoria dada
De Laplace
Contenido |
1 Enunciado
Un cuerpo material puntual P, se mueve respecto de un sistema de referencia cartesiano fijo OXYZ. A partir del instante inicial t = 0, dicho movimiento está descrito por las ecuaciones horarias
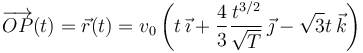
donde t es el tiempo, y v0 y T, parámetros de valor conocido.
- Obtenga las ecuaciones de la trayectoria.
- Calcule los vectores velocidad y aceleración instantánea,
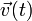 y
y 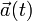 .
.
- Obtenga las expresiones intrínsecas de dichos vectores. Determine la ley horaria s(t) para la distancia recorrida por la partícula sobre su trayectoria, desde la posición que ocupaba en el instante inicial: es decir s(t = 0) = 0.
- Calcule los valores de las magnitudes cinemáticas indicadas en el apartado anterior en el instante inicial t = 0. Discuta los resultados obtenidos.
2 Solución
2.1 Ecuaciones de la trayectoria
Vamos a expresar la curva como intersección de dos superficies. La expresión paramétrica de la curva puede escribirse como
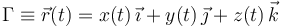
Donde
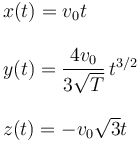
Podemos despejar t en función de x en la primera expresión. Sustituyendo en las dos siguientes obtenemos dos superficies
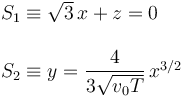
La primera es un plano, mientras que la segunda es la superficie creada al prolongar una curva definida en el plano OXY paralelamente al eje OZ. La figura muestra como la intersección de estas dos superficies define la curva Γ. Para hacer la figura se ha tomado v0 = 1 y T = 1.
2.2 Velocidad y aceleración
Derivamos respecto al tiempo para obtener el vector velocidad
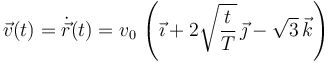
Derivamos otra vez para calcular el vector aceleración
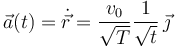
2.3 Expresiones intrínsecas
El módulo del vector velocidad es
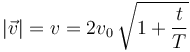
Calculamos el vector tangente a la trayectoria
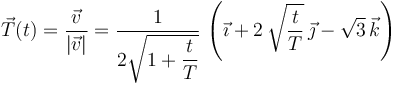
La aceleración tangencial es
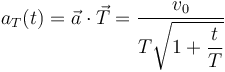
El vector aceleración tangencial es
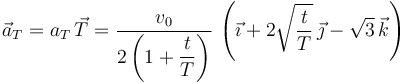
Podemos calcular el vector aceleración normal
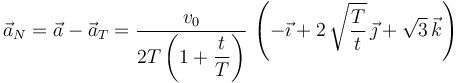
La aceleración es el módulo de este vector
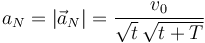
Y el vector normal
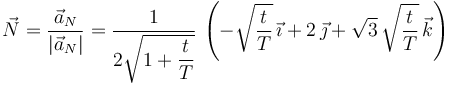
El vector binormal es
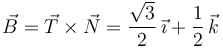
Este vector es constante y perpendicular al plano S1. Esto se debe a que la trayectoria es una curva plana.
2.3.1 Parámetro arco
Para calcular el parámetro arco sumamos los desplazamientos infinitesimales sobre la trayectoria
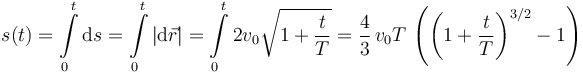
2.3.2 Curvatura y radio de curvatura
La curvatura es
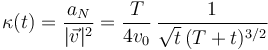
y el radio de curvatura
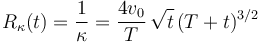
2.4 Valores en t = 0
Veamos los valores de las magnitudes cinemáticas en t = 0
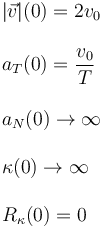
Vemos que la aceleración normal, y por tanto la curvatura, se hacen infinitas en t = 0. Por tanto el radio de curvatura se anula en el instante inicial. La curva es singular en ese instante inicial. Desde el punto de vista físico, esto indica que no describimos bien lo que pasa cerca del instante inicial. La escala espacial típica del movimiento es demasiado pequeña. Si esto fuese el resultado de un experimento, habría que mirar con más detalle que es lo que pasa en ese instante inicial. Para t > 0 la expresión paramétrica dada si es la adecuada para describir el movimiento de la partícula.