Movimiento sobre curvas y superficies (GIOI)
De Laplace
Contenido |
1 Movimiento sobre una superficie
Un caso de partícula vinculada es aquél en que se ve a obligada a moverse sobre una superficie. Esta superficie puede ser material o simplemente geométrica. Por ejemplo, una partícula que se mueve sobre el interior de un cuenco hemisférico, o una lenteja que oscila en el extremo de un hilo flexible, están sometidos al mismo vínculo de moverse sobre una superficie esférica.
El vínculo de moverse sobre una superficie puede ser unilateral o bilateral. En el caso péndulo con hilo flexible, la ligadura es unilateral, ya que la distancia al centro es menor o igual a L, la longitud del hilo. Si en vez de un hilo tenemos una barra rígida, el vínculo es bilateral, ya que la distancia al centro es siempre igual a L.
Cunado una partícula se mueve sobre una superficie fijada experimenta una fuerza de reacción vincular, que se compone dos partes:
- Una fuerza perpendicular a la superficie, que es la responsable de que la partícula se mueva sobre ella. Por la tercera ley de Newton, esta fuerza será igual y opuesta a la componente normal que la partícula ejerce sobre la superficie.
- Una fuerza de rozamiento, tangente a la superficie. En los casos de contacto seco, sigue las leyes de Coulomb del rozamiento.
En el caso de un vínculo liso (sin rozamiento), la fuerza de reacción es puramente perpendicular a la superficie.
1.1 Plano inclinado
Un ejemplo sencillo lo tenemos en el plano inclinado. Consideremos un bloque de masa m situada sobre un plano inclinado un ángulo β. El coeficiente de rozamiento estático es μ y el dinámico es μd (μd < μ). ¿Cuánto vale el ángulo mínimo para que deslice? Si lo hace, ¿cuánto vale su aceleración?
Las fuerzas que actúan sobre la masa son su peso, la reacción normal del plano y la fuerza de rozamiento. Para que no haya deslizamiento, la suma de las tres debe ser nula. Si usamos un sistema de ejes en el que ele eje OX es tangente al plano y el OY es perpendicular a él, el peso puede escribirse como
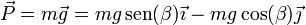
mientras que la reacción normal y la fuerza de rozamiento son de la forma

Sumando las tres
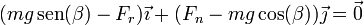
Puesto que las dos componentes deben anularse

Dividiendo una por la otra
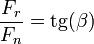
pero, por las leyes del rozamiento

lo que nos da la condición para el ángulo
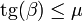
Existe un ángulo crítico βc = arctg(μ) por debajo del cual el bloque se queda un equilibrio y por encima del cual desliza.
Cuando lo hace, el bloque adquiere una aceleración paralela al plano, con lo que la segunda ley de Newton nos da ahora
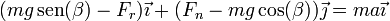
Separando en componentes

En el caso del rozamiento dinámico seco

lo que nos da la aceleración, independiente de la masa,
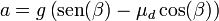
Obsérvese que, puesto que μd < μ existe un rango de ángulos tales que si el bloque está en reposo, permanece en reposo, pero si está en movimiento, continúa haciéndolo aceleradamente. Esto quiere decir en la práctica lo siguiente. Si vamos aumentando la inclinación del plano hasta un poco por debajo la posición de deslizamiento inminente, y ahora le pegamos un golpecito al plano, rompiendo los enlaces causantes del rozamiento estático, el bloque empieza a moverse, ya que la fuerza de rozmainto dinámica no es capaz de contenerlo.
1.2 Partícula en un cuenco
El movimiento sobre una superficie no tiene por qué ser un movimiento plano, y el vector perpendicular a la superficie no tiene por qué coincidir con  , el vector normal a la trayectoria. Por ejemplo, consideremos de nuevo la particula que se mueve en el interior de un cuenco esférico sin rozamiento, sometida a la acción de su peso. La segunda ley de Newton se escribe
, el vector normal a la trayectoria. Por ejemplo, consideremos de nuevo la particula que se mueve en el interior de un cuenco esférico sin rozamiento, sometida a la acción de su peso. La segunda ley de Newton se escribe
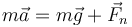
donde 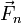 va en la dirección radial hacia adentro
va en la dirección radial hacia adentro
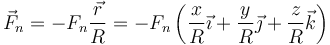
lo que nos da las tres ecuaciones escalares
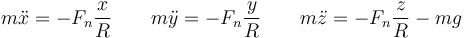
junto con la ecuación del vínculo
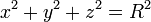
En las ecuaciones anteriores Fn no es una constante. Es el módulo de la fuerza de reacción que ejerce el cuenco. Esta fuerza es una función de la posición y del tiempo.
Así, en la figura vemos la solución (obtenida numéricamente) de una partícula en el interior de una esfera a la cual se le ha comunicado una cierta velocidad lateral inicial. Vemos que el peso (flecha verde) es una fuerza constante mientras que la reacción de la superficie (flecha azul) es siempre radial hacia adentro, pero su módulo puede variar considerablemente. La suma de estas dos fuerzas produce una aceleración con una dirección variable, con una componente normal que en ningún caso va en la dirección de la normal a la superficie.
Un caso particular soluble de la partícula en la esfera sin rozamiento consiste en que si se le comunica una velocidad horizontal adecuada, se puede conseguir que describa circunferencias horizontales
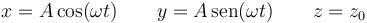
Sustituyendo en las ecuaciones de movimiento queda

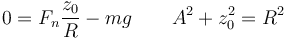
De estas ecuaciones obtenemos que
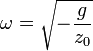
lo que nos dice que este movimiento sólo es posible si z0 < 0, esto es, en el hemisferio inferior. La rapidez que hay que comunicarle a la partícula debe ser, por tratarse de un movimiento circular
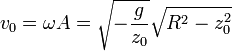
y la fuerza de reacción del cuenco tiene por módulo

La dirección de esta fuerza, según hemos dicho, es hacia el centro de la esfera, mientras que el vector normal a la trayectoria apunta en la dirección normal (la única que hay en este caso), y es horizontal.
2 Movimiento a lo largo de una curva
Cuando una partícula se ve obligada a seguir una curva determinada, por ejemplo, un automóvil siguiendo una carretera, o una anilla ensartada en un alambre, experimenta una fuerza de reacción vincular que, como en el caso de la superficie, se compone de:
- una componente perpendicular a la curva, no necesariamente en el sentido de
 , el unitario en la dirección del vector normal.
, el unitario en la dirección del vector normal.
- una fuerza de rozamiento en la dirección tangente a la curva.
En el caso de un vínculo liso, sin rozamiento, la fuerza de reacción es puramente perpendicular a la trayectoria.
En el movimiento a lo largo de la curva, el vector tangente a la trayectoria está definido por la propia curva, por lo que la partícula solo puede cambiar su dirección en la foirma que el alambre se lo permita. El problema dinámico se reduce entonces a determinar cómo se mueve la partícula a lo largo de la curva. Esto se consigue estudiando la aceleración tangencial y la variación de la distancia recorrida sobre la curva

En el caso de que no haya rozamiento, las fuerzas de reacción no tienen componente tangencial y en el segundo miembro solo aparecen las fuerzas aplicada, como el peso.
Un ejemplo sencillo lo tenemos en un coche que describe una curva circular
- En ausencia de rozamiento y de peralte, la fuerza de reacción del suelo es puramente vertical, como lo es el peso, el coche no puede tomar la curva, ya que no hay fuerza horizontal. Necesariamente derrapa.
- Una curva peraltada, posee una inclinación hacia el interior de la curva, lo que proporciona una componente radial a la fuerza de reacción, permitiendo el giro incluso en ausencia de rozamiento. Eso sí, solo a una velocidad concreta.
- El rozamiento lateral debido a los neumáticos es una fuerza radial, responsable, en las curvas llanas no peraltadas, de la fuerza normal hacia el interior de la curva, que permite el giro sin derrapar.
- La combinación de rozamiento y peralte permite un amplio rango de velocidades con las que tomar la curva sin derrapar.
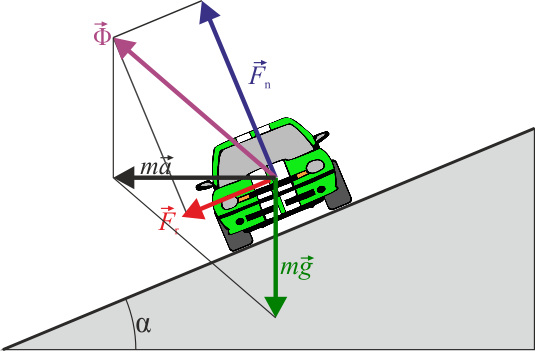
Un ejemplo más elaborado sería el de una cuenta de collar que desliza sin rozamiento por un alambre helicoidal con eje vertical, siendo β la inclinación de la hélice. La componente tangencial del peso es
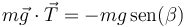
(como un plano inclinado, solo que este está “enrollado”). Por tanto, la ecuación de movimiento es
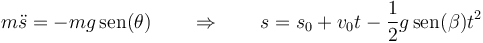
es decir, la partícula sigue un movimiento uniformemente acelerado a lo largo de la hélice.