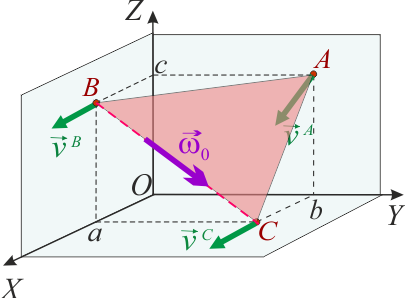
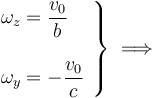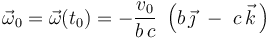Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales, F1 GIA (Ene, 2018)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Velocidades de los vértices del triángulo en un instante
- 2.2 Vector rotación instantánea

1 Enunciado

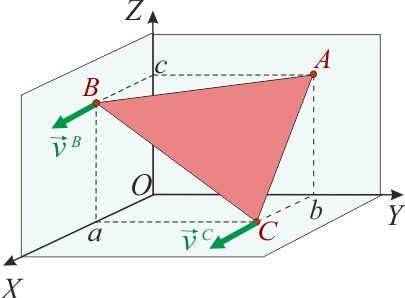
Un sólido rígido con forma de triángulo plano se mueve con sus vértices

A

,

B

y

C

en contacto permanente con los respectivos planos

O Y Z

,

O X Z

y

O X Y

, de manera que en todo momento se verificará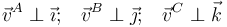 $\vec{v}^A\perp\vec{\imath}\mathrm{;}\quad \vec{v}^B\perp\vec{\jmath}\mathrm{;}\quad \vec{v}^C\perp\vec{k}$

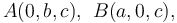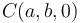En un determinado instante en que los vértices del triángulo ocupan los puntos de coordenadas conocidas $A(0,b,c)\mathrm{,}\;\; B(a,0,c)\mathrm{,}\,$ y $\, C(a,b,0)$ , se comprueba que las velocidades de $B$ y $C$ son idénticas ( 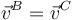$\vec{v}^B=\vec{v}^C$ ), siendo $v 0$ el módulo de ambas.

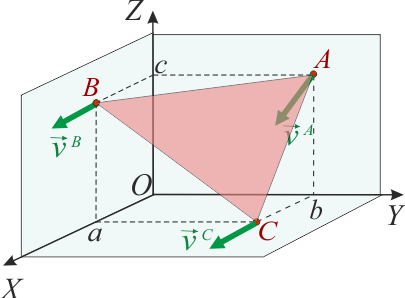
Determine las componentes de la velocidad del vértice $A$ en dicho instante.
También en el instante considerado, ¿qué dirección debe tener el vector rotación $\vec{\omega}$ , característico del movimiento del sólido? Justifique su respuesta y obtenga la expresión analítica (componentes) de dicho vector.

2 Solución

La condición geométrica de rigidez, característica del modelo de sólido rígido para los cuerpos materiales, se traduce en la condición cinemática de rigidez para el campo de velocidades que a cada punto del sólido le hace corresponder un vector que describe la velocidad instantánea de dicho punto, cuando el sólido se encuentra en movimiento respecto de un determinado sistema de referencia fijo, $O X Y Z$ :

$\tau_{{}_\mathrm{SR}}=\{P_1,P_2,...,P_i,...\}\mathrm{,}\quad\mathrm{tales}\;\;\mathrm{que}\;\;\, \overrightarrow{OP}_i=\vec{r}_i(t)\mathrm{,}\;\;\forall\,i\; \;\Longrightarrow \;\; \frac{\mathrm{d}\vec{r}_i(t)}{\mathrm{d}t}=\vec{v}^{P_i}(t)\mathrm{,}\;\;\forall\,i\; \;\longrightarrow \;\;\left\{\vec{v}^{P_1}(t),\vec{v}^{P_2}(t),...,\vec{v}^{P_i}(t),...\right\}$

Esta condición establece que dicho campo de velocidades es equiproyectivo: las velocidades instantáneas de cualquier par de puntos de un solido rígido 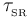$\tau_{{}_\mathrm{SR}}$ en movimiento tienen proyecciones idénticas sobre la recta que pasa por dichos puntos. Esto puede expresarse matemáticamente de la siguiente forma:

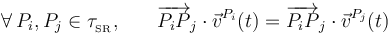
$\forall\, P_i\mathrm{,}\!\ P_j\in \tau_{{}_\mathrm{SR}}\mathrm{,}\qquad \overrightarrow{P_iP}_j \cdot \vec{v}^{P_i}(t)=\overrightarrow{P_iP}_j \cdot \vec{v}^{P_j}(t)$

en cada instante de tiempo.

2.1 Velocidades de los vértices del triángulo en un instante

En el sistema bajo estudio, los vértices $A$ , $B$ y $C$ de un sólido rígido triangular se mueven deslizando por tres planos ortogonales que tomaremos como los respectivos planos cartesianos. Por tanto, se tendrá que, en general:

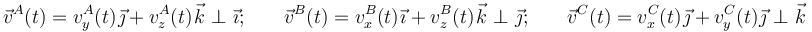
$\vec{v}^A(t)=v_y^A(t)\!\ \vec{\jmath}\ +\ v_z^A(t)\!\ \vec{k}\!\ \perp\!\ \vec{\imath}\mathrm{;}\qquad\vec{v}^B(t)=v_x^B(t)\!\ \vec{\imath}\ +\ v_z^B(t)\!\ \vec{k}\!\ \perp\!\ \vec{\jmath}\mathrm{;}\qquad\vec{v}^C(t)=v_x^C(t)\!\ \vec{\jmath}\ +\ v_y^C(t)\!\ \vec{\jmath}\!\ \perp\!\ \vec{k}$

En este apartado del ejercicio se pide determinar la velocidad instantánea del punto

A

en un instante

t 0

en que las de los otros dos vértices se igualan, siendo

v 0

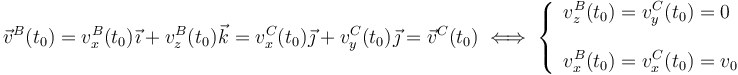
el valor de sus módulos: $\vec{v}^B(t_0)=v_x^B(t_0)\!\ \vec{\imath}\ +\ v_z^B(t_0)\!\ \vec{k}=v_x^C(t_0)\!\ \vec{\jmath}\ +\ v_y^C(t_0)\!\ \vec{\jmath}=\vec{v}^C(t_0)\; \Longleftrightarrow \; \left\{\begin{array}{l} \displaystyle v_z^B(t_0)=v_y^C(t_0)=0\\ \\ \displaystyle v_x^B(t_0)=v_x^C(t_0)=v_0 \end{array}\right.$

Por tanto, en el instante considerado, se tendrá...

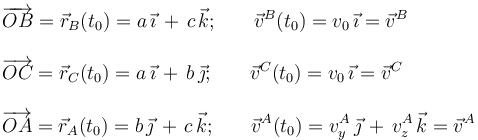
$\begin{array}{l} \displaystyle \overrightarrow{OB}=\vec{r}_B(t_0)=a\!\ \vec{\imath}\!\ +\!\ c\!\ \vec{k}\mathrm{;}\qquad\vec{v}^B(t_0)=v_0\!\ \vec{\imath}=\vec{v}^B\\ \\ \displaystyle \overrightarrow{OC}=\vec{r}_C(t_0)=a\!\ \vec{\imath}\!\ +\!\ b\!\ \vec{\jmath}\mathrm{;}\qquad\vec{v}^C(t_0)=v_0\!\ \vec{\imath}=\vec{v}^C\\ \\ \displaystyle \overrightarrow{OA}=\vec{r}_A(t_0)=b\!\ \vec{\jmath}\!\ +\!\ c\!\ \vec{k}\mathrm{;}\qquad\vec{v}^A(t_0)=v_y^A\!\ \vec{\jmath}\!\ +\!\ v_z^A\!\ \vec{k}=\vec{v}^A\end{array}$

Para determinar las compenentes desconocidas de la velocidad del vértice $A$ exigimos la equiproyectividad de las velocidades instantáneas de los tres vértices:

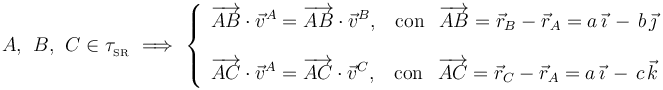
$A\mathrm{,}\;\;B\mathrm{,}\;\;C\in\tau_{{}_\mathrm{SR}}\; \Longrightarrow \;\left\{\begin{array}{l}\displaystyle \overrightarrow{AB}\cdot\vec{v}^A=\overrightarrow{AB}\cdot\vec{v}^B\mathrm{,}\quad\mathrm{con}\;\;\,\overrightarrow{AB}=\vec{r}_B-\vec{r}_A=a\!\ \vec{\imath}\!\ -\!\ b\!\ \vec{\jmath} \\ \\ \displaystyle \overrightarrow{AC}\cdot\vec{v}^A=\overrightarrow{AC}\cdot\vec{v}^C\mathrm{,}\quad\mathrm{con}\;\;\,\overrightarrow{AC}=\vec{r}_C-\vec{r}_A=a\!\ \vec{\imath}\!\ -\!\ c\!\ \vec{k}\end{array}\right.$

De la primera condición se obtiene...

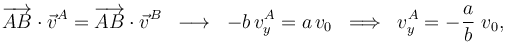
$\overrightarrow{AB}\cdot\vec{v}^A=\overrightarrow{AB}\cdot\vec{v}^B\;\; \longrightarrow \;\; -b\!\ v_y^A=a\!\ v_0\;\; \Longrightarrow \;\; v_y^A=-\frac{a}{b}\ v_0\mathrm{,}\;\;$

... y de la segunda...

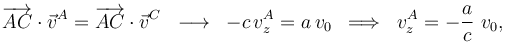
$\overrightarrow{AC}\cdot\vec{v}^A=\overrightarrow{AC}\cdot\vec{v}^C\;\; \longrightarrow \;\; -c\!\ v_z^A=a\!\ v_0\;\; \Longrightarrow \;\; v_z^A=-\frac{a}{c}\ v_0\mathrm{,}\;\;$

Por tanto, la velocidad del vértice $A$ en el instante $t 0$ es:

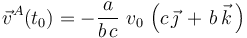
$\vec{v}^A(t_0)=-\frac{a}{b\!\ c}\ v_0\!\ \left(c\!\ \vec{\jmath}\!\ +\!\ b\!\ \vec{k}\!\ \right)$

2.2 Vector rotación instantánea

Como sabemos, el teorema de Chasles establece que dado un sólido rígido en movimiento, en cada instante de tiempo existe un único vector 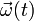$\vec{\omega}(t)$ para todo el campo de velocidades, denominado vector rotación instantánea, que relaciona las velocidades instantáneas en cualquier par de puntos:

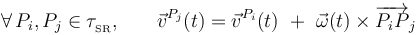
$\forall\, P_i\mathrm{,}\!\ P_j\in \tau_{{}_\mathrm{SR}}\mathrm{,}\qquad \vec{v}^{P_j}(t)=\vec{v}^{P_i}(t)\ +\ \vec{\omega}(t)\times\overrightarrow{P_iP}_j$

En el sistema bajo estudio y en el instante considerado, existirá un vector 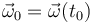$\vec{\omega}_0=\vec{\omega}(t_0)$ que relaciona las velocidades instantáneas de los puntos del triángulo rígido y, en particular, de sus vértices. Si tenemos en cuenta que las velocidades de los vértices $B$ y $C$ se igualan en el instante $t 0$ y que la del vértice $A$ es distintas, podemos asegurar que el vector rotación instantánea es no nulo y su dirección es la del segmento $\overrightarrow{BC}$ :

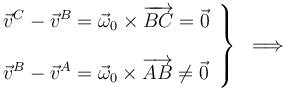
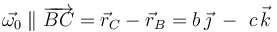
$\left.\begin{array}{l}\displaystyle \vec{v}^C-\vec{v}^B= \vec{\omega}_0\times\overrightarrow{BC}=\vec{0}\\ \\ \displaystyle \vec{v}^B-\vec{v}^A= \vec{\omega}_0\times\overrightarrow{AB}\neq\vec{0} \end{array}\right\}\;\; \Longrightarrow$ $\vec{\omega_0}\; \|\;\overrightarrow{BC}=\vec{r}_C-\vec{r}_B=b\!\ \vec{\jmath}\ - \ c\!\ \vec{k}$

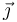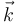Por tanto, la expresión analítica cartesiana del vector rotación en en instante $t 0$ sólo debe tener componentes en las direcciones de los unitarios $\vec{\jmath}\,$ y $\, \vec{k}$ , y éstas deben tener distinto signo:

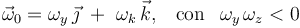
$\vec{\omega}_0=\omega_y\!\ \vec{\jmath}\ +\ \omega_k\!\ \vec{k}\mathrm{,}\quad\mathrm{con}\;\;\,\omega_y\!\ \omega_z<0$

Para determinar su valor utilizamos, por ejemplo, la segunda de las anteriores relaciones vectoriales:

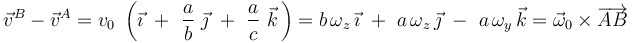
$\vec{v}^B-\vec{v}^A=v_0\ \left(\vec{\imath}\ +\ \frac{a}{b}\ \vec{\jmath}\ +\ \frac{a}{c}\ \vec{k}\!\ \right)=b\!\ \omega_z\!\ \vec{\imath}\ +\ a\!\ \omega_z\!\ \vec{\jmath}\ -\ a\!\ \omega_y\!\ \vec{k}=\vec{\omega}_0\times\overrightarrow{AB}$

... obteniéndose:

$\left.\begin{array}{l}\displaystyle \omega_z=\frac{v_0}{b}\\ \\ \displaystyle\omega_y=-\frac{v_0}{c} \end{array}\right\}\; \Longrightarrow$ $\vec{\omega}_0=\vec{\omega}(t_0)=-\frac{v_0}{b\!\ c}\ \left(b\!\ \vec{\jmath}\ -\ c\!\ \vec{k}\!\ \right)$

Movimiento instantáneo de triángulo rígido con vértices en planos ortogonales, F1 GIA (Ene, 2018)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidades de los vértices del triángulo en un instante

2.2 Vector rotación instantánea

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES