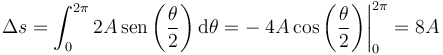Movimiento cicloidal (CMR)
De Laplace
Contenido |
1 Enunciado
Un punto exterior de una rueda que rueda sin deslizar describe una cicloide
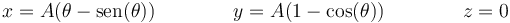
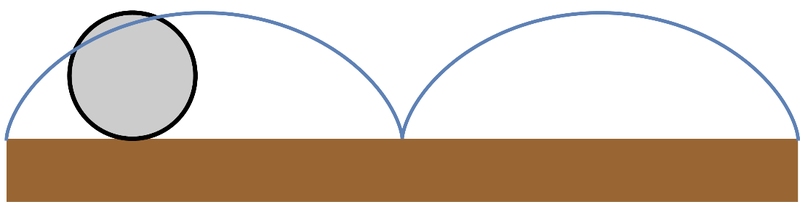
- Determine la velocidad y aceleración de la partícula en función de θ y sus derivadas respecto al tiempo. ¿Cuánto valen
 y
y  en el momento en que el punto se halla en lo más alto de la rueda?
en el momento en que el punto se halla en lo más alto de la rueda?
- Halle la aceleración tangencial y normal.
- Calcule la posición de los centros de curvatura.
- Halle la distancia recorrida por el punto cuando la rueda da una vuelta completa.
2 Velocidad y aceleración
Las componentes cartesianas de la velocidad las hallamos aplicando la regla de la cadena
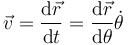
Separando por componentes
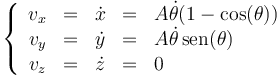
Derivando de nuevo obtenemos la aceleración. Por componentes:
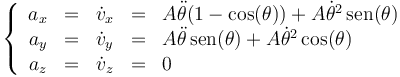
El punto más alto del movimiento se encuentra cuando y es máximo. Esto ocurre cuando cos(θ) = − 1, en que y = 2. lo cual sucede cuando cos(θ) = π. Para este valor
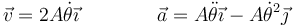
3 Aceleración tangencial y normal
3.1 Aceleración tangencial
Para hallar la aceleración tangencial podemos hacerlo derivando la la rapidez del movimiento
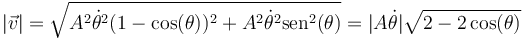
Este resultado se simplfica empleando las relaciones trigonométricas

lo que nos deja la rapidez en
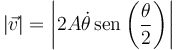
donde las barras son necesarias, ya que puede ocurrir que alguno de los factores sea negativo.
Si tenemos la rapidez podemos hallar la aceleración tangencial derivando respecto al tiempo. Si suponemos, por simplicidad, que todos los factores son positivos (como ocurriría en una rueda que va avanzando)
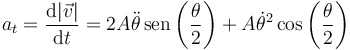
Otra forma es, primero calculamos el vector tangente (suponiendo que los factores de la rapidez son positivos)
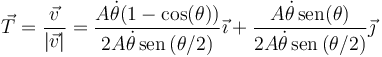
que, con las relaciones trigonométricas anteriores, queda
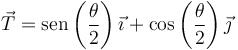
y ahora proyectamos la aceleración en la dirección del vector tangente
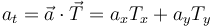
lo que nos da
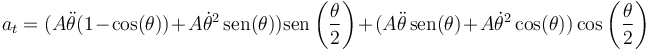
Agrupamos términos del mismo tipo y queda
- En
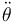
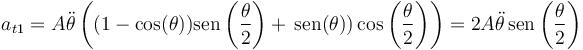
- (se ha usado la fórmula del seno de una diferencia).
- En
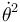
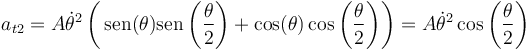
- (se ha usado la fórmula del coseno de una diferencia).
Sumando los dos términos
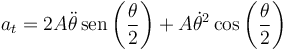
que, por supuesto, coincide con lo que habíamos obtenido derivando.
La aceleración tangencial, como vector, la obtenemos multiplicando por el vector tangente.
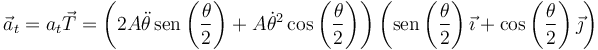
que equivale a
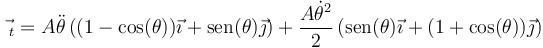
3.2 Aceleración normal
Aunque existen caminos más cortos, si seguimos el proceso estándar, calculamos la aceleración normal restando la tangencial de la completa

que se reduce a
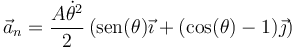
En módulo, esta componente vale, operando igual que con la rapidez,
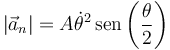
y, para el vector normal
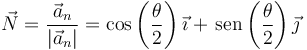
4 Centros de curvatura
4.1 Radio de curvatura
El radio de curvatura en cada instante lo obtenemos de la rapidez y la aceleración normal
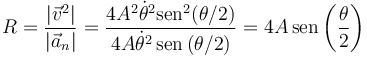
5 Distancia recorrida
La distancia recorrida la calculamos integrando la rapidez respecto al tiempo
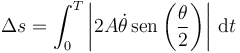
Al dar una vuelta, θ varía de 0 a 2π y por tanto θ/2 varía de 0 a π. En este rango el seno es siempre positivo. Por otro lado

así que la distancia que queremos calcular es