Flujo de energía alrededor de un dipolo magnético cargado
De Laplace
Contenido |
1 Enunciado
Suponga un pequeño imán (modelable por un dipolo magnético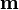 
) en cuyo interior hay una carga eléctrica q.
- Calcule las densidades de energía eléctrica y magnética en el sistema.
- Determíne el vector de Poynting en cada punto del espacio. ¿Cómo se interpreta en este sistema el flujo de energía?
- Compruebe que se verifica el teorema de Poynting en forma diferencial
2 Introducción
En este sistema tenemos un campo eléctrico y magnético estacionarios.
El campo eléctrico es el de una carga puntual
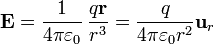
El campo magnético es el de un dipolo magnético
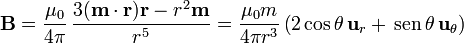
3 Energía almacenada
3.1 Eléctrica
La densidad de energía eléctrica en el espacio que rodea a la carga es
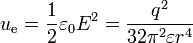
Esta energía se distribuye por igual en todas las direcciones alrededor de la carga
3.2 Magnética
La densidad de energía magnética es, del mismo modo
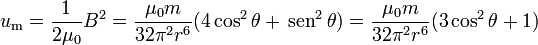
Esta energía no se distribuye de forma isótropa, sino que su densidad es mayor en el eje del dipolo (donde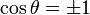 
) y menor en el plano ecuatorial.
4 Vector de Poynting
El vector de Poynting lo obtenemos multiplicando vectorialmente los campos eléctrico y magnético
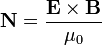
lo que da, en forma general
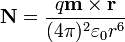
y empleando coordenadas esféricas
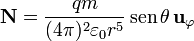
Lo interesante de este resultado es que no es nulo. En una situación de campos estáticos, sería de esperar que hubiera energía electromagnética almacenada pero no que haya un flujo de energía, que usualmente se asocia a fenómenos dinámicos como una onda plana o la radiación de una antena.
¿De dónde a dónde fluye esta energía? La expresión resultante nos muestra que el vector de Poynting va en la dirección acimutal, esto es, que el flujo de energía se produce de forma circular, dando vueltas en torno al dipolo cargado. Este resultado sí es compatible con el hecho de que la situación sea estacionaria, ya que en ningún punto se produce acumulación o disminución en la densidad de energía almacenada.
5 Teorema de Poynting
El teorema de Poynting en forma diferencial se escribe
- En este sistema no hay corriente alguna, por lo que la potencia desarrollada se anula
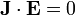
- La energía almacenada es estacionaria, por lo que su derivada temporal es nula
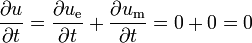
- Para que se cumpla el teorema, el vector de Poynting debe ser un campo solenoidal, como de hecho ocurre. Aplicando la expresión de la divergencia en esféricas y que el vector de Poynting es puramente acimutal:
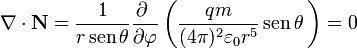
El que este vector sea solenoidal nos expresa de nuevo el que no hay flujo neto de energía. En cada punto y en cada volumen, la energía que entra por un lado, sale por otro.
