Energía magnética (GIE)
De Laplace
Contenido |
1 Corrientes de Foucault
Cuando se tiene un material metálico en el interior de un campo magnético variable en el tiempo se inducen corrientes de acuerdo con la ley de Faraday. En el caso de una espira, el resultado es una corriente a lo largo de ella, pero si tenemos un bloque de material lo suficientemente grande, pueden formarse líneas de corriente dentro del propio material. Estas corrientes describen circunferencias y otras curvas cerradas que no salen del material. Estas corrientes inducidas interiores se denominan corrientes de Foucault (o corrientes de remolino, “eddy currents” en inglés)
Podría pensarse que estas corrientes, al no fluir a lo largo de un circuito, no tienen efecto alguno, pero no es así. En primer lugar, generan calor por efecto Joule. Este calor es a menudo indeseable, ya que produce el calentamiento de partes de un sistema y debe ser desalojado. Un caso importante donde esto osucrre es en los núcleos de los transformadores. En un transformador las dos bobinas se montan sobre un núcleo de hierro. El campo magnético de las bobinas induce corrientes en el interior del hierro, calentándolo.
Para modelar este comportamiento se puede considerar un núcleo cilíndrico metálico a lo largo del cual existe un campo magnético variable en el tiempo de forma alterna
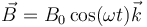
Dividiendo el volumen en espiras circulares y hallando la corriente inducida y, a partir de esta, la potencia disipada en cada una y la potencia total disipada (integrando todo el volumen) obtenemos un valor promedio
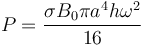
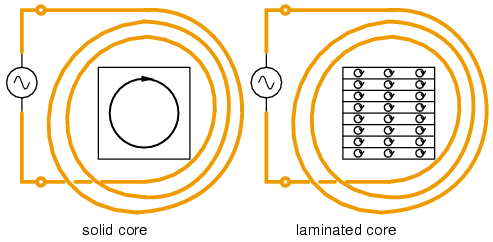
Este resultado muestra que las pérdidas aumentan como la cuarta potencia del radio. Esto implica que para un núcleo que tenga el doble de radio que otro, las pérdidas son 16 veces mayores. Para reducir este efecto los núcleos de los transformadores son laminados, ya que así se reduce el radio de cada capa.
No siempre este calor es indeseado. En las cocinas de inducción se emplea el mismo principio para calentar la comida.
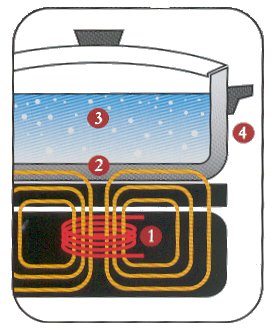
2 Frenos magnéticos
Como ilustración del efecto de las fuerzas magnéticas en el balance energético consideremos el caso de una espira que penetra en un campo magnético
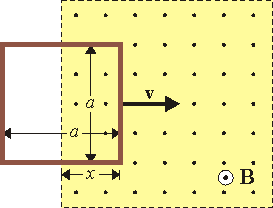
Supongamos en primer lugar que la espira se mueve con velocidad constante  . En este caso, de acuerdo con la ley de Faraday, en la espira se induce una corriente (supuesta en sentido antihorario)
. En este caso, de acuerdo con la ley de Faraday, en la espira se induce una corriente (supuesta en sentido antihorario)
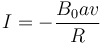
siendo R la resistencia de la espira. Ahora bien, la presencia de esta corriente produce calor por efecto Joule, siendo la potencia disipada
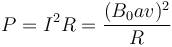
Esta potencia eléctrica que entra se emplea en un aumento de la energía interna (aumento de temperatura de la espira) o se escapa en forma de calor. Si aquí aplicamos el primer principio de la termodinámica, podemos preguntarnos ¿de donde proviene esta energía entrante? Debe ser de una disminución de la energía total o de trabajo o calor que entran.
- De la energía total no es, pues la energía cinética permanece constante y la interna no está disminuyendo, ya que la espira no se está enfriando (al contrario se está calentando, pues parte de esa potencia sirve para aumentar la temperatura de la espira)
- Tampoco del calor que entra, pues no está entrando calor alguno en la espira
- Debemos concluir entonces que procede de trabajo que está entrando. ¿Quién realiza este trabajo?
Si la espira se mueve a velocidad constante, por la segunda ley de Newton
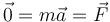
La fuerza neta sobre la espira debe ser nula. Sin embargo, sabemos que sobre una corriente rectilínea por la que circula una corriente y está dentro de un campo magnético aparece una fuerza
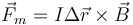
siendo 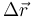 el vector de posición relativo entre los extremos de la varilla. En este caso:
el vector de posición relativo entre los extremos de la varilla. En este caso:
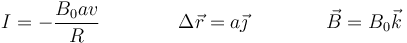
quedando la fuerza
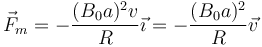
El campo magnético produce una fuerza opuesta al movimiento de la espira e intenta frenarla. Funciona como un rozamiento viscoso. Si la espira mantiene la velocidad constante es porque debe haber un agente externo empujando la espira. Alguien debe compensar la fuerza magnética de forma que
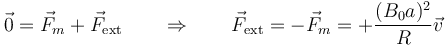
La potencia desarrollada por esta fuerza externa es
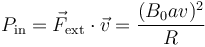
Vemos que coincide con la producción de calor por efecto Joule. Por tanto, vemos de donde sale la energía en este caso: procede del agente externo que está empujando la espira, el cual para mantener la velocidad constante debe realizar un trabajo sobre ella.
Supongamos ahora que no hay un agente externo actuando. Nadie empuja la espira. ¿De dónde sale entonces la energía? En ese caso ya no es cierto que la espira se mueva con velocidad constante, ya que no hay nadie que compense la fuerza magnética. Debe determinarse como se mueve la espira, lo que se hace en un problema. de acuerdo con la segunda ley de Newton
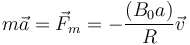
La solución de esta ecuación diferencial es una exponencial

La velocidad decae exponencialmente, lo que quiere decir que la espira se va frenando como si entrara en un fluido. τ da un tiempo típico de frenado (cuando han pasado 3 ó 4 veces τ ya velocidad es prácticamente nula). Ese tiempo de frenado depende de la masa de la espira (a mayor masa, mayor inercia y por tanto más tarda en pararse), de la resistencia (a mayor resistencia menor intensidad de corriente y menor frenado) y del campo magnético (más campo supone un mayor frenado).
Si calculamos la energía total disipada por las corrientes inducidas queda
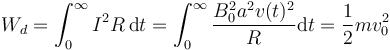
Este es el principio de los frenos magnéticos:
- El campo magnético induce unas corrientes en el material conductor
- El campo magnético actúa sobre esas mismas corrientes, disipando energía cinética y frenando al material.
La ventaja de los frenos magnéticos es que no implican fricción mecánica, que va desgastando las piezas. El inconveniente es que producen una cierta cantidad de calor que debe ser disipado.

3 Energía magnética
3.1 Energía almacenada en un circuito
En un circuito simple, que posea una autoinducción no nula, para establecer una corriente estacionaria, un generador debe realizar un trabajo extra, para vencer la f.e.m. que se le opone, de acuerdo con la ley de Lenz.
De acuerdo con la expresión para la potencia que entra en un sistema de dos terminales
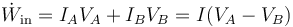
ya que la corriente I que entra por A es la misma que sale por B
A su vez, según se ve al definir la fuerza electromotriz de un generador
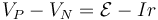
siendo P el punto por el que sale la corriente (en nuestro caso B) y N por el que entra (que sería A). Por tanto, si hay f.e.m. presente
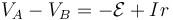
y en el caso de que sea una autoinducción la causante de la f.e.m.

por lo que la potencia que entra en el sistema en cada instante es
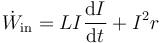
El segundo término corresponde a la energía eléctrica disipada en el sistema por efecto Joule, pero ¿qué representa el primero? Lo podemos escribir en la forma
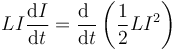
que nos dice que se trata de una de una función de estado, es decir, que representa una magnitud que se puede calcular a partir del estado del sistema y que se puede interpretar como que está almacenada, siendo recuperable.
3.2 Corriente de cierre
Para ilustrarlo consideremos un sistema sencillo formado por una fuente externa de f.e.m. 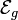 y una bobina de resistencia R y coeficiente de autoinducción L.
y una bobina de resistencia R y coeficiente de autoinducción L.
La intensidad de corriente en el circuito satisface la ecuación diferencial

Siendo su solución una que tiende asintóticamente a una corriente continua
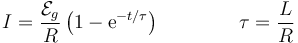
Si calculamos la potencia entregada por el generador
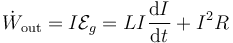
El último término es claramente la potencia disipada por efecto Joule, que debe ser aportada por el generador. Pero el generador debe realizar un trabajo adicional, debido a la presencia de la autoinducción. ¿A dónde va a parar esta energía? Si integramos durante un cierto periodo de tiempo queda
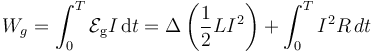
El primer término es una función de estado que depende únicamente de los valores iniciales y finales de la intensidad de corriente. Una vez que se alcanza el estado estacionario, esa cantidad no varía.
3.3 Corriente de ruptura
Podemos afirmar que esa energía está almacenada en el circuito. La demostración es sencilla. Supongamos que se cortocircuita la fuente, de manera que ya no hay nadie aportando energía. Aun así, la corriente continúa circulando un poco de tiempo, según la ecuación
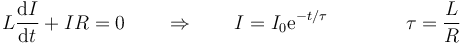
Durante este periodo transitorio final, en el que la corriente decae exponencialmente, se disipa una energía
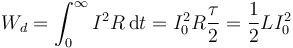
es decir, la energía que se disipa cuando ya no está la fuente es exactamente la misma que añadió la fuente en el transitorio inicial. Concluimos entonces que la energía ha estado almacenada todo el tiempo.
3.4 Energía magnética
Según esto, siempre que tengamos una autoinducción en el circuito, ésta almacena una energía magnética
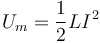
Esta energía viene a ser el análogo magnético de la energía eléctrica almacenada en un condensador
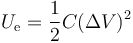
En un circuito, los condensadores almacenan energía eléctrica y las bobinas energía magnética. En un circuito LC ideal (formado solamente por un condensador y una bobina) la corriente oscila de manera que la energía eléctrica se transforma en magnética y viceversa. Viene a ser lo mismo que la transformación de energía potencial en cinética y viceversa en un oscilador armónico.
3.5 Energía almacenada en el campo magnético
Operando con las ecuaciones para el campo magnético se llega a que la energía magnética se puede calcular como la integral de volumen de una densidad
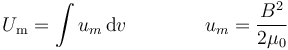
La interpretación que se hace es que la energía magnética no se almacena “en el ecircuito”, sino en el campo magnético que hay dentro de la bobina (al igual que la energía eléctrica se almacena en el campo eléctrico que hay dentro del condensador).
En un fenómeno electromagnético general, como puede ser una onda electromagnética, la energía total será la suma de las dos
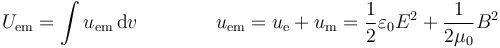

4 Potencia en un transformador
4.1 Transformador ideal
En un transformador ideal no hay pérdidas energéticas, y en el estado estacionario tampoco hay variación en la energía almacenada. Esto quiere decir que el flujo de energía a través de la frontera debe ser nulo, o, lo que es lo mismo

La energía que entra en el primario y la que sale por el secundario valen

y por tanto
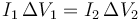
puesto que los voltajes son proporcionales, según la relación de transformación
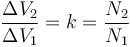
se deduce que las intensidades de corriente se hallan en la proporción inversa
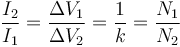
Esto implica que en un transformador ideal el voltaje se multiplica, la intensidad de corriente se divide y viceversa. Esto es lo que los hace especialmente útiles para la transmisión de energía.
Si en una casa se consume una potencia P_0 a una tensión V0 esto quiere decir que por la red debe entrar en la casa una intensidad
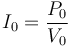
Ahora bien, si la red eléctrica que llega hasta la casa tiene una resistencia eléctrica R, esto quiere decir que para abstecer a la casa se pierde una potencia por el camino
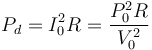
La forma de reducir esas pérdidas consiste en instalar a la salida de la central un transformador (en realidad, una sucesión de ellos) para subir el voltaje a media y a alta tensión (aumentar V0). Se transporta a alta tensión y en las proximidades de la vivienda se vuelve a bajar a media y a baja tensión.
4.2 Transformador real
La situación real es bastante más compleja ya que tenemos
- Pérdidas de energía por efecto Joule en las propias bobinas.
- Pérdidas por corrientes de Foucault en el núcleo del transformador.
- Fugas de campo magnético en el núcleo que hacen que la constante de acoplamiento no sea la unidad.
- Efectos de la carga (los dispositivos) conectados al secundario.
Todo esto hace que la eficiencia de un transformador diste de 1, lo que se manifiesta en el calentamiento de estos dispositivos, razón por la que deben ser refrigerados continuamente.





