Casos particulares de movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Introducción
2 Uniforme
3 Uniformemente acelerado
4 Armónico simple
5 Rozamiento viscoso

1 Introducción

Dentro de los movimientos rectilíneos existen infinitos casos posibles, ya que cualquier función continua puede representar el movimiento de una partícula.

Existen, no obstante, algunos casos particulares de interés:

2 Uniforme

Un movimiento rectilíneo y uniforme (M.R.U.) es aquel que posee aceleración nula en todo instante. Integrando una vez obtenemos que la velocidad es constante y que la posición varía linealmente con el tiempo

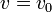
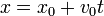
$v = v_0\,$ $x =x_0 + v_0 t\,$

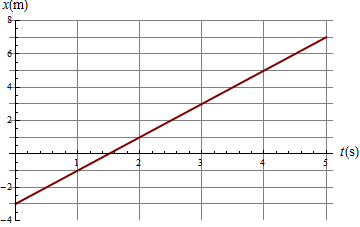
La gráfica de la posición frente al tiempo es una recta cuya pendiente es igual a la velocidad.

La gráfica de la velocidad frente al tiempo es una recta horizontal. El área bajo esta recta es un rectángulo cuya área va aumentando linealmente con el tiempo.

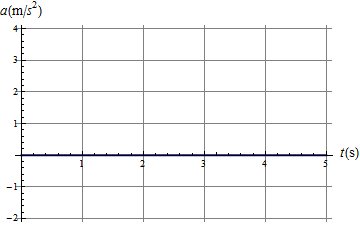
3 Uniformemente acelerado

Un movimiento rectilíneo uniformemente acelerado (M.R.U.A.) es aquel que posee una aceleración constante, $a 0$ . La integración produce una velocidad que varía linealmente y una posición que lo hace cuadráticamente

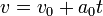
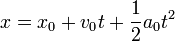
$v = v_0+a_0t\,$ $x =x_0 + v_0 t+\frac{1}{2}a_0t^2\,$

Gráficamente $x (t)$ posee forma parabólica, mientras que $v (t)$ es una recta de pendiente $a 0$

Hay que recalcar, porque es causa frecuente de errores, que esta fórmula solo se aplica al caso de que la aceleración sea constante. Si $a = a (t)$ habrá que hacer la integral y el resultado no será de esta forma.

Asimismo, si lo único que se conoce es la aceleración en un momento dado, tampoco se podrán aplicar estas fórmulas, ya que para poder integrar necesitamos conocer la aceleración durante todo un intervalo, no en un solo instante.

Un ejemplo característico de movimiento uniformemente acelerado es el de un cuerpo que cae verticalmente sin rozamiento. Si una masa se arroja verticalmente hacia arriba con velocidad inicial $v 0$ , vas ascendiendo con una rapidez cda vez menor hasta que llega a pararse en el punto de altura máxima, a partir del cual comienza a descender cada vez más rápido, llegando al suelo con la misma rapidez con que partió (pero con velocidad opuesta). La aceleración de este movimiento es constante e igual a la de la gravedad. Incluso en el punto más alto, en que la masa se para, la aceleración es distinta de cero e igual a $g$ .

La ecuación del movimiento uniformemente acelerado para este caso particular se escribe

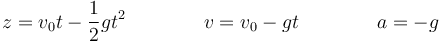
$z = v_0t-\frac{1}{2}gt^2 \qquad\qquad v = v_0-g t\qquad\qquad a = -g$

El punto de altura máxima se alcanza cuando $v = 0$ . Despejando y sustituyendo

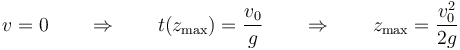
$v=0\qquad\Rightarrow\qquad t(z_\mathrm{max})= \frac{v_0}{g}\qquad\Rightarrow\qquad z_\mathrm{max}=\frac{v_0^2}{2g}$

siendo el tiempo total de viaje

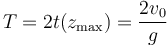
$T = 2t(z_\mathrm{max}) = \frac{2v_0}{g}$

y la distancia recorrida y la rapidez media

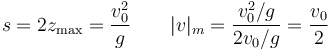
$s = 2z_\mathrm{max} = \frac{v_0^2}{g}\qquad |v|_m = \frac{v_0^2/g}{2v_0/g} = \frac{v_0}{2}$

En el caso del movimiento uniformemente acelerado se cumple la relación

$v^2 - v_0^2 = 2a_0(x-x_0)\quad\Rightarrow\quad a_0 = \frac{v^2-v_0^2}{2(x-x_0)}$

Esta expresión permite hallar la aceleración si lo que se conoce es la velocidad en dos puntos de posición conocida y se sabe que la aceleración es constante.

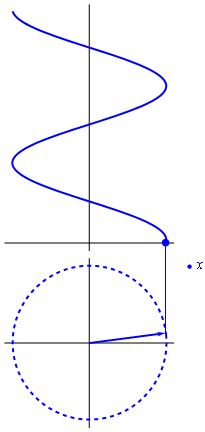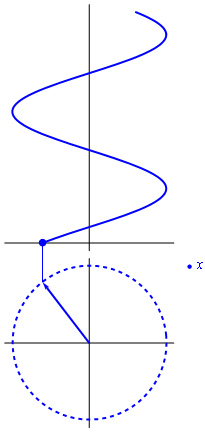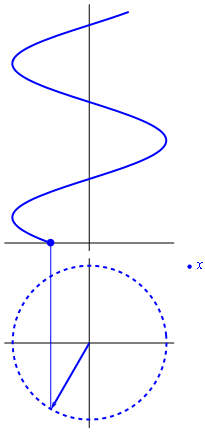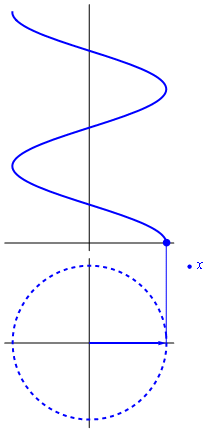
4 Armónico simple

4.1 Definición

El movimiento armónico simple (M.A.S.) es un caso particular de movimiento rectilíneo, caracterizado por la ecuación de movimiento

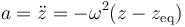
$a = \ddot{z} = -\omega^2(z-z_\mathrm{eq})$

siendo $ω$ una constante de proporcionalidad (que tiene dimensiones de inversa de tiempo) y $z eq$ otra constante, conocida como posición de equilibrio. En la mayoría de las situaciones se define la elongación como la distancia (con signo) respecto a la posición de equilibrio $x = z - z eq$ y reducir la ecuación a

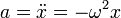
$a = \ddot{x} = -\omega^2x$

4.2 Solución y propiedades del M.A.S.

La solución de esta ecuación diferencial debe ser una función cuya segunda derivada sea proporcional a ella misma cambiada de signo. Las funciones que verifican esto son los senos y los cosenos.

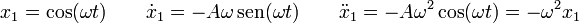
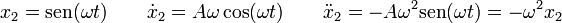
$x_1 = \cos(\omega t)\qquad \dot{x}_1 = -A\omega\,\mathrm{sen}(\omega t)\qquad\ddot{x}_1 = -A\omega^2\cos(\omega t) = -\omega^2x_1$ $x_2 = \mathrm{sen}(\omega t)\qquad \dot{x}_2 = A\omega\cos(\omega t)\qquad\ddot{x}_2 = -A\omega^2\mathrm{sen}(\omega t) = -\omega^2x_2$

La expresión general de un posible desplazamiento que verifique esta ecuación es una combinación de estas dos soluciones

$x = c_1\cos(\omega t) + c_2\,\mathrm{sen}(\omega t)$

con $c 1$ y $c 2$ dos constantes que se pueden deducir de la posición y velocidad iniciales. Derivando dos veces, se comprueba que esta función también verifica la ecuación del oscilador armónico.

Imponiendo que la posición inicial valga $x 0$ obtenemos

$x_0=x(t=0) = c_1\overbrace{\cos(0)}^{=1}+c_2\overbrace{\mathrm{sen}(0)}^{=0}=c_1\qquad\Rightarrow\qquad c_1 = x_0$

Derivando e imponiendo que la velocidad inicial valga $v 0$

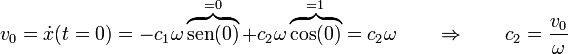
$v_0=\dot{x}(t=0) = -c_1\omega\overbrace{\mathrm{sen}(0)}^{=0}+c_2\omega\overbrace{\cos(0)}^{=1}=c_2\omega\qquad\Rightarrow\qquad c_2 = \frac{v_0}{\omega}$

y queda la solución en función de las condiciones iniciales

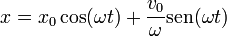
$x = \displaystyle x_0\cos(\omega t) + \frac{v_{0}}{\omega}\mathrm{sen}(\omega t)$

Podemos combinar las dos funciones en una sola si definimos las cantidades $A$ y $β$ tales que

$c_1 = A\cos(\beta)\qquad c_2 = -A\,\mathrm{sen}(\beta)$

de manera que la solución general puede reescribirse como

$x = A\cos(\omega t +\beta)\,$

siendo $A$ y $β$ dos constantes que también se pueden calcular a partir de la posición y la velocidad iniciales. La equivalencia entre las dos expresiones se demuestra desarrollando el coseno de la diferencia.

En función de las condiciones iniciales queda

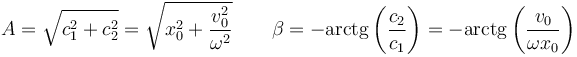
$A=\sqrt{c_1^2+c_2^2}=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}\qquad \beta = -\mathrm{arctg}\left(\frac{c_2}{c_1}\right)=-\mathrm{arctg}\left(\frac{v_0}{\omega x_0}\right)$

La velocidad y la aceleración instantáneas se calculan derivando la expresión de $x (t)$ :

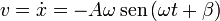
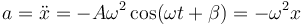
$v = \dot{x} = -A\omega\,\mathrm{sen}\,(\omega t+\beta)$ $a = \ddot{x}=-A\omega^2\cos(\omega t+\beta)=-\omega^2 x\,$

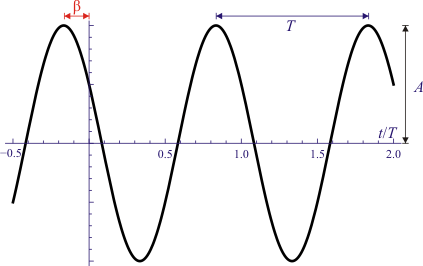
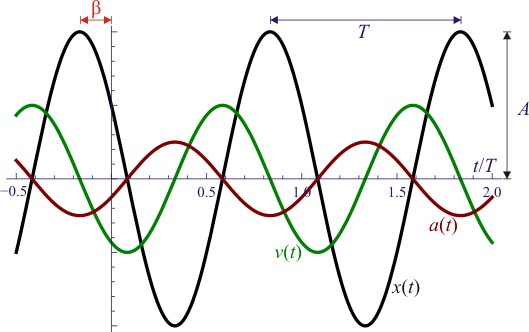
Si representamos la posición a lo largo del eje X como función del tiempo obtenemos una función periódica

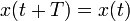
$x(t+T) = x(t)\,$

con $T$ el periodo de oscilación. La forma de la función es sinusoidal. Este movimiento se caracteriza por los siguientes variables y constantes:

Elongación, $x (t)$: es la posición instantánea, considerada como distancia (con signo) respecto a la posición central del movimiento.
Fase, $φ = ω t + β$: Indica en que punto del ciclo se encuentra el sistema. Para un periodo varía entre 0 y 2π rad.
Amplitud, $A$: es la máxima elongación del movimiento. Se mide en m en el SI.
Frecuencia angular, $ω$: En el SI se mide en rad/s.
Periodo, $T$: Es el intervalo necesario para una oscilación completa. Se calcula a partir de la frecuencia angular como

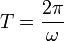
$T = \frac{2\pi}{\omega}$

En el SI el periodo se mide en s.

Frecuencia natural, $f$: mide el número de oscilaciones que el sistema realiza en la unidad de tiempo. Es la inversa del periodo

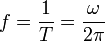
$f=\frac{1}{T}=\frac{\omega}{2\pi}$

En el SI se mide en hercios, Hz, equivalentes a 1 ciclo/s o simplemente a 1 s⁻¹.

Constante de fase, $β$: También llamada fase inicial. Nos da el valor de la fase en el instante inicial (t=0). Gráficamente es proporcional a la distancia (medida en radianes) entre el punto de máxima elongación y el instante inicial

La velocidad y la aceleración de este movimiento son también funciones oscilatorias, con el mismo periodo pero desfasadas, un cuarto de periodo la velocidad y medio periodo la aceleración. En un periodo de oscilación, cuando la elongación es máxima, la velocidad es nula y la aceleración es máxima (pero de signo contrario a la elongación). En el punto central la elongación y la aceleración son nulas, mientras que la velocidad es máxima.

El valor extremo de la velocidad corresponde a una fase de $π / 2$ o $3π / 2$

$v(t) = \dot{x}=-A\omega\,\mathrm{sen}(\omega t +\beta)\qquad\Rightarrow\qquad |v|_\mathrm{max} =A\omega = \sqrt{v_0^2+\omega^2x_0^2}$

El valor máximo de la aceleración lo da la propia ecuación de movimiento del oscilador armónico

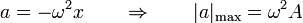
$a = -\omega^2x\qquad\Rightarrow\qquad |a|_\mathrm{max} = \omega^2A$

4.3 Estudio empleando variable compleja

Existe una forma más elegante de expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas

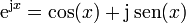
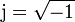
$\mathrm{e}^{\mathrm{j}x} = \cos(x)+\mathrm{j}\,\mathrm{sen}(x)$ $\mathrm{j}=\sqrt{-1}$

o, equivalentemente,

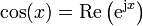
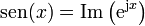
$\cos(x) = \mathrm{Re}\left(\mathrm{e}^{\mathrm{j}x}\right)$ $\mathrm{sen}(x) = \mathrm{Im}\left(\mathrm{e}^{\mathrm{j}x}\right)$

4.4 Vectores rotatorios

Si consideramos que el exponente en la fórmula de Euler es proporcional al tiempo, el resultado es un vector rotatorio en el plano complejo

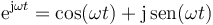
$\mathrm{e}^{\mathrm{j}\omega t} = \cos(\omega t)+\mathrm{j}\,\mathrm{sen}(\omega t)$

La parte real de este número complejo rotatorio, esto es, su proyección sobre el eje de abscisas, representa una oscilación cosenoidal. La parte imaginaria oscila igualmente, pero como un seno, esto es, desfasada un cuarto de periodo.

4.5 Amplitudes complejas (fasores)

La solución general del movimiento armónico simple, en función de las condiciones iniciales, es

$x = c_1\cos(\omega t) + c_2\,\mathrm{sen}(\omega t)=x_0\cos(\omega t) + \frac{v_0}{\omega}\mathrm{sen}(\omega t)$

y, en función de la amplitud y la fase

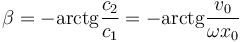
$x = A\cos(\omega t+\beta)\,$ $A=\sqrt{a^2+b^2}=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$ $\beta=-\mathrm{arctg}\frac{c_2}{c_1}=-\mathrm{arctg}\frac{v_0}{\omega x_0}$

Aplicando la fórmula de Euler a la expresión anterior

$x = A \cos(\omega t + \beta) = \mathrm{Re}\left(A \mathrm{e}^{\mathrm{j}(\omega t + \beta)}\right) = \mathrm{Re}\left(\hat{x}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde

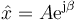
$\hat{x}=A\mathrm{e}^{\mathrm{j}\beta}$

es la llamada amplitud compleja o fasor de la variable $x$ . El movimiento armónico simple se puede ver entonces como la proyección sobre el eje real de un vector que gira en el plano complejo y cuyo valor en el instante $t = 0$ es la amplitud compleja 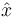$\hat{x}$ .

Se define entonces, en general, la amplitud compleja o fasor 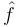$\hat{f}$ de una cantidad oscilante $f (t)$ como aquel número complejo constante que cuando se multiplica por $e jω t$ y se halla la parte real del producto, resulta la cantidad $f (t)$ .

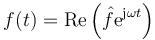
$f(t) = \mathrm{Re}\left(\hat{f}\mathrm{e}^{\mathrm{j}\omega t}\right)$

Este número complejo tiene por módulo la amplitud de las oscilaciones y por argumento la constante de fase

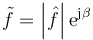
$\tilde f = \left|\hat{f}\right|\mathrm{e}^{\mathrm{j}\beta}$

Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor de la posición

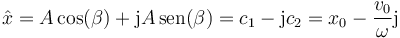
$\hat{x}= A\cos(\beta)+\mathrm{j}A\,\mathrm{sen}(\beta)=c_1-\mathrm{j}c_2=x_0-\frac{v_0}{\omega}\mathrm{j}$

esto es, la amplitud compleja queda completamente determinada por las condiciones iniciales del movimiento.

4.6 Velocidad en un MAS

La gran ventaja de la definición de los fasores es que simplifican enormemente las derivadas e integrales.

Si derivamos la expresión fasorial obtenemos la velocidad instantánea de una partícula en un MAS

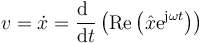
$v = \dot{x}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathrm{Re}\left(\hat{x}\mathrm{e}^{\mathrm{j}\omega t}\right)\right)$

La derivada de una parte real es la parte real de la derivada, y 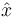$\hat{x}$ es una cantidad constante, por lo que

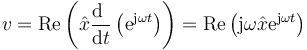
$v = \mathrm{Re}\left(\hat{x}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathrm{e}^{\mathrm{j}\omega t}\right)\right) = \mathrm{Re}\left(\mathrm{j}\omega\hat{x}\mathrm{e}^{\mathrm{j}\omega t}\right)$

Esto es, la velocidad también se puede escribir en forma fasorial

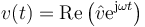
$v(t) = \mathrm{Re}\left(\hat{v}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde

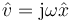
$\hat{v}=\mathrm{j}\omega \hat{x}$

es decir, para calcular el fasor de la derivada de una magnitud, solo necesitamos multiplicar el fasor de dicha magnitud por $jω$ . El uso de fasores transforma las derivadas en multiplicaciones.

En función de las condiciones iniciales el fasor de la velocidad es

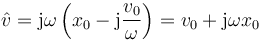
$\hat{v}=\mathrm{j}\omega\left(x_0-\mathrm{j}\frac{v_0}{\omega}\right) = v_0+\mathrm{j}\omega x_0$

Podemos comprobar que efectivamente este fasor produce la velocidad como función del tiempo

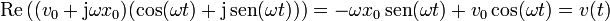
$\mathrm{Re}\left((v_0+\mathrm{j}\omega x_0)(\cos(\omega t)+\mathrm{j}\,\mathrm{sen}(\omega t))\right)=-\omega x_0\,\mathrm{sen}(\omega t)+v_0\cos(\omega t) = v(t)$

El resultado es la derivada temporal de la posición.

En el plano complejo, el fasor de la velocidad está girado 90° respecto al de la posición, como resultado de la multiplicación por la unidad imaginaria.

4.7 Aceleración en un MAS

La misma regla algebraica la podemos aplicar al cálculo de la aceleración. Su fasor será igual al de la velocidad multiplicado por $jω$

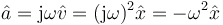
$\hat{a}=\mathrm{j}\omega\hat{v}=(\mathrm{j}\omega)^2\hat{x}=-\omega^2\hat{x}$

Gráficamente el fasor de la aceleración está girado 90° respecto al de la velocidad y por tanto posee sentido opuesto al de la posición.

La regla inversa a la de la derivación se aplica a la hora de integrar. Si se sabe que tanto una magnitud como su primitiva son funciones oscilantes, el fasor de la primitiva es simplemente el fasor de la magnitud dividido por $jω$ . Así

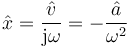
$\hat{x}=\frac{\hat{v}}{\mathrm{j}\omega}=-\frac{\hat{a}}{\omega^2}$

5 Rozamiento viscoso

Tal como se ve en los temas de Dinámica, una forma común de rozamiento es el llamado rozamiento viscoso, que ocurre cuando una partícula se mueve en el interior de un fluido. En un modelo sencillo de este rozamiento, puede suponerse que es proporcional a la velocidad (cuanto más rápido vaya la partícula, mayor es la oposición que encuentra). Si tenemos una partícula que comienza a moverse en un medio viscoso, por ejemplo, un proyectil que penetra en el agua, su movimiento verifica

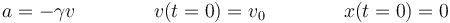
$a = -\gamma v\qquad\qquad v(t=0) = v_0\qquad\qquad x(t=0) = 0$

siendo γ una constante.

Nuestro objetivo es determinar cómo se mueve la partícula como función del tiempo $x = x (t)$ . Esto es una ecuación diferencial, que relaciona la derivada de una función con la propia función. Existen diferentes formas de integrar esta ecuación.

Una de ellas consiste en observar que ambos miembros representan una derivada respecto al tiempo,

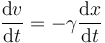
$\frac{\mathrm{d}v}{\mathrm{d}t} = -\gamma\frac{\mathrm{d}x}{\mathrm{d}t}$

con lo que puede ser integrada una vez respecto al tiempo

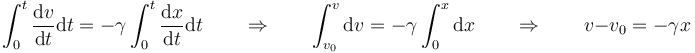
$\int_0^t \frac{\mathrm{d}v}{\mathrm{d}t}\mathrm{d}t = -\gamma\int_0^t\frac{\mathrm{d}x}{\mathrm{d}t}\mathrm{d}t\qquad\Rightarrow\qquad \int_{v_0}^v \mathrm{d}v = -\gamma\int_0^x\mathrm{d}x\qquad\Rightarrow\qquad v - v_0 = -\gamma x$

Despejando

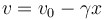
$v = v_0 -\gamma x\,$

Esta ecuación nos da la velocidad como función de la posición, que ya sabemos como integrar

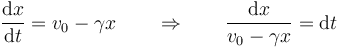
$\frac{\mathrm{d}x}{\mathrm{d}t} = v_0-\gamma x \qquad\Rightarrow\qquad \frac{\mathrm{d}x}{v_0-\gamma x} = \mathrm{d}t$

Integrando cada miembro

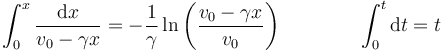
$\int_0^x \frac{\mathrm{d}x}{v_0-\gamma x} = -\frac{1}{\gamma}\ln\left(\frac{v_0-\gamma x}{v_0}\right)\qquad \qquad \int_0^t\mathrm{d}t = t$

lo que nos da finalmente la ley horaria

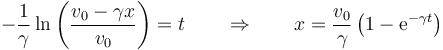
$-\frac{1}{\gamma}\ln\left(\frac{v_0-\gamma x}{v_0}\right) = t \qquad \Rightarrow\qquad x = \frac{v_0}{\gamma}\left(1-\mathrm{e}^{-\gamma t}\right)$

Siendo la velocidad y la aceleración como funciones del tiempo

$v = \dot{x}=v_0\mathrm{e}^{-\gamma t}\qquad \qquad a = \ddot{x} = -\gamma v_0\mathrm{e}^{-\gamma t}$

Nos resulta que la velocidad decae exponencialmente, y la partícula tarda (idealmente) un tiempo infinito en pararse. La partícula, no obstante, no recorre una distancia infinita, sino que se se va aproximando gradualmente a un valor límite

$x_\infty = \lim_{t\to\infty} x(t) = \frac{v_0}{\gamma}$

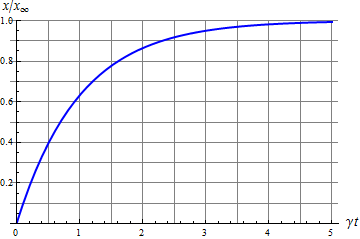
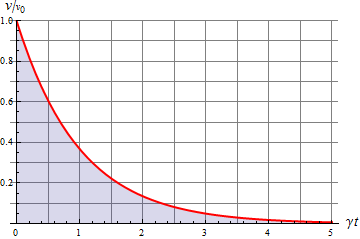
que, gráficamente, quiere decir que el área bajo la curva exponencial es finita.

Casos particulares de movimiento rectilíneo (GIE)

De Laplace

Contenido

1 Introducción

2 Uniforme

3 Uniformemente acelerado

4 Armónico simple

4.1 Definición

4.2 Solución y propiedades del M.A.S.

4.3 Estudio empleando variable compleja

4.4 Vectores rotatorios

4.5 Amplitudes complejas (fasores)

4.6 Velocidad en un MAS

4.7 Aceleración en un MAS

5 Rozamiento viscoso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES