Caso de movimiento con aceleración constante (GIOI)
De Laplace
Contenido |
1 Enunciado
Una partícula se mueve con aceleración constante, de forma que en tres instantes sucesivos ocupa las siguientes posiciones
| t(s) | 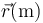
|
|---|---|

| 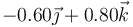
|
| 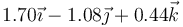
|
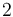
| 
|
- Halle la velocidad media en el intervalo (0 s, 2s)
- Demuestre que la velocidad instantánea inicial (en t = 0 s) vale
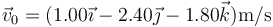 y la aceleración del movimiento en este intervalo es
y la aceleración del movimiento en este intervalo es 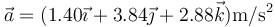
- Para el instante t = 1 s, halle:
- La velocidad, la rapidez y la aceleración instantáneas
- La aceleración tangencial y la aceleración normal (escalares)
- Los vectores del triedro de Frenet
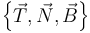
- El radio de curvatura y el centro de curvatura.
2 Velocidad media
En lo que sigue todas las cantidades con dimensiones están en las unidades fundamentales del SI: m, s o combinaciones de estos.
La velocidad media en un intervalo es el vector
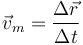
que en el intervalo (0 s,2 s) da
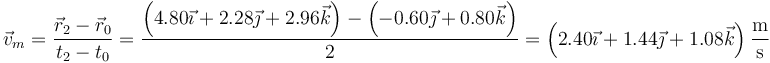
3 Velocidad inicial y aceleración
Al ser un movimiento de aceleración constante (aunque no rectilíneo; en general este tipo de movimientos es parabólico), la posición y la velocidad cumplen, en cada instante

Para determinar los coeficientes de una parábola basta imponer la posición de tres puntos. En este caso en concreto ya tenemos el coeficiente 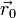 . Aplicando la ecuación del movimiento con aceleración constante a los instantes t = 1 s y t = 2s queda
. Aplicando la ecuación del movimiento con aceleración constante a los instantes t = 1 s y t = 2s queda
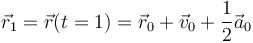
y

Sustituimos los vectores de posición y obtenemos el sistema

(este úlltimo vector ya lo habíamos calculado en el primer apartado). Restamos la primera de la segunda y hallamos la aceleración

y restando la segunda del doble de la primera hallamos la velocidad inicial
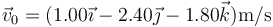
Alternativamente, como en el propio enunciado se da el resultado, es posible probarlo comprobando que en t = 1 s y en t = 2 s se obtiene el resultado dado en la tabla (hace falta sustituir en los dos instantes, no basta uno).
4 Magnitudes en t = 1s
4.1 Velocidad, rapidez y aceleración
Por tratarse de un movimiento con aceleración constante, la aceleración en t = 1 s es la misma que en t = 0 s
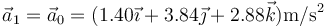
mientras que la velocidad en este instante vale

Esta velocidad instantánea coincide con la velocidad media calculada en el primer apartado. Es una cosnecuencia del movimiento con aceleración constante: en un intervalo, la velocidad media coincide con la media aritmética de las velocidades en los extremos y con la velocidad instantánea en el centro del intervalo.
La rapidez es el módulo de esta velocidad
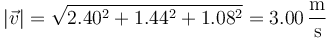
4.2 Componentes intrínsecas de la aceleración
4.2.1 Aceleración tangencial
Calculamos primero el vector tangente normalizando la velocidad
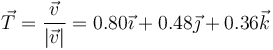
y calculamos la aceleración tangencial proyectando la aceleración sobre este vector
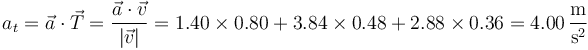
El vector aceleración tangencial será esta cantidad escalar multiplicada por el vector tangente

4.2.2 Aceleración normal
Una vez que tenemos la aceleración tangencial podemos hallar el vector aceleración normal restando los vectores
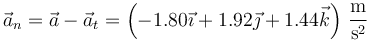
y una vez que la tenemos, calculamos su módulo para obtener la aceleración normal escalar

Alternativamente, si solo deseamos la cantidad escalar podemos hallarla empleando el teorema de Pitágoras

o con la fórmula a partir de la velocidad y la aceleración
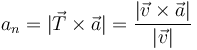
4.3 Triedro de Frenet
El vector tangente ya lo hemos calculado
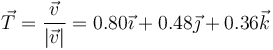
El vector normal lo podemos obtener normalizando el vector aceleración normal, si lo hemos calculado

y, una vez que tenemos estos dos vectores calculamos el binormal mediante el producto vectorial
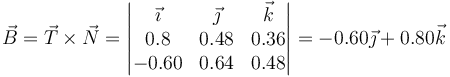
Alternativamente, podemos hallar en primer lugar el vector binormal como el unitario perpendicular a la velocidad y la aceleración
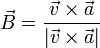
y luego el normal a partir de éste y el tangente
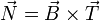
4.4 Radio y centro de curvatura
El radio de curvatura se halla a partir de la rapidez y la aceleración
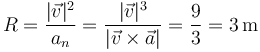
El centro de curvatura se halla prolongando el vector de posición en la dirección del vector normal






