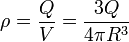Campo eléctrico y ley de Gauss (GIE)

De Laplace

Contenido

1 Concepto de electrostática
2 Campo eléctrico
3 Líneas de campo eléctrico
4 Ley de Gauss
5 Campo de cargas puntuales
- 5.1 Ley de Coulomb
6 Principio de superposición
7 Campo de una distribución de carga

1 Concepto de electrostática

La electrostática estudia los campos eléctricos y fuerzas debidas a cargas en reposo. Si además es “en el vacío” quiere decir que se consideran las cargas flotando en un espacio vacío. Puesto que más del 99% de la materia es realmente vacío, es un punto de partida adecuado. Los medios materiales (conductores o dieléctricos) pueden añadirse más tarde, como conjunto de cargas en el vacío.

En la electrostática en el vacío, los campos eléctricos son independientes dle tiempo y no hay campos magnéticos presentes. Esto reduce la ley de Lorentz para una carga puntual a solo la fuerza eléctrica

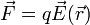
$\vec{F}=q\vec{E}(\vec{r})$

y puesto que consideramos cargas en reposo suponemos que esta fuerza se encuentra compensada por alguna otra, de forma que la resultante es nula.

2 Campo eléctrico

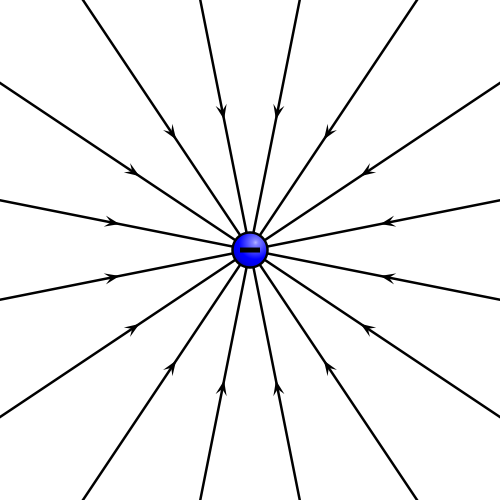
Entendemos el campo eléctrostático como una perturbación en el espacio producida por la presencia de cargas eléctricas en reposo

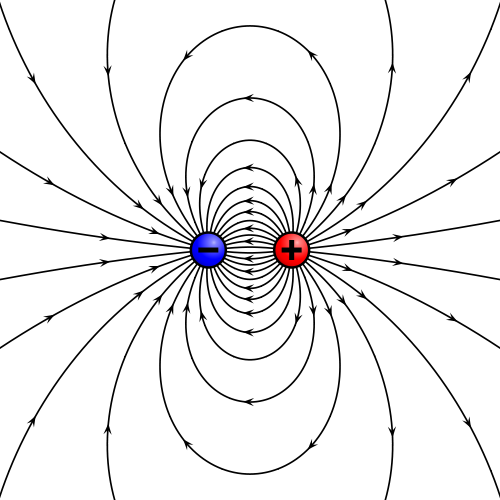
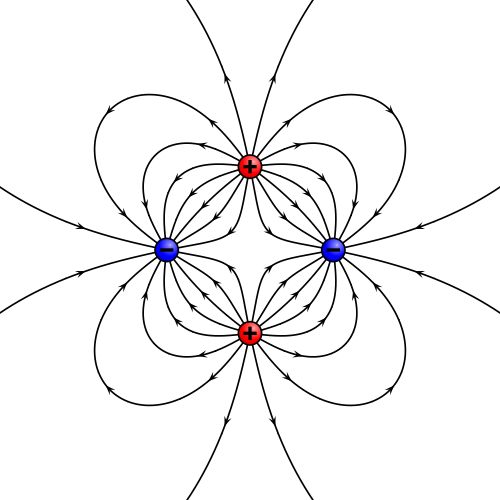
(ilustraciones obra de Geek3 para Wikipedia).

El campo es un concepto primario. No se puede describir qué es el campo eléctrico, sino solo qué efectos produce sobre otras cargas.

Puede definirse de una manera operativa, esto es, dando un procedimiento para su medida. Para ello se considera una carga muy pequeña $q 0$ y se sitúa en un campo eléctrico. Con la medida de un dinamómetro se mide la fuerza sobre ella. Se define el campo eléctrico en la posición de la carga como

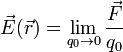
$\vec{E}(\vec{r})=\lim_{q_0\to 0}\frac{\vec{F}}{q_0}$

El límite se toma porque idealmente se considera que la carga que se coloca no debe afectar a lo que ya había, para lo cual debe ser lo más pequeña posible.

3 Líneas de campo eléctrico

Como con cualquier otro campo, se pueden trazar las líneas de campo eléctrico, como aquellas curvas que son tangentes al campo eléctrico en cada punto. Estas curvas son soluciones de la ecuación diferencial

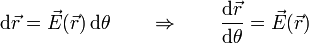
$\mathrm{d}\vec{r}=\vec{E}(\vec{r})\,\mathrm{d}\theta\qquad\Rightarrow\qquad \frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}=\vec{E}(\vec{r})$

siendo $θ$ un parámetro que nos permite etiquetar los puntos de cada curva. Estas ecuaciones diferenciales suelen ser extremadamente complejas y no poseen soluciones analíticas salvo en los casos más triviales, por lo que su solución requiere el uso de ordenadores, como en el caso de las cuatro cargas representado más arriba.

Existe casos particulares importantes:

Un campo uniforme (independiente de la posición) tiene líneas de campo que son rectas paralelas. Este es el caso del campo eléctrico en el interior de un condensador plano.

Un campo central

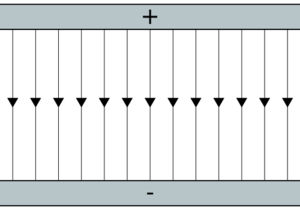
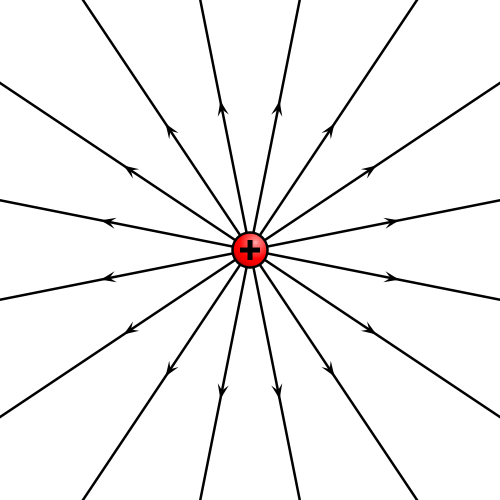
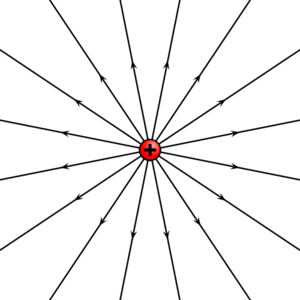
$\vec{E}(\vec{r}) = E(r)\vec{u}_r\qquad \qquad (\mbox{campo central})$

en el cual el campo es siempre puramente radial, las líneas de campo son semirrectas radiales. Este es el caso del campo de una carga puntual, positiva o negativa,

4 Ley de Gauss

Una propiedad del campo eléctrico que se desprende del trazado de sus líneas de campo es la siguiente.

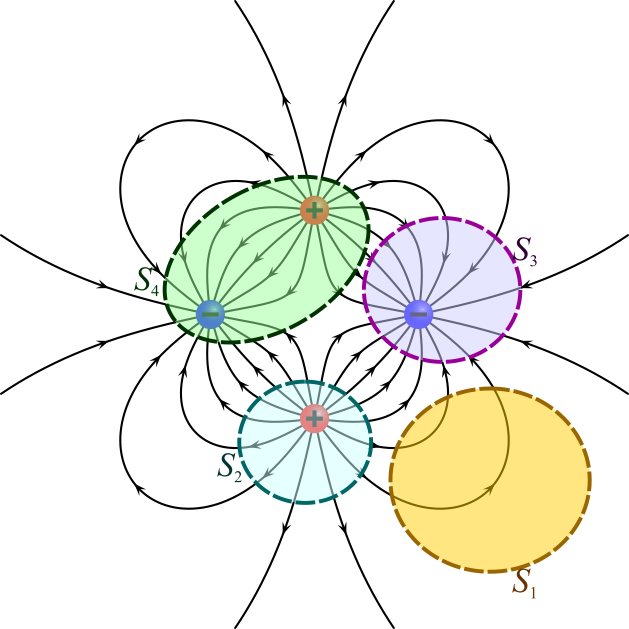
Consideremos, por ejemplo, el caso de cuatro cargas ilustrado anteriormente

Si tomamos la superficie cerrada $S 1$ , vemos que no encierra carga alguna, y que en ella hay tantas líneas de campo que entran como las que salen.
En la superficie $S 2$ , que envuelve a la carga positiva, las líneas de campo atraviesan la superficie hacia el exterior. Se dice que en esta región el campo es divergente.
En $S 3$ , en cambio, se envuelve una carga negativa y en ella el campo es convergente, atravesando las líneas de campo la superficie hacia adentro.
En $S 4$ se envuelve una carga neta 0, y vemos que en ella también hay tantas líneas que entran como que salen.

Vemos que el hecho de que las líneas atraviesen la superficie hacia afuera o hacia adentro depende de las cargas que haya en el interior, y que si es nula (bien porque no hay nada, bien porque hay tantas positivas como negativas) hay tantas que entran como que salen.

Este es un resultado general. Matemáticamente se expresa con el concepto de flujo que es una medida de cuánto campo atraviesa una superficie. La ley física que describe este fenómeno es la ley de Gauss

Ley de Gauss: El flujo del campo eléctrico a través de una superficie cerrada es proporcional a la cantidad de carga encerrada por la superficie.

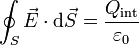
$\oint_S \vec{E}\cdot\mathrm{d}\vec{S}=\frac{Q_\mathrm{int}}{\varepsilon_0}$

Analizando cada uno de los términos de esta ecuación tenemos:

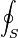
$\oint_S$: El símbolo de integral con un círculo representa la integración sobre una superficie cerrada.
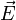
$\vec{E}$: El campo eléctrico en los puntos de la superficie. Este campo será en general función de la posición, por lo que no puede extraerse de la integral.
$\cdot$: El campo eléctrico es un vector y el diferencial de superficie también lo es. El flujo en cambio, es un número con signo. El producto escalar nos garantiza el carácter escalar del resultado.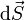; $\mathrm{d}\vec{S}$ : Cuando se integra sobre una superficie, se divide ésta en elementos de área $d S$ . Se define el vector diferencial de superficie como uno que tiene por módulo el área del elemento, por dirección la perpendicular a la superficie y por sentido el que va hacia el exterior

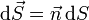
$\mathrm{d}\vec{S}=\vec{n}\,\mathrm{d}S$

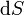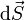(¡ojo a la diferencia entre $\mathrm{d}S\,$ y $\mathrm{d}\vec{S}$ !).

$Q int$

es la carga encerrada por la superficie. Ojo que no es toda la carga del sistema. Puede haber cargas en el exterior, que producen campo en la superficie (por ejemplo, las cuatro cargas respecto de la

S 1

anterior), pero que no están encerradas por ella. Aquí:

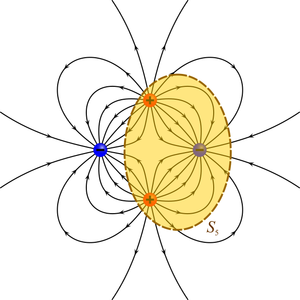
Si la carga neta encerrada es positiva: El flujo neto es hacia el exterior y el campo es divergente (caso de la superficie $S 2$ ). Esto no excluye que pueda contener cargas negativas y que haya algunas líneas de campo hacia adentro, como en la superficie $S 5$ .

Si la carga neta encerrada es negativa: El flujo neto es hacia el interior y el campo es convergente (caso de $S 3$ ).
Si la carga neta encerrada es cero: El flujo es nulo y hay tanto campo quye entra como que sale. Es importante recordar que un flujo nulo no implica un campo nulo

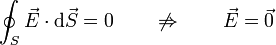
$\oint_S \vec{E}\cdot\mathrm{d}\vec{S} = 0\qquad\not\Rightarrow\qquad\vec{E}=\vec{0}$

$\varepsilon_0$: La constante de proporcionalidad es una constante universal denominada permitividad del vacío, que tiene un valor exacto

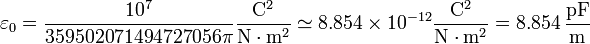
$\varepsilon_0=\frac{10^7}{359502071494727056\pi}\frac{\mathrm{C}^2}{\mathrm{N}\cdot\mathrm{m}^2}\simeq 8.854\times 10^{-12}\frac{\mathrm{C}^2}{\mathrm{N}\cdot\mathrm{m}^2} = 8.854\,\frac{\mathrm{pF}}{\mathrm{m}}$

Aunque se suele aproximar en la forma más sencilla

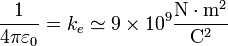
$\frac{1}{4\pi\varepsilon_0} = k_e\simeq 9\times 10^9\frac{\mathrm{N}\cdot\mathrm{m}^2}{\mathrm{C}^2}$

5 Campo de cargas puntuales

Una de las primeras aplicaciones de la ley de Gauss es la obtención del campo eléctrico creado por una carga puntual.

Por la simetría del sistema, el campo creado por una carga va a ser central

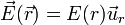
$\vec{E}(\vec{r})=E(r)\vec{u}_r$

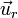siendo $r$ la distancia a la carga, $\vec{r}$ el vector de posición respecto a la carga y $\vec{u}_r$ el unitario en la dirección radial.

De acuerdo con la ley de Gauss, el flujo a través de cualquier superficie cerrada que envuelva a esta carga será el mismo. Si consideramos superficies esféricas concéntricas de radio cada vez más grande, el área de cada una crece como el cuadrado del radio, pero el flujo no cambia. Por tanto, el campo eléctrico de una carga puntual debe decaer como el cuadrado de la distancia a la carga.

Matemáticamente

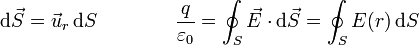
$\mathrm{d}\vec{S}=\vec{u}_r\,\mathrm{d}S\qquad\qquad \frac{q}{\varepsilon_0}=\oint_S\vec{E}\cdot\mathrm{d}\vec{S}=\oint_S E(r)\,\mathrm{d}S$

y puesto que $E (r)$ tiene el mismo valor para todos los puntos de la superficie esférica puede salir de la integral y queda

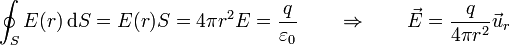
$\oint_S E(r)\,\mathrm{d}S = E(r) S = 4\pi r^2 E = \frac{q}{\varepsilon_0}\qquad\Rightarrow\qquad \vec{E}=\frac{q}{4\pi r^2}\vec{u}_r$

Más en general, si tenemos la carga en un cierto punto A, el campo que produce en un punto P es

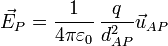
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\,\frac{q}{d_{AP}^2}\vec{u}_{AP}$

En función de los vectores de posición

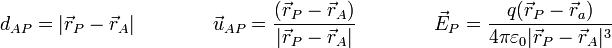
$d_{AP}=|\vec{r}_P-\vec{r}_A|\qquad\qquad \vec{u}_{AP}=\frac{(\vec{r}_P-\vec{r}_A)}{|\vec{r}_P-\vec{r}_A|}\qquad\qquad \vec{E}_P=\frac{q(\vec{r}_P-\vec{r}_a)}{4\pi\varepsilon_0|\vec{r}_P-\vec{r}_A|^3}$

El campo eléctrico de una carga puntual tiene dirección radial desde la carga y un sentido que depende del signo de ésta. Hacia afuera si es positiva y hacia adentro si es negativa.

5.1 Ley de Coulomb

Una vez que tenemos el campo eléctrico creado por una carga puntual podemos calcular la fuerza que produce sobre otra carga. Si tenemos una carga $q 1$ en 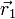$\vec{r}_1$ y situamos una carga $q 2$ en el punto 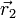$\vec{r}_2$ , la fuerza que experimenta es el producto de la carga por el campo en la posición que se encuentra

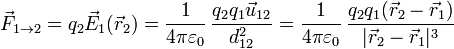
$\vec{F}_{1\to 2}= q_2\vec{E}_1(\vec{r}_2) = \frac{1}{4\pi\varepsilon_0}\,\frac{q_2q_1\vec{u}_{12}}{d_{12}^2} = \frac{1}{4\pi\varepsilon_0}\,\frac{q_2q_1(\vec{r}_2-\vec{r}_1)}{|\vec{r}_2-\vec{r}_1|^3}$

siendo 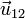$\vec{u}_{12}$ el vector unitario en la dirección de la recta que pasa por las dos cargas y en el sentido de la carga 1 a la 2. Esta es la conocida como ley de Coulomb para fuerzas entre cargas puntuales.

Dado que la fuerza es proporcional a la carga $q 2$ , si tenemos una carga $q 1$ positiva, la fuerza sobre $q 2$ será de repulsión si $q 2$ es positiva y de atracción si es negativa, aunque en los dos casos el campo de $q 1$ vaya hacia afuera.

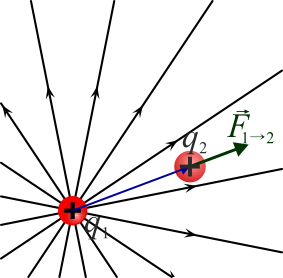
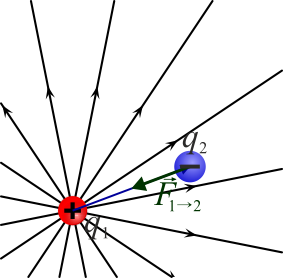
La fuerza que experimenta la carga 1 se debe a que percibe el campo de la carga 2

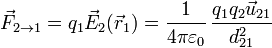
$\vec{F}_{2\to 1}= q_1\vec{E}_2(\vec{r}_1) = \frac{1}{4\pi\varepsilon_0}\,\frac{q_1q_2\vec{u}_{21}}{d_{21}^2}$

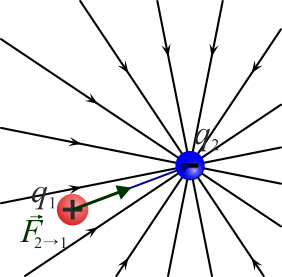
Puesto que el producto de cargas es conmutativo, la distancia es la misma en los dos casos y el vector unitario tiene la misma dirección, pero sentido opuesto al anterior, se llega a que la ley de Coulomb cumple la tercera ley de Newton

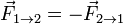
$\vec{F}_{1\to 2} = -\vec{F}_{2\to 1}$

Asimismo obtenemos las propiedades:

Cargas del mismo signo se repelen y cargas de signo opuesto se atraen.
La fuerza entre cargas puntuales en reposo es proporcional al producto de las cargas e inversamente proporcional al cuadrado de la distancia entre ellas.

La magnitud de la fuerza eléctrica es muy grande comparada con otras fuerzas de la naturaleza. Así, por ejemplo, para la fuerza entre un protón y un electrón (cargas 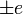$\pm e$ ) situados a una distancia $d$ tenemos

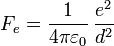
$F_e = \frac{1}{4\pi\varepsilon_0}\,\frac{e^2}{d^2}$

La fuerza gravitatoria entre las dos partículas vale en módulo, de acuerdo con la ley de Gravitación Universal

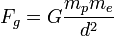
$F_g = G\frac{m_pm_e}{d^2}$

La proporción entre las dos fuerzas es independiente de la distancia entre las partículas

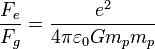
$\frac{F_e}{F_g}=\frac{e^2}{4\pi\varepsilon_0 G m_p m_p}$

Sustituyendo los valores de las cargas y masas del protón y del electrón y constantes queda

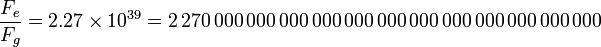
$\frac{F_e}{F_g}=2.27\times 10^{39}=2\,270\,000\,000\,000\,000\,000\,000\,000\,000\,000\,000\,000\,000$

Además, al ser esta proporción independiente de la distancia, quiere decir que la fuerza eléctrica entre un protón situado en la Tierra y un electrón situado en la Luna, tiene esta misma proporción respecto a la fuerza gravitatoria entre ellas. Podemos preguntarnos entonces, ¿por qué apreciamos entonces la fuerza gravitatoria? Es más ¿por qué los planetas y galaxias se mueven por fuerzas gravitatorias y no eléctricas?

La explicación está en el hecho de que hay dos signos de carga, pero solo una de masa. Esto quiere decir que el efecto de la gravedad es siempre acumulativo, cuanta más masa se reúne, mayor es la fuerza gravitatoria. Las cargas, en cambio, se cancelan mutuamente. La materia es esencialmente neutra, ya que hay tantas cargas positivas como negativas, por lo que la fuerza eléctrica sobre un objeto distante es prácticamente nula.

Para justificar esto, no obstante, debemos considerar el efecto de un conjunto de cargas.

6 Principio de superposición

Cuando tenemos más de una carga puntual, la ley de Gauss no es suficiente para determinar el campo eléctrico, ya que no se cumple que el campo sea radial o que dependa solo de la distancia a la carga, al haber más de una. Necesitamos una ley adicional.

Esta ley adicional es el principio de superposición de los campos, que establece que

El campo de un conjunto de cargas es igual a la suma vectorial de los campos individuales, calculados como si las demás cargas no estuvieran presentes.

es decir, que podemos emplear las expresiones anteriores para los campos de cada una de las cargas y sumarlas vectorialmente en cada punto. La coletilla “como si las demás cargas no estuvieran presentes”, se refiere a que en principio, si tenemos una carga ya situada, e introducimos una adicional, la segunda podría influir en el campo de la primera, pero no lo hace.

Así, si tenemos dos cargas iguales positivas, el campo en cada punto es la suma de dos campos radiales hacia afuera respecto de cada carga. El resultado es un campo hacia el exterior del sistema, pero ya no radial. En particular, en el punto medio entre las dos cargas, los dos campos se cancelan y el campo total es nulo.

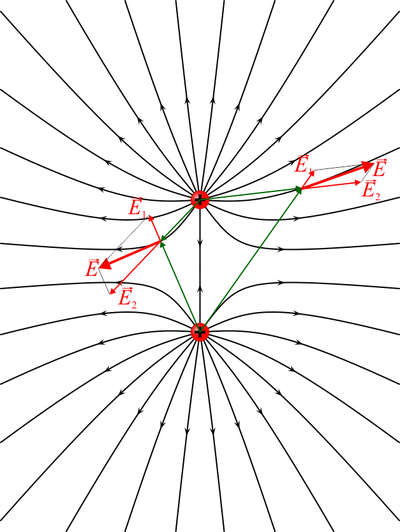
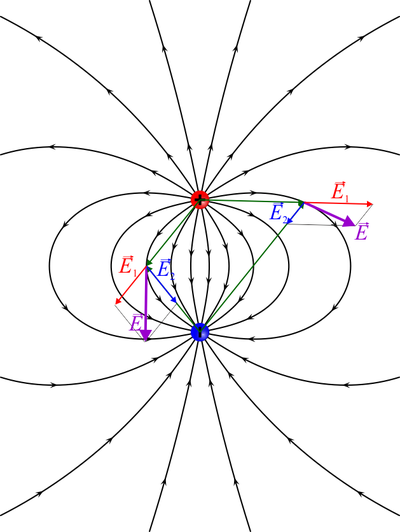
Si tenemos dos cargas iguales y opuestas, lo que se conoce como un dipolo, el campo en cada punto es suma vectorial de uno que se aleja de la carga positiva y uno que se acerca a la negativa. Las líneas de campo, en este caso, son curvas que nacen en la carga positiva y mueren en la negativa.

Matemáticamente, la suma del campo de las dos cargas sería, para cada punto

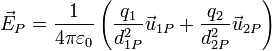
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{d_{1P}^2}\vec{u}_{1P}+\frac{q_2}{d_{2P}^2}\vec{u}_{2P}\right)$

o empleando las posiciones de las dos cargas y del punto donde deseamos hallar el campo

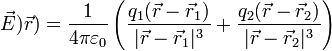
$\vec{E})\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1(\vec{r}-\vec{r}_1)}{|\vec{r}-\vec{r}_1|^3}+\frac{q_2(\vec{r}-\vec{r}_2)}{|\vec{r}-\vec{r}_2|^3}\right)$

El principio de superposición es válido también para las fuerzas eléctricas. La fuerza sobre una tercera carga puesta en el sistema será la resultante de las fuerzas producidas cpor cada una de las cargas, como si la otra no estuviera presente.

7 Campo de una distribución de carga

7.1 De cargas puntuales

El principio de superposición se extiende a cualquier número de cargas. Si tenemos N cargas puntuales, situadas en los puntos 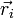$\vec{r}_i$ , el campo en cualquier punto vale

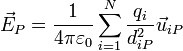
$\vec{E}_P=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i}{d_{iP}^2}\vec{u}_{iP}$

o, usando las posiciones de cada una

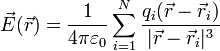
$\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i(\vec{r}-\vec{r}_i)}{|\vec{r}-\vec{r}_i|^3}$

7.2 De una distribución continua

Al considerar un medio material, se hace imposible conocer la posición de cada una de los trillones de cargas que lo componen.

Por ello, se debe trabajar con densidades de carga. Dividimos el volumen del material en elementos microscópicos (pero que contienen millones de cargas), de forma que la carga de cada elemento es $d q$ . Entonces, el campo en un punto P es la generalización de la suma anterior a una integral

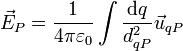
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int \frac{\mathrm{d}q}{d_{qP}^2}\vec{u}_{qP}$

siendo $d q P$ la distancia desde cada elemento de carga al punto donde queremos hallar el campo y 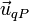$\vec{u}_{qP}$ el unitario en la dirección desde el elemento de carga al punto en cuestión.

Dependiendo del tipo de carga que tengamos, el tipo de integral variará.

Volumétrica: Si la carga está repartida en un volumen

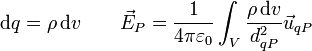
$\mathrm{d}q=\rho\,\mathrm{d}v\qquad \vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int_V \frac{\rho\,\mathrm{d}v}{d_{qP}^2}\vec{u}_{qP}$

donde

ρ

será en general una función de la posición, que habrá que integrar.

Superficial: Si la carga está distribuida sobre una superficie

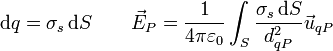
$\mathrm{d}q=\sigma_s\,\mathrm{d}S\qquad \vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int_S \frac{\sigma_s\,\mathrm{d}S}{d_{qP}^2}\vec{u}_{qP}$

Obsérvese que, a diferencia del flujo, aquí el diferencial de superficie es escalar, e igual al área del elemento.

Lineal: Si la carga está repartida a lo largo de una línea

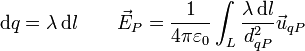
$\mathrm{d}q=\lambda\,\mathrm{d}l\qquad \vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int_L \frac{\lambda\,\mathrm{d}l}{d_{qP}^2}\vec{u}_{qP}$

Caso general: En un problema general podemos tener todos los tipos de densidades simultáneamente y además cargas puntuales aisladas. El campo en cada punto será la superposición de los campos individuales

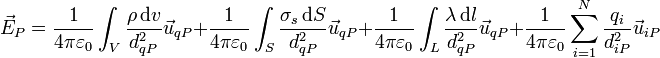
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int_V \frac{\rho\,\mathrm{d}v}{d_{qP}^2}\vec{u}_{qP}+\frac{1}{4\pi\varepsilon_0}\int_S \frac{\sigma_s\,\mathrm{d}S}{d_{qP}^2}\vec{u}_{qP}+\frac{1}{4\pi\varepsilon_0}\int_L \frac{\lambda\,\mathrm{d}l}{d_{qP}^2}\vec{u}_{qP}+\frac{1}{4\pi\varepsilon_0}\sum_{i=1}^N \frac{q_i}{d_{iP}^2}\vec{u}_{iP}$

En casi todos los casos estas integrales son imposibles de hallar analíticamente. Sin embargo, se prestan a un cálculo numérico sencillo de implementar en un ordenador: se divide la distribución en un número grande de elementos, se calcula la contribución de cada uno al campo y se halla la suma de todos ellos, como si fuera un conjunto de cargas puntuales. Existen diferentes mejoras a este método, que aumentan la precisión o la velocidad del cálculo.

7.3 Densidades uniformes

En muchos problemas prácticos se dice “una carga Q distribuida uniformemente en el volumen” o “un anillo cargado uniformemente con carga Q” o similar. En estos casos se nos está dando el tipo de distribución (si es de volumen, lineal, etc.), el valor de la carga total, y se nos dice que la carga tiene una densidad uniforme, es decir, que es la misma para todos los puntos. En esos casos, lo primero es determinar la densidad correspondiente, y luego recurrir a las expresiones anteriores.

Por ejemplo, si se nos pide hallar el campo en los puntos del eje de un anillo de radio $R$ con una carga $Q$ distribuida uniformemente, tenemos que el anillo tiene una densidad lineal de carga $λ$ , tal que

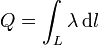
$Q = \int_L \lambda\,\mathrm{d}l$

Ahora bien, por ser la densidad uniforme, puede salir de la integral

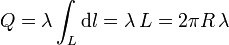
$Q = \lambda\int_L\mathrm{d}l = \lambda\,L = 2\pi R\,\lambda$

lo que nos da la densidad

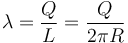
$\lambda = \frac{Q}{L}=\frac{Q}{2\pi R}$

y, para la expresión del campo nos queda

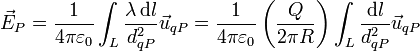
$\vec{E}_P = \frac{1}{4\pi\varepsilon_0}\int_L \frac{\lambda\,\mathrm{d}l}{d_{qP}^2}\vec{u}_{qP}=\frac{1}{4\pi\varepsilon_0}\left(\frac{Q}{2\pi R}\right)\int_L \frac{\mathrm{d}l}{d_{qP}^2}\vec{u}_{qP}$

Análogamente si tenemos el caso de una carga distribuida uniformemente en una superficie esférica

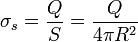
$\sigma_s = \frac{Q}{S}=\frac{Q}{4\pi R^2}$

o en un volumen esférico

$\rho = \frac{Q}{V}=\frac{3Q}{4\pi R^3}$

Campo eléctrico y ley de Gauss (GIE)

De Laplace

Contenido

1 Concepto de electrostática

2 Campo eléctrico

3 Líneas de campo eléctrico

4 Ley de Gauss

5 Campo de cargas puntuales

5.1 Ley de Coulomb

6 Principio de superposición

7 Campo de una distribución de carga

7.1 De cargas puntuales

7.2 De una distribución continua

7.3 Densidades uniformes

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES