Campo eléctrico FII GIA

De Laplace

Contenido

1 Carga eléctrica
2 Conductores y aislantes
- 2.1 Carga por inducción
3 Ley de Coulomb
- 3.1 Principio de superposición
4 Campo eléctrico
5 Líneas de campo
- 5.1 Ejemplos de configuraciones de líneas de campo
6 Ley de Gauss
- 6.1 Flujo eléctrico
- 6.2 Cálculo del campo eléctrico usando la ley de Gauss
7 Fuerza y par sobre un dipolo
8 Discontinuidad de la componente normal del campo
9 Equilibrio electrostático en un conductor

1 Carga eléctrica

Las primeras observaciones de fenómenos eléctricos de las que tenemos noticias fueron hechas por los griegos. Se dieron cuenta de que después de frotar un trozo de ámbar con piel curtida, el ámbar era capaz de atraer objetos pequeños y ligeros, como pajitas o plumas. Podemos realizar fácilmente una experiencia similar frotando un bolígrafo de plástico con un chaleco de lana. Veremos que el bolígrafo es capaz de atraer pequeños trozos de papel. Como curiosidad, el término electricidad deriva de la palabra griega para ámbar: elektron.

1.1 Tipos de carga eléctrica

En la experiencia se observa que:

Dos barras de caucho frotadas con piel se repelen.
Dos barras de vidrio frotadas con seda se repelen.
Una barra de caucho frotada con piel y una barra de vidrio frotada con seda se atraen.

Estos hechos experimentales se pueden explicar postulando la existencia de dos tipos de carga. Objetos con el mismo tipo de carga se repelen y objetos con distinto tipo de carga se atraen.

Siguiendo la nomenclatura impuesta por Benjamin Franklin, un tipo de carga se llama positivo y el otro negativo. Cuál es cual es una cuestión de convenio. En nuestro experimento la barra de caucho tiene carga negativa y la de vidrio positiva. En principio podría haber tantos tipos de carga como materiales, pero puede comprobarse que es suficiente con considerar dos tipos de carga (¿cómo puede comprobarse esto?)

Con esta hipótesis, los hechos experimentales se explican de la siguiente manera. Al frotar la barra de caucho con la piel, cargas negativas de la piel pasan al caucho, con lo que este queda con carga neta negativa y la piel con carga neta positiva. Hoy sabemos que en el frotamiento se transfieren electrones desde la piel al caucho. En el caso del vidrio y la seda los signos son los contrarios, pues los electrones se transfieren desde el vidrio hacia la seda.

Este fenómeno de carga por frotamiento se llama triboelectricidad, del griego tribos (rozamiento, frotamiento).

1.2 Cuantización de la carga eléctrica

La unidad de carga eléctrica observada en la Naturaleza en estado libre es la carga del electrón (o protón). Los átomos tienen un núcleo cargado positivamente y electrones a su alrededor con carga negativa. El núcleo está compuesto de protones, con carga positiva, y neutrones, que tienen carga neta nula. El valor absoluto de la carga eléctrica de un protón y un electrón es el mismo

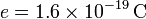
$e=1.6\times10^{-19}\,\mathrm{C}$

Siendo el Coulombio (C) la unidad de carga eléctrica en el sistema internacional.

Cuando un cuerpo está cargado, su carga total es siempre un múltiplo entero de esta carga fundamental

$|Q| = N\,e$

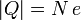
En general, el número $N$ es enorme. Por dar una idea, cuando se frota caucho con piel su valor es 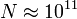$N \approx10^{11}$ .

1.3 Conservación de la carga

La carga eléctrica neta se conserva en cualquier proceso de la Naturaleza. En los experimentos triboeléctricos anteriores, al frotar el caucho con la piel la cantidad de carga negativa que adquiere el caucho es igual en valor absoluto a la cantidad de carga positiva que adquiere la piel.

Esto no quiere decir que no pueda crearse carga. Lo que impone es que la carga neta se mantiene constante. Así un fotón puede descomponerse en un electrón y un positrón (antipartícula del electrón con carga positiva). En este proceso se crean dos cargas eléctricas nuevas, pero la carga neta no varía (es nula antes y después del proceso)

2 Conductores y aislantes

Desde el punto de vista del movimiento de las cargas en su interior, los materiales pueden clasificarse en conductores y aislantes.

En los materiales aislantes la carga eléctrica no puede desplazarse por él. Si frotamos el extremos de un bolígrafo de plástico con lana, el extremo frotado es capaz de atraer trocitos de papel, pero el extremo no frotado no puede hacerlo. Esto se debe a que el plástico es aislante, y la carga queda confinada al extremo en el que se depositó. Ejemplos de materiales aislantes son los plásticos, la cera, papel, madera, etc.

En los materiales conductores, las cargas que se depositan en ellos pueden moverse libremente por el volumen del material. Ejemplos de esto son los metales, disoluciones salinas, plasmas (gas disociado en iones, como en los tubos fluorescentes), etc.

Es interesante definir el concepto de conductor perfecto como un material conductor en el que existe de forma natural un número infinito de cargas libres. Un buen ejemplo son los metales. En un centímetro de cobre hay del orden de $1023$ electrones libres con capacidad para moverse por su volumen.

2.1 Carga por inducción

Este es un fenómeno por el cual se puede obtener una carga neta en un conductor sin necesidad de tocarlo.

Tenemos una barra de vidrio cargada positivamente por rozamiento. Si acercamos esta barra a una esfera conductora (por ejemplo, metálica) las cargas negativas de la esfera se acercan a la barra, dejando el lado opuesto con una carga positiva.

Si ahora colocamos otra esfera metálica en contacto con la primera en el punto más alejado de la barra, las cargas negativas de la segunda esfera se acercan a la barra cargada, con lo que el extremo de la segunda esfera más alejado de la barra tiene carga neta positiva.

Si ahora separamos las dos esferas y alejamos la barra cargada, la primera queda con una carga neta negativa y la segunda con una carga neta positiva.

3 Ley de Coulomb

Dadas dos cargas eléctricas puntuales $q 1$ y $q 2$ , se observa experimentalmente que la fuerza entre ellas tiene las siguientes propiedades

Su módulo es proporcional al módulo del producto de las cargas.
Su módulo es inversamente proporcional al cuadrado de la distancia entre ellas.
Es repulsiva si son del mismo tipo atractiva si son de distinto tipo.
Su dirección coincide con la recta que une las dos cargas.
Cumple el principio de acción y reacción.

Todas estas características se expresan matemáticamente en la Ley de Coulomb

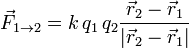
$\vec{F}_{1\to2} = k\,q_1\,q_2\dfrac{\vec{r}_2-\vec{r}_1}{|\vec{r}_2-\vec{r}_1|}$

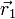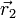Los vectores $\vec{r}_1$ y $\vec{r}_2$ indican las posiciones de las partículas respectivas. La constante $k$ es la constante de Coulomb. No tiene significado físico y únicamente establece el valor de las unidades. En el SI vale

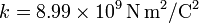
$k = 8.99\times10^9\,\mathrm{N\,m^2/C^2}$

Otra forma de escribir esta constante es

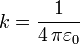
$k=\dfrac{1}{4\,\pi\varepsilon_0}$

donde $\varepsilon_0$ es la permitividad del vacío y vale, en el SI

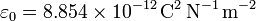
$\varepsilon_0 = 8.854\times10^{-12}\,\mathrm{C^2\,N^{-1}\,m^{-2}}$

Validez de la ley de Coulomb: esta ley es válida cuando

Las cargas son puntuales. Esto ocurre si la longitud típica de las cargas es muy pequeña comparada con la distancia que las separa (si fueran esferas esa longitud típica es su radio)
Las dos cargas estén en reposo. Si una de ellas está moviéndose se puede usar para calcular la fuerza que la carga en reposo ejerce sobre la que se mueve (como en el átomo de hidrógeno)

3.1 Principio de superposición

Si tenemos un conjunto de cargas 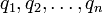$q_1, q_2,\ldots,q_n$ situadas en los puntos 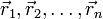$\vec{r}_1,\vec{r}_2,\ldots,\vec{r}_n$ , la fuerza total que sufre una carga $q$ debido a todas ellas es la suma vectorial de la fuerza ejercida por cada carga. Es decir

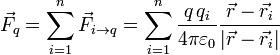
$\vec{F}_q = \sum\limits_{i=1}^n\vec{F}_{i\to q} = \sum\limits_{i=1}^n\dfrac{q\,q_i}{4\pi\varepsilon_0} \dfrac{\vec{r}-\vec{r}_i}{|\vec{r}-\vec{r}_i|}$

donde $\vec{r}$ indica la posición de la carga $q$ .

4 Campo eléctrico

Un conjunto de cargas puntuales 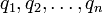$q_1, q_2, \ldots, q_n$ ejerce una fuerza sobre una carga puntual $q 0$ dada por la ley de Coulomb. Esta es la visión de acción a distancia.

En la visión de campo eléctrico, el sistema de cargas puntuales crea un campo vectorial en el espacio, y es el campo el que ejerce la fuerza sobre la carga. El campo eléctrico creado en cada punto por el sistema de cargas es

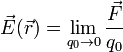
$\vec{E}(\vec{r}) = \lim\limits_{q_0\to0}\dfrac{\vec{F}}{q_0}$

La carga $q 0$ se hace tender a cero para que no cree ella misma un campo eléctrico lo bastante intenso como para que afecte al sistema de cargas puntuales. Se le llama a veces carga testigo.

El campo eléctrico es un vector, es decir, en cada punto su dirección puede cambiar. Podríamos medirlo experimentalmente colocando la carga testigo en diferentes puntos, midiendo en cada uno la fuerza sobre ella con un dinamómetro y dividiendo esta fuerza por el valor de la carga testigo.

La unidad en el SI es N/C.

4.1 Campo eléctrico de una carga puntual

Consideramos una carga puntual $q$ en el origen del sistema de ejes. La fuerza que ejerce sobre una carga testigo es

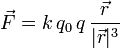
$\vec{F} = k\,q_0\,q\,\dfrac{\vec{r}}{|\vec{r}|^3}$

En esta expresión el vector $\vec{r}$ indica la posición de la carga testigo.

A partir de la definición de campo eléctrico, el campo de una carga puntual es

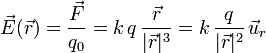
$\vec{E}(\vec{r}) = \dfrac{\vec{F}}{q_0} = k\,q\,\dfrac{\vec{r}}{|\vec{r}|^3} = k\,\dfrac{q}{|\vec{r}|^2}\,\vec{u}_{r}$

Aquí, $\vec{r}$ es el vector de posición de cada punto del espacio, con lo que $|\vec{r}|$ es la distancia de cada punto del espacio a la carga. El vector 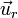$\vec{u}_r$ es un vector unitario en la dirección de $\vec{r}$ .

En cada punto, el módulo del campo es proporcional a la carga e inversamente proporcional al cuadrado de la distancia. Su dirección es radial, alejándose de la carga si esta es positiva y hacia ella si es negativa.

Si la carga no está en el origen, sino en un punto con vector de posición 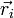$\vec{r}_{i}$ el campo creado por la carga en un punto del espacio dado por 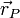$\vec{r}_P$ es

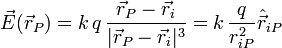
$\vec{E}(\vec{r}_P) = k\,q\,\dfrac{\vec{r}_P-\vec{r}_i}{|\vec{r}_P-\vec{r}_i|^3} = k\,\dfrac{q}{r_{iP}^2}\hat{\vec{r}}_{iP}$

En esta expresión, el vector 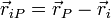$\vec{r}_{iP}=\vec{r}_P-\vec{r}_i$ es el vector que va desde el punto donde está la carga hasta el punto en el que queremos calcular el campo. El vector

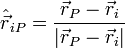
$\hat{\vec{r}}_{iP} = \dfrac{\vec{r}_P-\vec{r}_i}{|\vec{r}_P-\vec{r}_i|}$

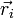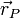es un vector unitario que va desde $\vec{r}_i$ hasta $\vec{r}_{P}$ .

4.2 Campo eléctrico de una distribución de cargas puntuales

Dado un conjunto de cargas puntuales 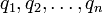$q_1, q_2, \ldots, q_n$ , cada una de ellas con un vector de posición 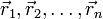$\vec{r}_1, \vec{r}_2, \ldots, \vec{r}_n$ , el campo creado por este conjunto de cargas en un punto $P$ con vector de posición 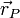$\vec{r}_P$ es

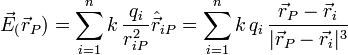
$\vec{E}_(\vec{r}_P) = \sum\limits_{i=1}^n k\,\dfrac{q_i}{r_{iP}^2}\hat{\vec{r}}_{iP} = \sum\limits_{i=1}^n k\,q_i\, \dfrac{\vec{r}_P-\vec{r}_i}{|\vec{r}_P-\vec{r}_i|^3}$

Si una carga $q$ se coloca en el punto $P$ la fuerza que sobre ella ejerce el conjunto de cargas puntuales se calcula como

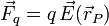
$\vec{F}_q = q\,\vec{E}(\vec{r}_P)$

4.3 Campo eléctrico de una distribución continua de carga

Hemos visto que la carga está cuantizada. Esto quiere decir que si un cuerpo tiene una carga $Q$ , esta carga es un múltiplo entero de la carga fundamental, 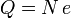$Q=N\,e$ . En las situaciones habituales, el número $N$ es tan grande que la distribución de carga puede tratarse como un continuo.

Consideremos un cuerpo de volumen $τ$ con una cierta distribución de carga. Esta distribución viene descrita por una densidad volumétrica de carga 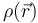$\rho(\vec{r})$ . Consideramos un pequeño volumen $Δ V$ en un punto del cuerpo. La carga presente en ese elemento de volumen es $Δ q$ . El valor de la densidad volumétrica de carga en ese punto es

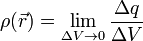
$\rho(\vec{r}) = \lim\limits_{\Delta V\to 0}\dfrac{\Delta q}{\Delta V}$

El límite en esta expresión hay que entenderlo como un límite físico. Si $Δ V$ tendiese estrictamente a cero, al final nos quedaríamos sin cargas, pues la distribución de la materia es discontinua a escala atómica. Desde el punto de vista físico el límite hay que entenderlo como un volumen pequeño comparado con el tamaño del cuerpo y lo bastante grande como para que haya muchas cargas dentro de él. A título de ejemplo, en un 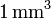$1\,\mathrm{mm^3}$ de cobre hay del orden de $1021$ electrones.

Cuando se nos proporciona el valor de la densidad de carga en cada punto de un cuerpo, podemos calcular la carga de un pequeño elemento de volumen $d V$ . Esta carga será

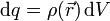
$\mathrm{d}q = \rho(\vec{r})\,\mathrm{d}V$

De este modo un cuerpo con una distribución continua de carga puede considerarse formado por un número infinito de pequeñas cargas puntuales, cada una de ellas un pequeño volumen con una carga

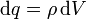
$\mathrm{d}q = \rho\,\mathrm{d}V$

El campo en un punto 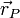$\vec{r}_P$ del espacio es la suma del campo creado por cada uno de los elementos de carga en que dividimos el cuerpo

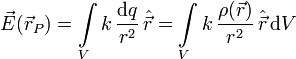
$\vec{E}(\vec{r}_P) = \int\limits_V k\,\dfrac{\mathrm{d}q}{r^2}\,\hat{\vec{r}} = \int\limits_V k\,\dfrac{\rho(\vec{r})}{r^2}\,\hat{\vec{r}}\,\mathrm{d}V$

Para cada elemento de volumen, el vector 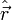$\hat{\vec{r}}$ es un vector de módulo unidad que apunta desde la posición del elemento de volumen hacia el punto $P$ donde queremos calcular el campo.

En general la densidad de carga puede variar de un punto a otro del cuerpo cargado.

4.3.1 Cuerpo cargado en superficie

En muchas ocasiones la carga eléctrica se distribuye en una capa de grosor muy fino. Esto ocurre en los conductores cargados en equilibrio electrostático. En ese caso la distribución de carga puede considerarse superficial (por ejemplo, un plano cargado o la superficie de una esfera). La magnitud que describe la distribución de carga eléctrica es la densidad superficial de carga, $σ$ . Ahora consideramos la distribución de carga compuesta de elementos de área, $d A$ , cada uno con una carga

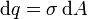
$\mathrm{d}q = \sigma\,\mathrm{d}A$

El campo creado en un punto 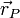$\vec{r}_P$ por una distribución superficial de carga se obtiene aplicando de nuevo el Principio de Superposición. Cada elemento de superficie es una carga puntual, y el campo total es

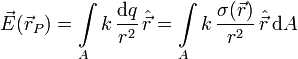
$\vec{E}(\vec{r}_P) = \int\limits_A k\,\dfrac{\mathrm{d}q}{r^2}\,\hat{\vec{r}} = \int\limits_A k\,\dfrac{\sigma(\vec{r})}{r^2}\,\hat{\vec{r}}\,\mathrm{d}A$

Para cada elemento de área, el vector 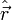$\hat{\vec{r}}$ es un vector de módulo unidad que apunta desde la posición del elemento de área hacia el punto $P$ donde queremos calcular el campo.

En general la densidad superficial de carga puede variar de un punto a otro de la superficie cargada.

4.3.2 Línea cargada

Cuando tenemos un hilo delgado, la posición a lo largo del hilo puede indicarse con una sola coordenada (por ejemplo, la longitud recorrida sobre el hilo). Si el hilo tiene carga, podemos dividirlo en elementos de línea de longitud $d l$ . Cada elemento de línea es una carga puntual con carga

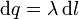
$\mathrm{d}q = \lambda\,\mathrm{d}l$

La magnitud $λ$ es la densidad lineal de carga eléctrica.

Si queremos calcular el campo producido por una distribución de este tipo en punto del espacio $P$ , utilizamos de nuevo el Principio de Superposición para calcular el campo como la suma de los campos creados por cada elemento de línea. Así

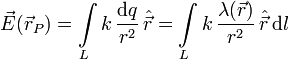
$\vec{E}(\vec{r}_P) = \int\limits_L k\,\dfrac{\mathrm{d}q}{r^2}\,\hat{\vec{r}} = \int\limits_L k\,\dfrac{\lambda(\vec{r})}{r^2}\,\hat{\vec{r}}\,\mathrm{d}l$

Para cada elemento de línea, el vector 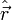$\hat{\vec{r}}$ es un vector de módulo unidad que apunta desde la posición del elemento de línea hacia el punto $P$ donde queremos calcular el campo.

En general la densidad lineal de carga puede variar de un punto a otro de la línea cargada.

5 Líneas de campo

Las líneas de campo o líneas de fuerza son una forma de visualizar el campo eléctrico de un conjunto de cargas. Son líneas que en cada punto son tangentes al vector campo eléctrico.

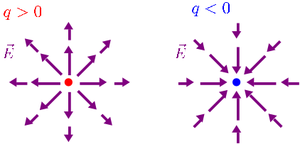
En el caso de una carga puntual, en cada punto el campo eléctrico es radial respecto de la carga. Por tanto la líneas de campo son líneas radiales que parten de la carga, si esta es positiva, y entran en ella si es negativa.

A la hora de representar las líneas de campo de una carga, el número de líneas que salen o entran en ella es proporcional al valor de su carga. Si tenemos dos cargas $q 2$ y $q 1$ , con $| q 2 | = 2 | q 1 |$ , el número de líneas que salen de $q 2$ será el doble que el número de lineas que salen de $q 1$ .

La intensidad del campo eléctrico en una región es proporcional a la densidad de líneas de campo. En un carga puntual, las líneas están más cerca cerca de la carga, donde el campo es más intenso, y se separan conforme nos alejamos de la carga.

En un sistema con carga neta no nula, debe haber líneas que lleguen hasta el infinito (hacia el infinito si la carga neta es positiva y viniendo del infinito si es negativa). Esto refleja el hecho de que si miramos el sistema desde muy lejos no vemos el detalle de la situación de las cargas puntuales. Sólo vemos su carga neta, y el campo debe ser similar al de una carga puntual de valor igual a la carga neta del sistema.

Las líneas de campo no representan las trayectorias de un carga en el campo eléctrico.

Dos líneas de campo no pueden cruzarse. Si ocurriera esto, en el punto en que se cruzan el campo tendría dos valores distintos. Y esto no puede ocurrir, el campo eléctrico es una función univaluada en cada punto del espacio.

5.1 Ejemplos de configuraciones de líneas de campo

6 Ley de Gauss

La ley de Gauss es una de las cuatro leyes de Maxwell, y como tal una de las leyes básicas del Electromagnetismo. Relaciona el flujo de campo eléctrico a través de una superficie cerrada con la carga neta encerrada en esa superficie. Está basada en las propiedades de simetría espacial del campo eléctrico.

6.1 Flujo eléctrico

6.1.1 Campo uniforme y superficie perpendicular

Consideremos una región del espacio donde hay definido un campo eléctrico uniforme. Si dibujamos una superficie que sea perpendicular al campo eléctrico, podemos imaginar las líneas de campo eléctrico atravesando esta superficie. Este es el flujo del campo eléctrico. Es similar al flujo de agua a través de la sección de una tubería. Definimos el flujo eléctrico a través de una superficie perpendicular al campo como

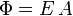
$\Phi = E\,A$

siendo $A$ el área de la superficie. El flujo es proporcional al número de líneas de campo eléctrico que atraviesan la superficie.

6.1.2 Campo uniforme y superficie inclinada

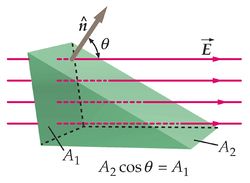
Consideramos ahora el caso en el que la superficie no es normal al campo eléctrico. La imagen de la derecha muestra dos superficies $A 1$ y $A 2$ . La primera de ellas es perpendicular al campo, mientras que la segunda está inclinada. Esta inclinación puede medirse como el ángulo $θ$ que forma el vector normal a la superficie, 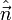$\hat{\vec{n}}$ con el campo.

Podemos observar que el número de líneas de campo que atraviesan las dos superficies es el mismo. Entonces el flujo a través de la superficie $A 2$ es

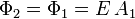
$\Phi_2 = \Phi_1 = E\,A_1$

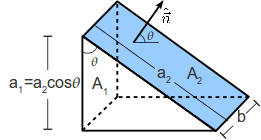
Podemos relacionar el área de las dos superficies usando la figura de la izquierda. Vemos que

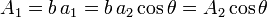
$A_1 = b\,a_1 = b\,a_2\cos\theta = A_2\cos\theta$

Por tanto, el flujo a través de la superficie inclinada es

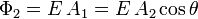
$\Phi_2 = E\,A_1 = E\,A_2\cos\theta$

Esto se puede expresar en forma vectorial usando el vector unitario normal a la superficie. Para una superficie general, tenemos

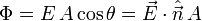
$\Phi = E\,A\cos\theta = \vec{E}\cdot\hat{\vec{n}}\,A$

6.1.3 Campo no uniforme y superficie arbitraria

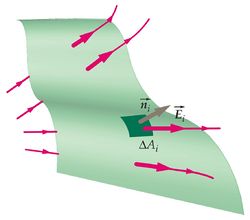
En el caso más general el campo eléctrico varía de un punto a otro de la superficie y ésta puede tener cualquier forma. Recurrimos entonces al cálculodiferencial. Dividimos la superficie en elementos de área, cada elemento con un vector normal 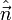$\hat{\vec{n}}$ y área $d A$ . El flujo a través de cada elemento es

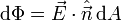
$\mathrm{d}\Phi = \vec{E}\cdot\hat{\vec{n}}\,\mathrm{d}A$

El flujo a través de toda la superficie es la suma de los flujos a través de cada elemento de área que podemos tomar en ella. Es decir

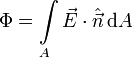
$\Phi = \int\limits_A \vec{E}\cdot\hat{\vec{n}}\,\mathrm{d}A$

6.1.4 Superficie cerrada

Una superficie cerrada divide al espacio en dos partes, el interior y el exterior. Por convenio, el vector normal a una superficie cerrada se considera positivo cuando apunta hacia el exterior de la superficie. Al calcular el flujo del campo a través de una superficie cerrada se coloca un pequeño círculo en el signo integral

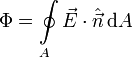
$\Phi = \oint\limits_A \vec{E}\cdot\hat{\vec{n}}\,\mathrm{d}A$

6.2 Cálculo del campo eléctrico usando la ley de Gauss

7 Fuerza y par sobre un dipolo

7.1 Definición de dipolo eléctrico

Un dipolo está compuesto por dos cargas puntuales de igual magnitud y signo contrario separadas por una distancia $d$ . Se caracteriza por el vector momento dipolar

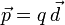
$\vec{p} = q\,\vec{d}$

Aquí, $q$ es el valor absoluto de las cargas del dipolo y el vector 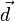$\vec{d}$ se dirige desde la carga negativa hacia la positiva y su módulo es la distancia que las separa.

7.2 Par sobre un dipolo

Cuando un dipolo es sometido a la acción de un campo eléctrico, éste tiende a girarlo, de modo que se orienta en la dirección del campo. El momento de la fuerza eléctrica respecto del centro del dipolo es

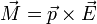
$\vec{M} = \vec{p}\times\vec{E}$

7.3 Fuerza sobre un dipolo

La fuerza neta sobre un dipolo en el seno de un campo eléctrico uniforme es nula, pues la fuerza es la misma en módulo sobre las dos cargas del dipolo y con sentidos opuestos

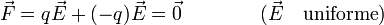
$\vec{F} = q\vec{E} + (-q)\vec{E} = \vec{0} \qquad\qquad(\vec{E}\quad\mathrm{uniforme})$

Si el campo es no uniforme, una vez que el dipolo está orientado en la dirección y sentido del campo, éste ejerce una fuerza sobre él que lo empuja hacia la zona de campo intenso. Consideremos una carga puntual positiva y un dipolo cerca de ella orientado en la dirección y sentido del campo que crea la carga puntual. La carga negativa del dipolo está más cerca de la carga puntual que la positiva, por lo que la intensidad de la fuerza es mayor sobre la carga negativa, atrayendo al dipolo hacia la carga puntual.