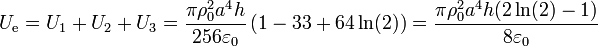Campo de una distribución cilíndrica
De Laplace
Contenido |
1 Enunciado
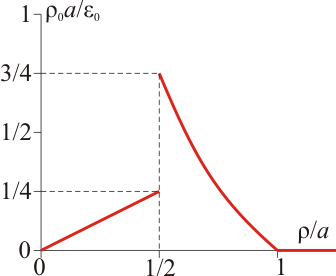
Un cilindro de radio a y longitud indefinida, mucho mayor que el radio, está relleno de sendas distribuciones de carga eléctrica de signo opuesto y densidades volumétricas constantes ρ0 y − ρ0, según se muestra en la figura. Además, en la superficie de separación entre ambas distribuciones, ρ = a / 2, existe una distribución superficial uniforme de carga.- Calcule el valor de dicha densidad superficial de carga si el campo eléctrico es nulo en los puntos exteriores al cilindro
- Obtenga la expresión del campo eléctrico en todo el espacio
- Calcule la diferencia de potencial entre el centro de la distribución y la superficie exterior.
- Halle la densidad de energía electrostática en cualquier punto del espacio, así como la energía almacenada entre dos planos z = 0 y z = h.
2 Solución
2.1 Densidad superficial de carga
Si el campo exterior es nulo, al calcular su flujo a través de una superficie cilíndrica de radio ρ y altura h, exterior al cilindro de carga el flujo es nulo. Esto quiere decir, por aplicación de la ley de Gauss, que también lo es la carga encerrada en este cilindro
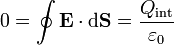
A su vez la carga encerrada es la suma de la carga de volumen y de la superficial
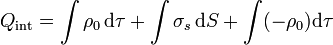
Como las tres distribuciones son uniformes, la contribución de cada una es igual al integrando multiplicado por el dominio de integración (un cilindro, una superficie cilíndrica y una corona cilíndrica), esto es
- Cilindro interior
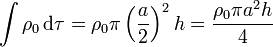
- Superficie cilíndrica intermedia
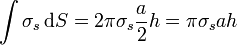
- Corona cilíndrica exterior
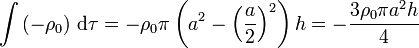
Sumando las tres contribuciones e imponiendo la anulación
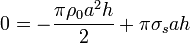

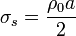
2.2 Campo eléctrico
Una vez que tenemos las densidades de carga podemos hallar el campo eléctrico aplicando la ley de Gauss en forma integral.
Por la simetría del sistema podemos considerar que el potencial eléctrico depende exclusivamente de la distancia al eje del cilindro y por tanto el campo eléctrico es radial y dependiente de esta misma distancia


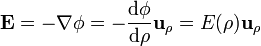
Si consideramos una superficie cilíndrica de altura h y radio ρ < a, el flujo del campo eléctrico a través de esta superficie contiene solamente la contribución de la cara lateral, en la cual el módulo del campo es constante

Este flujo debe ser igual a la carga encerrada dividida por  . Tenemos tres posibilidades
. Tenemos tres posibilidades
2.2.1 En el cilindro interior
Si consideramos ρ < a / 2, la carga encerrada es la contenida en un volumen cilíndrico de radio ρ con densidad uniforme ρ0
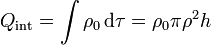
Aplicando la ley de Gauss
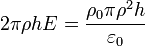

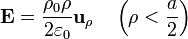
2.2.2 En la corona cilíndrica
Si consideramos a / 2 < ρ < a, tenemos tres contribuciones a la carga encerrada:
- la de un cilindro de radio a / 2, con densidad + ρ0
- la de la superficie cilíndrica de radio a / 2, con densidad σs = ρ0a / 2
- la contenida en una corona cilíndrica de radio interior a / 2 y exterior ρ, con densidad − ρ0

Aplicando la ley de Gauss
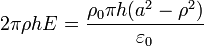

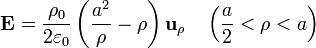
2.2.3 En el exterior del sistema
Si el radio de la superficie de integración ρ > a, la carga encerrada es nula, tal como vimos en el primer aparatdo, por tanto
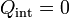
y también lo es el campo eléctrico
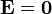
2.2.4 Expresión completa
Reuniendo los tres resultados
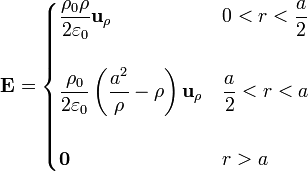
- Es nulo en el origen, como se puede deducir por simetría (las contribuciones de cargas situadas simétricamente se cancela mutuamente)
- Crece linealmente con la distancia para ρ < a / 2, como en el caso de un solo cilindro homogéneo.
- Tiene una discontinuidad en ρ = a / 2, como corresponde a la presencia de una densidad de carga superficial. Este salto es
![\mathbf{n}\cdot[\mathbf{E}] = \mathbf{u}_\rho\cdot\left(\mathbf{E}\left(\frac{a^+}{2}\right)-\mathbf{E}\left(\frac{a^-}{2}\right)\right) = \frac{\rho_0}{2\varepsilon_0}\,\frac{3a}{2}-\frac{\rho_0}{2\varepsilon_0}\,\frac{a}{2}=\frac{\rho_0a}{2\varepsilon_0}=\frac{\sigma_s}{\varepsilon_0}](/wiki/images/math/d/8/9/d89144bfd27616c23c9142dcb1556096.png)
- Se anula en ρ = a. En este punto el campo es continuo, pues en la superficie exterior del cilindro no hay ninguna distribución de carga superficial.
- Es nulo para todo ρ > a, como corresponde a que la carga total sea nula y además su distribución sea simétrica. El campo de las cargas positivas se cancela con el de las negativas.
2.2.5 Aplicando el principio de superposición
El campo eléctrico puede también calcularse considerando la distribución como una superposición de distribuciones más elementales cuyo campo es conocido.
El campo creado por una superficie cilíndrica de longitud infinita y radio b cargada uniformemente con densidad superficial σs es
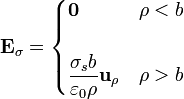
esto es, análogamente al caso de una superficie esférica, el campo en el interior es nulo y el exterior equivale al de una carga situada en el centro del cilindro (una línea de carga en este caso).
Igualmente, el campo eléctrico debido a un cilindro de radio b y longitud infinita, cargado con una densidad uniforme ρ0 produce un campo eléctrico
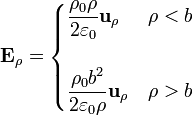
que, análogamente al caso de la esfera cargada uniformemente en volumen, es lineal con la distancia en el interior y decae en el exterior como el de una línea de carga situada en el centro del cilindro.
La distribución de carga de este problema puede describirse como la superposición de tres distribuciones de carga:
- Un cilindro de radio a y densidad de carga − ρ0, que produce un campo
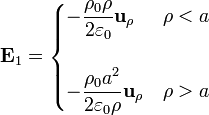
- Una densidad de carga superficial σs = ρ0a / 2 situada sobre un cilindro de radio a / 2, que produce el campo
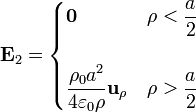
- Un cilindro de radio a / 2 y densidad de carga + 2ρ0 (el 2, para compensar el -1 que hemos introducido con el cilindro de radio a), que produce un campo

Sumando las tres contribuciones

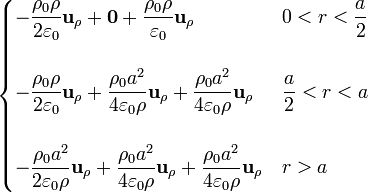
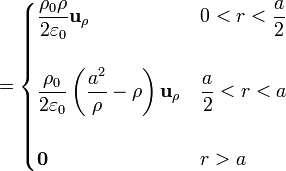
2.3 Diferencia de potencial
La diferencia de potencial la obtenemos integrando el campo eléctrico a lo largo de un camino radial que vaya desde el eje del cilindro hasta su superficie
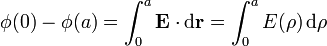
Esta integral se compone de dos tramos, uno por el cilindro interior y otro por la corona cilíndrica

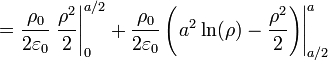
Sustituyendo los límites de integración
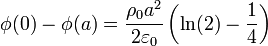
Esta diferencia de potencial es positiva, como corresponde a que el campo sea radial y hacia afuera en todos los puntos, yendo de las regiones de mayor potencial a las de menor potencial.
2.4 Densidad de energía electrostática
A partir del campo eléctrico, la densidad de energía electrostática es inmediata
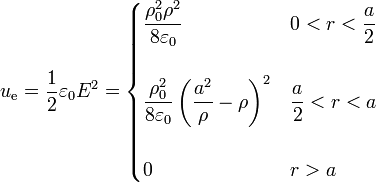
La energía total almacenada en una porción del sistema comprendida entre dos secciones planas z = 0 y z = h será la integral de volumen de esta densidad. Esta integral se compone de tres contribuciones que hay que sumar:
- En el cilindro interior (0 < ρ < a / 2)
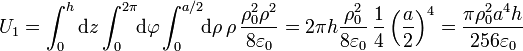
- En la corona cilíndrica (a / 2 < ρ < a)
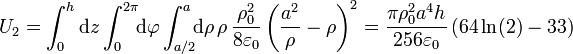
- En el exterior del cilindro (ρ > a)
La energía total contenida en esta porción del espacio es