Cálculos de carga total, campo y potencial
De Laplace
Contenido |
1 Enunciado
Calcule la carga total de las siguientes distribuciones de carga:
- N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en
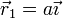 .
.
- Un anillo circular de radio R con una densidad lineal de carga uniforme λ0.
- Un anillo circular de radio R con centro el origen y situado en el plano XY, con una densidad lineal de carga
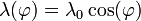 , siendo
, siendo  el ángulo del vector de posición con el eje OX.
el ángulo del vector de posición con el eje OX.
- Una superficie esférica de radio a con una densidad de carga uniforme σ0, rodeada por una superficie esférica concéntrica de radio b con densidad de carga − σ0.
- Una esfera maciza de radio R con densidad de carga uniforme ρ0.
- Una esfera maciza de radio R con una densidad de carga dependiente de la distancia al centro como
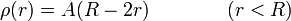
Calcule el campo y el potencial eléctrico en el origen de coordenadas para todos los sistemas del problema
2 Cargas en un polígono
2.1 Carga total
En un sistema de cargas puntuales, la carga total es la suma de todas ellas. Puesto que en este caso son todas iguales, el resultado es simplemente
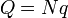
2.2 Campo eléctrico en el origen
El campo eléctrico creado por una distribución de cargas es la suma vectorial de los campos individuales
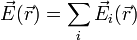
En un polígono regular todas las cargas están a la misma distancia del centro, por lo que el módulo del campo que cada una produce en el centro es el mismo para todas ellas
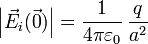
Esto no quiere decir que todas las cargas produzcan el mismo campo en el origen, ya que la dirección y el sentido de cada uno es diferente.
La dirección del campo de cada una de las cargas es en la dirección radial desde la carga hacia el punto O y su sentido será alejándose de la carga si esta es positiva y hacia ella si es negativa.
La suma de todos los campos que tienen el mismo módulo y van en la dirección radial mencionada, es nula.
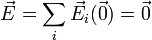
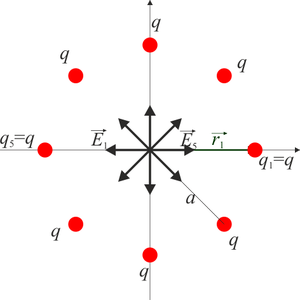
Si el número de cargas es par, el hecho es evidente. El campo de cada carga se cancela con el de la carga opuesta y el resultado es un campo nulo.
El resultado también es cierto si el número de cargas en impar. En ese caso, podemos hallar el campo resultante en el origen sumando vectorialmente los campos individuales a base de situar uno a continuación del siguiente. El resultado es otro polígono regular en el que el extremo del último vector coincide con el origen del primero, siendo la resultante nula.

2.3 Potencial eléctrico en el origen
El potencial electrostático total es una cantidad escalar que se calcula sumando los potenciales debidos a cada de las cargas

En este caso, todas las cargas tienen la misma magnitud q y están a la misma distancia a del centro, por lo que todas producen el mismo potencial en este punto y

3 Anillo cargado uniformemente
3.1 Carga total
Cuando tenemos una densidad de carga lineal, la carga total es la suma de los diferenciales de carga
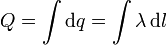
Si la densidad de carga es uniforme puede salir de la integral y queda
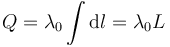
que para el caso de un anillo es
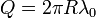
3.2 Campo en el origen
En el caso del anillo cargado uniformemente, como en el caso del polígono, el campo debido a una porción del anillo se cancela con el producido por la porción opuesta, resultando un campo total nulo.
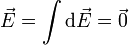
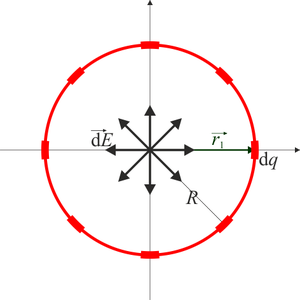
3.3 Potencial en el origen
De nuevo como en el caso del polígono (del cual el anillo es un límite), el potencial eléctrico en el centro producido por elementos de carga del mismo tamaño, por estar todos a la misma distancia R del centro

lo cual da el potencial total

En función de la densidad de carga
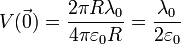
4 Anillo cargado no uniformemente
4.1 Carga total
Cuando tenemos una densidad de carga lineal, la carga total es la suma de los diferenciales de carga
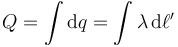
En un anillo circular, la longitud de un arco diferencial es proporcional al ángulo que abarca
![\mathrm{d}\ell' = R\,\mathrm{d}\theta'\qquad\qquad \theta\in (-\pi,\pi]](/wiki/images/math/d/8/e/d8e97e243c45da4fe95c55889f6475b5.png)
En el caso de la densidad de carga que varía como el coseno del ángulo, la carga total es

Este resultado se interpreta observando que, para una dependencia cosenoidal, la mitad del anillo posee carga positiva y la mitad negativa. Dado que el coseno es positivo en el primer y cuarto cuadrantes, y negativo en el segundo y el tercero, tenemos que toda la parte correspondiente a x > 0 posee carga positiva, que va disminuyendo hasta anularse donde corta al eje OY y para x < 0 la densidad de carga es negativa. La carga de un elemento es igual y opuesta a la del elemento simétrico. Puesto que las cargas se cancelan a pares, la carga total es nula.
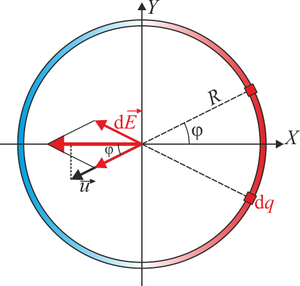
4.2 Campo en el origen
A diferencia del caso de un anillo cargado uniformemente, en una distribución de carga cosenoidal, resulta un campo no nulo. Puesto que el campo va de las cargas positivas a las negativas, el resultado va a ser un campo en la dirección del eje X, en el sentido de 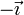 .
.
La expresión general para el campo debido a una distribución lineal de carga es
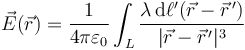
En nuestro caso
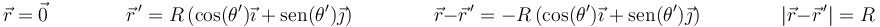
y, como se ha dicho antes

Todo esto nos da la integral

Esta integral es menos temible de lo que parece, ya que hay muchos factores constantes. Extrayendo todo lo extraíble
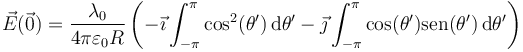
La segunda integral es nula, mientras que la primera vale π. Por tanto, resulta
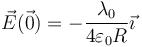
4.3 Potencial en el origen
Para el potencial en el centro aplicamos que cuando tenemos dos cargas iguales y opuestas, el potencial eléctrico en su punto medio es nulo, por estar a la misma distancia de los dos
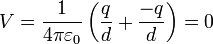
Puesto que en este anillo, para cada elemento de carga su elemento simétrico posee carga igual y de signo contrario, el resultado es que las contribuciones de potencial se anulan mutuamente y

5 Dos superficies esféricas concéntricas
5.1 Carga total
La carga total es la suma de la que hay en cada una de las esferas. A su vez, por ser la densidad uniforme en cada una de ellas

siendo la carga total

5.2 Campo eléctrico
De nuevo tenemos una situación, como en el caso del anillo o del polígono, en que el campo de un punto de la distribución de carga se cancela con el del punto simétrico. Por tanto,
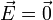
Este resultado puede obtenerse también a partir de un cálculo más general. Aplicando la ley de Gauss se llega a que el campo en todo el interior de la esfera pequeña (y no solo en su centro), es nulo.
5.3 Potencial eléctrico
El potencial eléctrico en todo el volumen puede obtenerse integrando el campo eléctrico, calculado previamente aplicando la ley de Gauss. Sin embargo, para el caso de una superficie esférica, el cálculo del potencial en el centro puede hallarse igualmente por integración directa.
Dada una cierta distribución de carga, el potencial que produce en un punto P es igual a
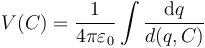
siendo d(q,C) la distancia de cada uno de los elementos de carga al punto C.
Para el caso de una superficie esférica, la distancia al centro es la misma para todos sus puntos. Para la esfera interior
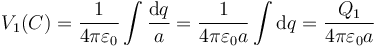
y del mismo modo, el potencial debido a la esfera exterior vale
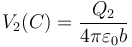
El potencial total en el centro de las dos esferas es la suma de estos dos
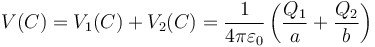
Sustituyendo los valores de cada una de las cargas
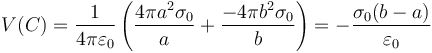
6 Una esfera maciza
6.1 Carga total
En el caso de una distribución volumétrica de carga, la carga total se halla mediante una integral de volumen
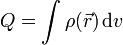
donde la integral se extiende a toda la región donde haya carga. En este caso el volumen es una esfera y la densidad de carga en ella es independiente de la posición por lo que
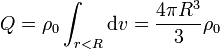
6.2 Campo eléctrico en el centro
Una esfera maciza se puede considerar compuesta de infinitas superficies esféricas concéntricas. Cada una de estas superficies produce un campo nulo en su interior. El campo neto es la suma de todos ellos, por lo que en el centro de la esfera
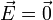
6.3 Potencial eléctrico en el centro
El potencial eléctrico no es nulo. La esfera maciza la consideramos compuesta de capas esféricas. Una superficie esférica de radio r produce un potencial en su centro
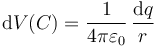
siendo dq la carga de una lámina esférica de área 4πr2 y espesor dr

lo que da la integral para el potencial

Si el dato es la carga total de la esfera

que es un 50% más que para una superficie esférica con carga Q.
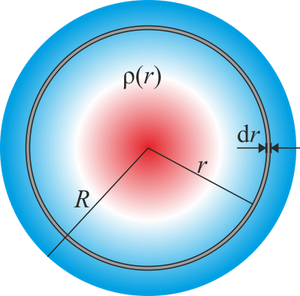
7 Esfera maciza no uniforme
7.1 Carga total
En el último caso tenemos una esfera cuya densidad de carga es positiva entre 0 y R/2, y negativa entre R/2 y R. La carga neta no es nula, ya que la región ocupada por la carga negativa es mayor que la positiva. Si la distribución de carga no es uniforme, sino que depende de la posición, es necesario hallar la integral de volumen
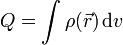
Dividiendo la esfera en capas concéntricas

7.2 Campo en el centro
Como en el caso de la esfera carga uniformemente, esta esfera puede descomponerse en una serie de capas concéntricas, cada una de las cuales posee una densidad uniforme (que puede ser positiva o negativa). Puesto que el campo que produce cada una es nulo en su centro, el campo total también lo es
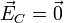
7.3 Potencial eléctrico en el centro
De nuevo, podemos descomponer la esfera en una serie de capas concéntricas, cada una de las cuales produce una contribución al potencial

donde dq, la carga de una lámina esférica, depende de la distancia al centro también a través de la densidad de carga
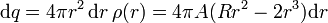
lo que da la integral para el potencial