Algunas identidades vectoriales
De Laplace
Contenido |
1 Enunciado
Demuestre que si  es el vector de posición y
es el vector de posición y  un campo vectorial arbitrario
un campo vectorial arbitrario
Igualmente, para el caso particular en que  represente un vector constante, demuestre que
represente un vector constante, demuestre que
2 Primera identidad (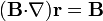 )
)
El operador escalar 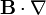 se expresa, en cartesianas, como
se expresa, en cartesianas, como
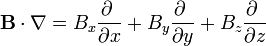
Cuando este operador actúa sobre un campo vectorial, el resultado es la suma de nueve términos, ya que hay que “multiplicar” este operador vectorial por cada una de las componentes del campo vectorial sobre el que actúa:
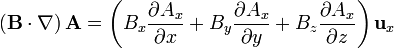
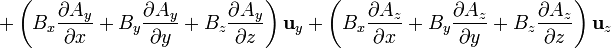
Cuando 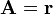 esta expresión se simplifica notablemente, ya que
esta expresión se simplifica notablemente, ya que
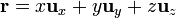
y queda
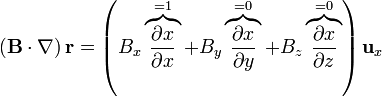
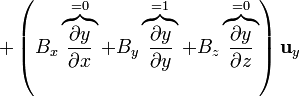
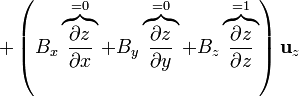
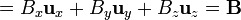
3 Segunda identidad (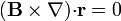 )
)
Este se puede hacer directamente observando que  es un operador vectorial y, por tanto, siempre que no se cambie el orden de los términos y se tenga claro sobre qué actúa, pueden aplicarse las fórmulas del álgebra vectorial. En particular, puede aplicarse la propiedad del producto mixto
es un operador vectorial y, por tanto, siempre que no se cambie el orden de los términos y se tenga claro sobre qué actúa, pueden aplicarse las fórmulas del álgebra vectorial. En particular, puede aplicarse la propiedad del producto mixto
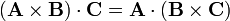
lo que nos convierte nuestra identidad vectorial en
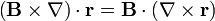
pero el vector de posición es un campo irrotacional. Por tanto
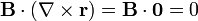
4 Tercera identidad (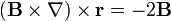 )
)
Una forma de probar esta identidad es escribir, al pie de la letra, lo que expresa, empleando coordenadas cartesianas y suponiendo un vector 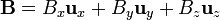 . Si embargo, de esta forma resulta una expresión bastante engorrosa y poco informativa.
. Si embargo, de esta forma resulta una expresión bastante engorrosa y poco informativa.
Podemos acortar este proceso notando que el resultado debe ser una identidad vectorial, independiente del sistema de ejes elegido. Por ello, tenemos libertad para tomar los ejes en la forma que nos resulte más conveniente. Eso sí, el resultado final debe estar expresado de nuevo en una forma independiente de los ejes.
Así pues tomamos el eje Z coincidente con la dirección del campo  , de forma que este se expresa
, de forma que este se expresa
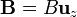
y el operador vectorial 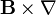 es
es
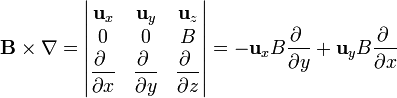
Aplicando ahora este operador vectorial al campo 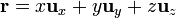 resulta
resulta
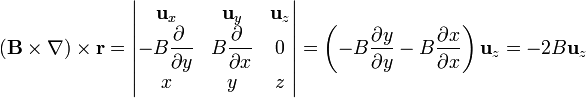
pero 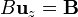 , por tanto
, por tanto
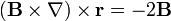
Puesto que este resultado ya no depende de la elección de ejes, es válido para cualquier otra posible elección (si lo hubiéramos dejado como 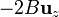 , sí sería dependiente de cuáles son los ejes escogidos).
, sí sería dependiente de cuáles son los ejes escogidos).
5 Cuarta identidad (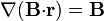 )
)
Como en el apartado anterior, dado que  es un vector constante, elegimos el eje Z de forma que coincida con este vector, con lo que el cálculo se reduce a
es un vector constante, elegimos el eje Z de forma que coincida con este vector, con lo que el cálculo se reduce a
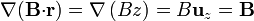
El mismo cálculo se puede hacer sin suponer la dirección de los ejes, pero el proceso es un poco más largo.
6 Quinta identidad (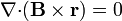 )
)
Aplicando la fórmula general
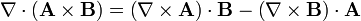
queda
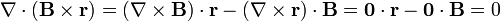
ya que tanto el vector de posición como el campo  (que es un vector constante) son irrotacionales.
(que es un vector constante) son irrotacionales.
7 Sexta identidad (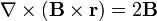 )
)
Aplicando la fórmula general
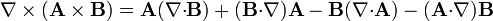
nos queda
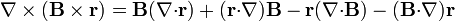
Para el primer término tenemos
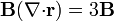
El segundo es nulo, por ser  constante. Lo mismo con el tercero. El cuarto, según la primera identidad es
constante. Lo mismo con el tercero. El cuarto, según la primera identidad es
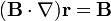
así que queda