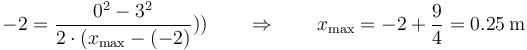Aceleración dependiente de la posición (GIOI)

De Laplace

Contenido

1 Enunciado
2 Velocidad en x = 7 m
3 Velocidad media
4 Caso de aceleración negativa

1 Enunciado

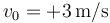Una partícula se mueve sobre una recta partiendo desde $x_0=-5\,\mathrm{m}$ con velocidad $v_0=+3\,\mathrm{m}/\mathrm{s}$ . En su movimiento, experimenta la aceleración

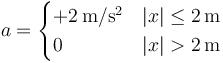
$a=\begin{cases}+2\,\mathrm{m}/\mathrm{s}^2 & |x| \leq 2\,\mathrm{m} \\ 0 & |x| > 2\,\mathrm{m}\end{cases}$

¿Qué velocidad tiene cuando llega al punto $x=+7\,\mathrm{m}$ ?
¿Cuál es la velocidad media en todo el trayecto?
Indique cómo cambian los resultados de los dos apartados anteriores si la aceleración es de la forma

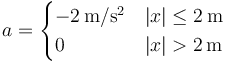
$a=\begin{cases}-2\,\mathrm{m}/\mathrm{s}^2 & |x| \leq 2\,\mathrm{m} \\ 0 & |x| > 2\,\mathrm{m}\end{cases}$

2 Velocidad en x = 7 m

Esta pregunta (y la siguiente) se puede resolver empleando la ecuación del movimiento uniforme y del movimiento uniformemente acelerado, pero también empleando otras que evitan el cálculo en función del tiempo.

La aceleración en un movimiento uniformemente acelerado cumple

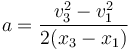
$a = \frac{v_3^2-v_1^2}{2(x_3-x_1)}$

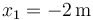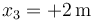La zona donde hay aceleración va de $x_1 = -2\,\mathrm{m}$ a $x_3 = +2\,\mathrm{m}$ , siendo la velocidad de entrada $v 1 = + 3m / s$ y la aceleración +2m/s². Esto nos da, en el SI

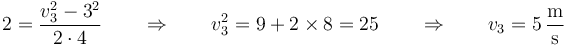
$2 = \frac{v_3^2-3^2}{2\cdot 4}\qquad\Rightarrow\qquad v_3^2 = 9+2\times 8 = 25\qquad\Rightarrow\qquad v_3 = 5\,\frac{\mathrm{m}}{\mathrm{s}}$

A partir de ahí y hasta 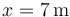$x=7\,\mathrm{m}$ la velocidad es constante e igual a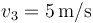 $v_3 = 5\,{\mathrm{m}}/{\mathrm{s}}$

3 Velocidad media

El movimiento se compone de tres tramos, siendo el desplazamiento total

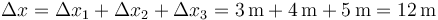
$\Delta x = \Delta x_1 + \Delta x_2 + \Delta x_3 = 3\,\mathrm{m}+4\,\mathrm{m}+5\,\mathrm{m}=12\,\mathrm{m}$

El primer tramo mide 3m y se recorre a una velocidad constante de 3m/s, por lo que

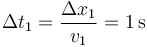
$\Delta t_1 = \frac{\Delta x_1}{v_1}=1\,\mathrm{s}$

El primer tramo mide 5m y se recorre a una velocidad constante de 5m/s, por lo que

$\Delta t_3 = \frac{\Delta x_3}{v_3}=1\,\mathrm{s}$

El segundo tramo se recorre con un movimiento uniformemente acelerado. Para este movimiento la velocidad media es

$v_{m2}=\frac{v_1+v_2}{2}=4\,\frac{\mathrm{m}}{\mathrm{s}}$

y por tanto, el tiempo que se tarda en recorrer esta zona es

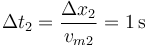
$\Delta t_2 = \frac{\Delta x_2}{v_{m2}}= 1\,\mathrm{s}$

Por tanto, el intervalo total dura

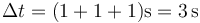
$\Delta t = (1+1+1)\mathrm{s}=3\,\mathrm{s}$

lo que nos da la velocidad media

$v_m = \frac{\Delta x}{\Delta t}=\frac{12\,\mathrm{m}}{3\,\mathrm{s}}=4\,\frac{\mathrm{m}}{\mathrm{s}}$

4 Caso de aceleración negativa

Cuando se aplica la misma lógica del primer apartado al nuevo caso, obtenemos

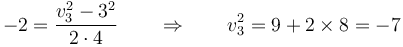
$-2 = \frac{v_3^2-3^2}{2\cdot 4}\qquad\Rightarrow\qquad v_3^2 = 9+2\times 8=-7$

pero este resultado no tiene sentido, ya que sale un cuadrado negativo.

¿Qué ocurre aquí? Que, en este caso, la partícula nunca llega a 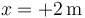$x=+2\,\mathrm{m}$ y, por tanto, tampoco a $x=+7\,\mathrm{m}$ .

Al ser la aceleración negativa, lo que ocurre es que la velocidad de la partícula empieza a disminuir hasta hacerse 0 en un punto de retorno, y a partir de ahí la velocidad se hace negativa, con lo que la partícula vuelve a salir por donde había venido.

El punto de retorno es aquél para el cual la velocidad es cero.

$-2 = \frac{0^2-3^2}{2\cdot (x_\mathrm{max}-(-2)}))\qquad\Rightarrow\qquad x_\mathrm{max} = -2+\frac{9}{4}=0.25\,\mathrm{m}$

Aceleración dependiente de la posición (GIOI)

De Laplace

Contenido

1 Enunciado

2 Velocidad en x = 7 m

3 Velocidad media

4 Caso de aceleración negativa

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES