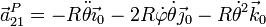No Boletín - Varilla que desliza en aro giratorio

De Laplace

(Redirigido desde 5.9. Varilla que desliza en aro giratorio)

Contenido

1 Enunciado
2 Velocidad y aceleración angular
3 Velocidad y aceleración lineal
- 3.1 Velocidad de P
- 3.2 Aceleración de P

1 Enunciado

El sistema de la figura está constituido por un aro rígido (sólido “0”), de centro C y radio $R$ , que rota libremente alrededor de su diámetro vertical fijo AB contenido en el eje $A Z 1$ del triedro $A X 1 Y 1 Z 1$ (sólido “1”); y por una varilla rígida PQ (sólido “2”), de centro G, cuyos extremos se hallan articulados a sendos deslizadores que los obligan a moverse sobre el aro. Describiendo la cinemática del sistema mediante las derivadas temporales de los ángulos $\varphi$ y $θ$ definidos en la figura, determine:

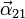$\vec{\omega}_{21}$ , $\vec{\alpha}_{21}$ y eje instantáneo de rotación del movimiento {21}.
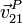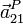$\vec{v}^{P}_{21}$ y $\vec{a}^{P}_{21}$ en el instante en que el extremo P de la varilla pasa por el punto más alto del aro (punto B).

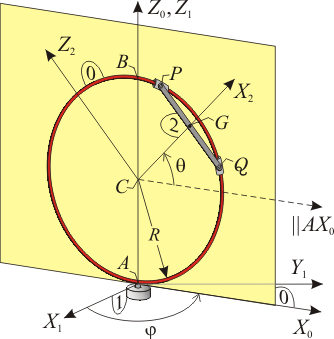
Nota: Para resolver el ejercicio, se recomienda el uso de la base vectorial asociada al triedro “0” de la figura, cuyo plano vertical $A X 0 Z 0$ contiene al aro en todo instante.

2 Velocidad y aceleración angular

2.1 Velocidad angular

De acuerdo con la fórmula de composición de velocidades angulares

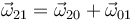
$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}$

Hallamos cada una por separado.

Velocidad angular de arrastre {01}: es la correspondiente a una rotación alrededor de un eje permanente de rotación, en este caso el OZ, por lo que

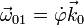
$\vec{\omega}_{01}=\dot{\varphi}\vec{k}_0$

Velocidad angular relativa {20}: la da la variación del ángulo $θ$ . Aunque el segmento CG (con G el punto medio de la varilla) aparentemente no es parte del sólido “2”, es fácil ver que sí se mueve con él y forma parte integral de este sólido. La dirección y sentido de esta velocidad angular la da la regla de la mano derecha, viendo para qué lado gira la varilla cuando $θ$ aumenta

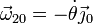
$\vec{\omega}_{20}=-\dot{\theta}\vec{\jmath}_0$

Velocidad angular absoluta {21}: la calculamos como suma de las dos anteriores

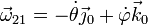
$\vec{\omega}_{21}=-\dot{\theta}\vec{\jmath}_0+\dot{\varphi}\vec{k}_0$

2.2 Aceleración angular

Para la aceleración angular, la ley de composición correspondiente es

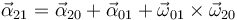
$\vec{\alpha}_{21}=\vec{\alpha}_{20}+\vec{\alpha}_{01}+\vec{\omega}_{01}\times\vec{\omega}_{20}$

Las aceleraciones angulares relativa y de arrastre pueden hallarse simplemente derivando las velocidades angulares correspondientes en el sistema “0”.

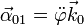
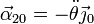
$\vec{\alpha}_{01}=\ddot{\varphi}\vec{k}_0$ $\vec{\alpha}_{20}=-\ddot{\theta}\vec{\jmath}_0$

El término de acoplamiento entre las velocidades angulares vale

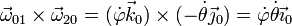
$\vec{\omega}_{01}\times\vec{\omega}_{20}=(\dot{\varphi}\vec{k}_0)\times(-\dot{\theta}\vec{\jmath}_0)=\dot{\varphi}\dot{\theta}\vec{\imath}_0$

Sumando los tres términos obtenemos la aceleración angular absoluta

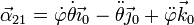
$\vec{\alpha}_{21}=\dot{\varphi}\dot{\theta}\vec{\imath}_0-\ddot{\theta}\vec{\jmath}_0+\ddot{\varphi}\vec{k}_0$

2.3 Eje instantáneo de rotación

El teorema de Varignon afirma que la composición de dos (o más) rotaciones sobre ejes concurrentes (que pasan por un punto común) es otra rotación alrededor de un eje que pasa por el mismo punto. En este caso tenemos que el movimiento de arrastre {01} es una rotación en torno a un eje que pasa por A y B; el movimiento relativo es otra rotación alrededor de un eje paralelo al OY que pasa por C. Ambos ejes de rotación se cortan en C. Por tanto, la composición de ambos es una rotación instantánea en torno a un eje que pasa por C y tiene la dirección marcada por $\vec{\omega}_{21}$ .

En forma vectorial y tomando el origen de coordenadas en el punto A

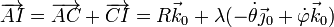
$\overrightarrow{AI}=\overrightarrow{AC}+\overrightarrow{CI}=R\vec{k}_0+\lambda(-\dot{\theta}\vec{\jmath}_0+\dot{\varphi}\vec{k}_0)$

3 Velocidad y aceleración lineal

3.1 Velocidad de P

La velocidad absoluta de P es suma de la relativa más la de arrastre

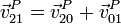
$\vec{v}^P_{21} = \vec{v}^P_{20}+\vec{v}^P_{01}$

Velocidad de arrastre {01}: Por encontrarse instantáneamente sobre el eje permanente de rotación {01}, la velocidad de arrastre es nula

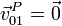
$\vec{v}^P_{01}=\vec{0}$

Velocidad relativa {20}: La velocidad relativa es la debida a un movimiento de rotación en torno a un eje que pasa por C

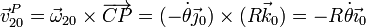
$\vec{v}^P_{20}=\vec{\omega}_{20}\times\overrightarrow{CP}=(-\dot{\theta}\vec{\jmath}_0)\times(R\vec{k}_0)=-R\dot{\theta}\vec{\imath}_0$

Velocidad absoluta {21}: Al ser nula la velocidad de arrastre, la absoluta coincide con la relativa

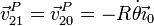
$\vec{v}^P_{21}=\vec{v}^P_{20}=-R\dot{\theta}\vec{\imath}_0$

3.2 Aceleración de P

La aceleración absoluta sigue la ley de composición

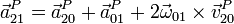
$\vec{a}^P_{21}=\vec{a}^P_{20}+\vec{a}^P_{01}+2\vec{\omega}_{01}\times\vec{v}^P_{20}$

Aceleración de arrastre {01}: Aunque la partícula se encuentre instantáneamente en reposo en el movimiento de arrastre, eso no implica que su aceleración sea nula. Para hallar la aceleración de arrastre empleamos la fórmula para el campo de aceleraciones de un sólido

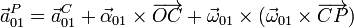
$\vec{a}^P_{01}=\vec{a}^C_{01}+\vec{\alpha}_{01}\times\overrightarrow{OC}+\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{CP})$

siendo C un punto fijo del movimiento. Sin embargo, en el instante considerado en el enunciado, el vector de posición relativa va en la dirección del eje AZ, que es la misma de la velocidad y la aceleración angular de arrastre. Por tanto, los productos vectoriales son nulos y resulta que, efectivamente, su aceleración de arrastre es nula

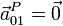
$\vec{a}^P_{01}=\vec{0}$

Aceleración relativa {20}: De nuevo empleamos la expresión para la aceleración de un punto de un sólido rígido

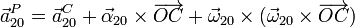
$\vec{a}^P_{20}=\vec{a}^C_{20}+\vec{\alpha}_{20}\times\overrightarrow{OC}+\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{OC})$

resultando la aceleración

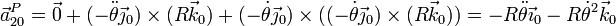
$\vec{a}^P_{20}=\vec{0}+(-\ddot{\theta}\vec{\jmath}_0)\times(R\vec{k}_0)+(-\dot{\theta}\vec{\jmath}_0)\times((-\dot{\theta}\vec{\jmath}_0)\times(R\vec{k}_0))=-R\ddot{\theta}\vec{\imath}_0-R\dot{\theta}^2\vec{k}_0$

Término de Coriolis: Sustituyendo en la expresión de este producto

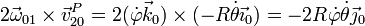
$2\vec{\omega}_{01}\times\vec{v}^P_{20}=2(\dot{\varphi}\vec{k}_0)\times(-R\dot{\theta}\vec{\imath}_0)=-2R\dot{\varphi}\dot{\theta}\vec{\jmath}_0$

Aceleración absoluta {21}: Sumando los tres términos

$\vec{a}^P_{21}=-R\ddot{\theta}\vec{\imath}_0-2R\dot{\varphi}\dot{\theta}\vec{\jmath}_0-R\dot{\theta}^2\vec{k}_0$

No Boletín - Varilla que desliza en aro giratorio

De Laplace

Contenido

1 Enunciado

2 Velocidad y aceleración angular

2.1 Velocidad angular

2.2 Aceleración angular

2.3 Eje instantáneo de rotación

3 Velocidad y aceleración lineal

3.1 Velocidad de P

3.2 Aceleración de P

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES