4.3. Velocidad de tres puntos de un sólido

De Laplace

Contenido

1 Enunciado
2 Valores de las constantes
3 Velocidad en P
4 Velocidad angular y de deslizamiento
- 4.1 Velocidad angular
- 4.2 Velocidad de deslizamiento
5 EIR

1 Enunciado

Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,

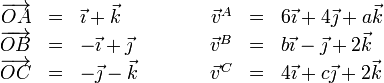
$\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}+\vec{k}&\qquad & \vec{v}^A & = & 6\vec{\imath}+4\vec{\jmath}+a\vec{k}\\ \overrightarrow{OB}&=&-\vec{\imath}+\vec{\jmath}&\qquad & \vec{v}^B& = & b\vec{\imath}-\vec{\jmath}+2\vec{k}\\ \overrightarrow{OC}&=&-\vec{\jmath}-\vec{k}&\qquad & \vec{v}^C&=&4\vec{\imath}+c\vec{\jmath}+2\vec{k} \end{array}$

Halle los valores de $a$ , $b$ , $c$ .
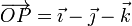Halle la velocidad del punto $\overrightarrow{OP}=\vec{\imath}-\vec{\jmath}-\vec{k}$ .
Calcule la velocidad angular y la de deslizamiento
Determine la posición del eje instantáneo de rotación.

Todas las cantidades están expresadas en las unidades del SI.

2 Valores de las constantes

Podemos hallar las constantes indeterminadas imponiendo la condición cinemática de rigidez, esto es, la equiproyectividad del campo de velocidades:

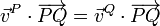
$\vec{v}^P\cdot\overrightarrow{PQ}=\vec{v}^Q\cdot\overrightarrow{PQ}$

En este caso tenemos, para los puntos A y B

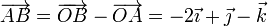
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\vec{\imath}+\vec{\jmath}-\vec{k}$

Proyectando e igualando

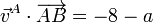
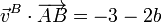
$\vec{v}^A\cdot\overrightarrow{AB}=-8-a$ $\vec{v}^B\cdot\overrightarrow{AB}=-3-2b$ $\Rightarrow$ $-a+2b=5\,$

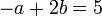
Repitiendo para A y C

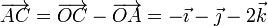
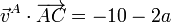
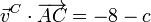
$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}=-\vec{\imath}-\vec{\jmath}-2\vec{k}$ $\vec{v}^A\cdot\overrightarrow{AC}=-10-2a$ $\vec{v}^C\cdot\overrightarrow{AC}=-8-c$ $\Rightarrow$ $-2a+c=2\,$

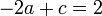
y para B y C

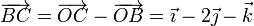
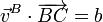
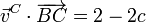
$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=\vec{\imath}-2\vec{\jmath}-\vec{k}$ $\vec{v}^B\cdot\overrightarrow{BC}=b$ $\vec{v}^C\cdot\overrightarrow{BC}=2-2c$ $\Rightarrow$ $b+2c=2\,$

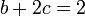
Tenemos el sistema de tres ecuaciones con tres incógnitas

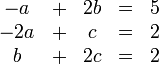
$\begin{matrix} -a&+&2b & = & 5 \\ -2a&+&c & = & 2 \\ b&+&2c & = & 2 \end{matrix}$

con solución

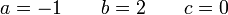
$a=-1\qquad b = 2\qquad c=0$

Las posiciones y velocidades completas de los tres puntos son entonces

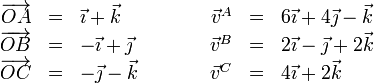
$\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}+\vec{k}&\qquad & \vec{v}^A & = & 6\vec{\imath}+4\vec{\jmath}-\vec{k}\\ \overrightarrow{OB}&=&-\vec{\imath}+\vec{\jmath}&\qquad & \vec{v}^B& = & 2\vec{\imath}-\vec{\jmath}+2\vec{k}\\ \overrightarrow{OC}&=&-\vec{\jmath}-\vec{k}&\qquad & \vec{v}^C&=&4\vec{\imath}+2\vec{k} \end{array}$

Vemos que, aunque para conocer el estado de movimiento de un sólido necesitamos las velocidades de tres de sus puntos, que en total tienen 9 componentes, solo 6 de esas componentes son necesarias, resultando las otras 3 de la condición de rigidez, como corresponde a que un sólido rígido tenga 6 grados de libertad.

3 Velocidad en P

A partir de la velocidad de tres puntos no colineales podemos determinar la velocidad angular y la de deslizamiento del sólido, y a partir de ahí la velocidad de cualquier otro punto. No obstante, también podemos hallar la velocidad de un punto P, no coplanario con A, B y C, a partir de la condición de rigidez. Aplicándola al par formado por P y cada uno de los tres puntos conocidos, tenemos

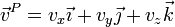
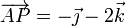
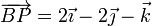
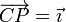
$\vec{v}^P=v_x\vec{\imath}+v_y\vec{\jmath}+v_z\vec{k}$ $\overrightarrow{AP}=-\vec{\jmath}-2\vec{k}$ $\overrightarrow{BP}=2\vec{\imath}-2\vec{\jmath}-\vec{k}$ $\overrightarrow{CP}=\vec{\imath}$

Imponiendo ahora la equiproyectividad

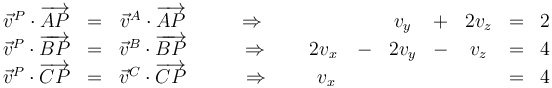
$\begin{matrix} \vec{v}^P\cdot\overrightarrow{AP} & =& \vec{v}^A\cdot\overrightarrow{AP}&\qquad\Rightarrow\qquad \qquad & & v_y & + & 2v_z & = & 2 \\ \vec{v}^P\cdot\overrightarrow{BP} & =& \vec{v}^B\cdot\overrightarrow{BP}&\qquad\Rightarrow\qquad 2v_x & - & 2v_y & - & v_z & = & 4 \\ \vec{v}^P\cdot\overrightarrow{CP} & =& \vec{v}^C\cdot\overrightarrow{CP}&\qquad\Rightarrow\qquad \ v_x & & & & & = & 4 \end{matrix}$

con solución

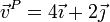
$\vec{v}^P = 4\vec{\imath}+2\vec{\jmath}$

4 Velocidad angular y de deslizamiento

4.1 Velocidad angular

Existen varias formas de determinar la velocidad angular del sólido.

Una de ellas consiste en observar que

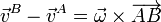
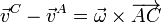
$\vec{v}^B - \vec{v}^A = \vec{\omega}\times\overrightarrow{AB}$ $\vec{v}^C - \vec{v}^A = \vec{\omega}\times\overrightarrow{AC}$

Esto quiere decir que $\vec{\omega}$ es ortogonal a las dos diferencias de velocidades y por tanto va en la dirección de su producto vectorial, esto es,

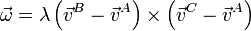
$\vec{\omega}=\lambda\left(\vec{v}^B - \vec{v}^A\right)\times\left(\vec{v}^C - \vec{v}^A \right)$

Sustituyendo

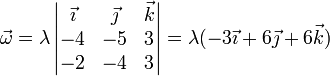
$\vec{\omega}=\lambda\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -4 & -5 & 3 \\ -2 & -4 & 3\end{matrix}\right| =\lambda(-3\vec{\imath}+6\vec{\jmath}+6\vec{k})$

El valor de $λ$ lo obtenemos sustituyendo en alguna de las ecuaciones anteriores

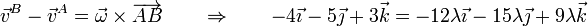
$\vec{v}^B - \vec{v}^A = \vec{\omega}\times\overrightarrow{AB}\qquad\Rightarrow\qquad -4\vec{\imath}-5\vec{\jmath} + 3\vec{k} = -12\lambda\vec{\imath}-15\lambda\vec{\jmath}+9\lambda\vec{k}$

de donde

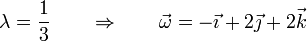
$\lambda = \frac{1}{3}\qquad\Rightarrow\qquad \vec{\omega}=-\vec{\imath}+2\vec{\jmath}+2\vec{k}$

4.2 Velocidad de deslizamiento

Una vez que tenemos la velocidad angular, podemos hallar la velocidad de deslizamiento a partir de la velocidad de cualquier punto del sólido

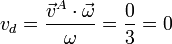
$v_d = \frac{\vec{v}^A\cdot\vec{\omega}}{\omega} = \frac{0}{3}=0$

Esto quiere decir que la velocidad de deslizamiento es nula y por tanto el movimiento instantáneo del sólido es de rotación.

5 EIR

La posición del eje instantáneo de rotación la obtenemos mediante la formula

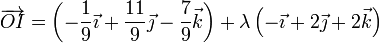
$\overrightarrow{OI}=\overrightarrow{OA}+\overrightarrow{AI}\qquad\qquad\overrightarrow{AI}=\frac{\vec{\omega}\times\vec{v}^A}{\omega^2}+\lambda\vec{\omega}$ $\Rightarrow$ $\overrightarrow{OI} =\left(-\frac{1}{9}\vec{\imath}+\frac{11}{9}\vec{\jmath}-\frac{7}{9}\vec{k}\right)+\lambda\left(-\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)$

Esta ecuación queda un poco más corta haciendo

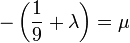
$-\left(\frac{1}{9}+\lambda\right) = \mu$

y nos queda

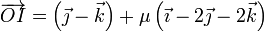
$\overrightarrow{OI}=\left(\vec{\jmath}-\vec{k}\right)+\mu\left(\vec{\imath}-2\vec{\jmath}-2\vec{k}\right)$

Otra posibilidad consiste en buscar aquellos puntos cuya velocidad es nula (por tratarse de una rotación). Esto nos da

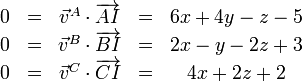
$\begin{matrix} 0 & = & \vec{v}^A\cdot\overrightarrow{AI} & = & 6x+4y-z-5\\ 0 & = & \vec{v}^B\cdot\overrightarrow{BI} & = & 2x-y-2z+3\\ 0 & = & \vec{v}^C\cdot\overrightarrow{CI} & = & 4x+2z+2 \end{matrix}$

La solución de estas ecuaciones conduce a unas ecuaciones paramétricas equivalentes a la ecuación vectorial anterior.

4.3. Velocidad de tres puntos de un sólido

De Laplace

Contenido

1 Enunciado

2 Valores de las constantes

3 Velocidad en P

4 Velocidad angular y de deslizamiento

4.1 Velocidad angular

4.2 Velocidad de deslizamiento

5 EIR

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES