1.3. Lados de un triángulo rectángulo (Ex.Nov/11)
De Laplace
1 Enunciado
¿Cuál de las siguientes ternas de vectores libres podría corresponder a los tres lados de un triángulo rectángulo?
- (1)
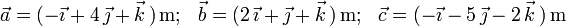
- (2)

- (3)
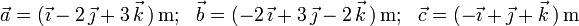
- (4)
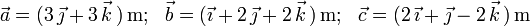
2 Solución
Los lados de un triángulo constituyen una línea poligonal cerrada. Por tanto, tres vectores libres (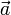 ,
, 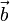 y
y 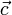 ) sólo podrán corresponder a los lados de un triángulo si admiten una ordenación que les haga formar una línea poligonal cerrada. Dependiendo de los sentidos relativos de los vectores en dicha poligonal cerrada, existen cuatro situaciones posibles, cada una de las cuales corresponde al cumplimiento de una de las cuatro ecuaciones siguientes:
) sólo podrán corresponder a los lados de un triángulo si admiten una ordenación que les haga formar una línea poligonal cerrada. Dependiendo de los sentidos relativos de los vectores en dicha poligonal cerrada, existen cuatro situaciones posibles, cada una de las cuales corresponde al cumplimiento de una de las cuatro ecuaciones siguientes:

Es inmediato comprobar que las ternas (2) y (4) del enunciado no satisfacen ninguna de estas ecuaciones, de modo que quedan descartadas. Sin embargo, la terna (1) satisface 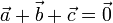 , y la terna (3) satisface
, y la terna (3) satisface 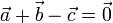 .
.
Ahora bien, para que el triángulo formado sea rectángulo es necesario además que dos de los vectores de la terna sean ortogonales, lo cual no ocurre en la terna (1). Por el contrario, en la terna (3) observamos que 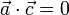 . Así que concluimos que la única terna de vectores libres que podría corresponder a los tres lados de un triángulo rectángulo es la (3).
. Así que concluimos que la única terna de vectores libres que podría corresponder a los tres lados de un triángulo rectángulo es la (3).





