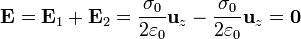Campo debido a dos planos paralelos
De Laplace
Revisión a fecha de 20:27 8 ene 2010; Antonio (Discusión | contribuciones)
1 Enunciado
Un condensador de placas planas puede aproximarse por dos dos planos paralelos, separados una distancia a. Uno de ellos, situado en z = − a / 2 posee una distribución de carga uniforme σ0, mientras que la del otro, situado en z = a / 2 es − σ0. Halle el campo eléctrico en todos los puntos del espacio.
2 Solución
Este problema puede resolverse por simple superposición de los campos de los planos individuales.
El campo debido a un plano cargado uniformenente situado en z = 0 es
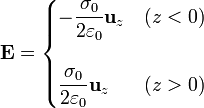
Si este plano está en z = − a / 2 simplemente trasladamos la coordenada y ya tenemos el campo del primer plano
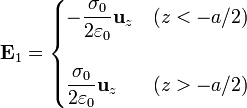
Para el segundo plano, cambiamos a por − a y σ0 por − σ0, lo que nos deja
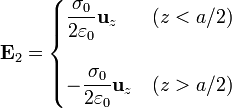
Para superponer estos campos, dividimos el espacio en tres regiones:
- Por debajo del plano inferior (z < − a / 2)
- En esta zona los campos son iguales y opuestos
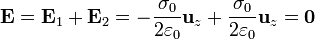
- Por debajo del plano inferior ( − a / 2 < z < a / 2)
- En esta zona los campos son iguales y en el mismo sentido
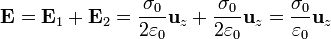
- Por encima del plano superior (z > a / 2)
- En esta zona, de nuevo, los campos son iguales y opuestos