Superficies esféricas concéntricas cargadas

De Laplace

Revisión a fecha de 14:57 7 ene 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Campo eléctrico y cargas
- 2.1 Campo eléctrico
- 2.2 Densidades de carga
3 Potencial y energía
- 3.1 Potencial de las esferas
- 3.2 Energía electrostática
4 Estado tras la conexión
- 4.1 Campo eléctrico
- 4.2 Potencial eléctrico
5 Variación en la energía

1 Enunciado

Dos superficies conductoras ideales, esféricas y concéntricas de radios

a

y

2 a

y espesor despreciable, están cargadas eléctricamente de manera uniforme, siendo

σ 0

y

+ σ 0

los valores netos de las respectivas densidades superficiales de carga.

Obtenga las expresiones del campo eléctrico en las regiones interior, intermedia y exterior a las dos esferas. Determine cómo son las densidades superficiales de carga eléctrica en las caras interior y exterior de cada una de las superficies conductoras.
Calcule el valor del potencial eléctrico en dichas superficies, así como la energía electrostática almacenada por el sistema.
Suponga que se conectan las superficies por un fino hilo conductor. En la nueva situación de equilibrio, ¿cuánto valen el campo eléctrico y el potencial en todo el espacio?
Calcule la variación en la energía electrostática almacenada, como consecuencia de la conexión anterior. ¿Cómo se explica este cambio en la energía?

2 Campo eléctrico y cargas

2.1 Campo eléctrico

El campo eléctrico en todo el espacio lo podemos hallar por simple aplicación de la ley de Gauss. Dada la simetría de revolución del sistema, podemos suponer que el potencial eléctrico depende exclusivamente de la distancia $r$ al centro del sistema y el campo eléctrico es, por tanto, central

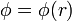
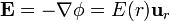
$\phi = \phi(r)\,$ $\Rightarrow$ $\mathbf{E}=-\nabla\phi = E(r)\mathbf{u}_r$

En este caso, el flujo del campo eléctrico a través de una superficie esférica concéntrica con las dos esferas de carga es

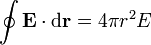
$\oint \mathbf{E}\cdot\mathrm{d}\mathbf{r}=4\pi r^2 E$

De acuerdo con la ley de Gauss, este flujo es igual a la carga encerrada dividida por la permitividad del vacío

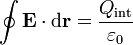
$\oint \mathbf{E}\cdot\mathrm{d}\mathbf{r}=\frac{Q_\mathrm{int}}{\varepsilon_0}$ $\Rightarrow$ $\mathbf{E}(r) = \frac{Q_\mathrm{int}(r)}{4\pi\varepsilon_0 r^2}\mathbf{u}_r$

La carga encerrada depende del tamaño de la superficie de integración. Tenemos tres casos

Región interior ( $r < a$ ): En esta zona, una superficie esférica no encierra carga alguna, por tanto

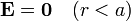
$Q_\mathrm{int}(r)=0\,$ $\Rightarrow$ $\mathbf{E}=\mathbf{0}\quad (r<a)$

Región intermedia ( $a < r < 2 a$ ): En este caso, la carga encerrada es la de la esfera interior. Por ser la distribución de carga uniforme, la carga de esta esfera es

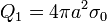
$Q_1 = 4\pi a^2 \sigma_0\,$

y el campo eléctrico resultante

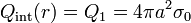
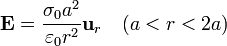
$Q_\mathrm{int}(r)=Q_1 = 4\pi a^2\sigma_0\,$ $\Rightarrow$ $\mathbf{E}=\frac{\sigma_0a^2}{\varepsilon_0 r^2}\mathbf{u}_r\quad (a<r<2a)$

Región exterior ( $r > 2 a$ ): En esta región, la carga encerrada es la de la de las dos esferas conjuntamente. La carga de la esfera exterior es, por ser la distribución de nuevo uniforme,

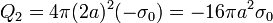
$Q_2 = 4\pi (2a)^2(-\sigma_0)=-16\pi a^2\sigma_0\,$

y el campo eléctrico resultante

$Q_\mathrm{int}(r)=Q_1+ Q_2 = -12\pi a^2\sigma_0\,$ $\Rightarrow$ $\mathbf{E}=-\frac{3\sigma_0a^2}{\varepsilon_0 r^2}\mathbf{u}_r\quad(r>2a)$

Vemos que el campo exterior no es nulo, por ser la carga neta distinta de cero, ya que la carga negativa de la esfera exterior es más grande que la positiva de la interior.

2.2 Densidades de carga

3 Potencial y energía

3.1 Potencial de las esferas

3.2 Energía electrostática

4 Estado tras la conexión

4.1 Campo eléctrico

4.2 Potencial eléctrico

5 Variación en la energía

Superficies esféricas concéntricas cargadas

De Laplace

Contenido

1 Enunciado

2 Campo eléctrico y cargas

2.1 Campo eléctrico

2.2 Densidades de carga

3 Potencial y energía

3.1 Potencial de las esferas

3.2 Energía electrostática

4 Estado tras la conexión

4.1 Campo eléctrico

4.2 Potencial eléctrico

5 Variación en la energía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES