Imán en forma de tubo

De Laplace

Revisión a fecha de 18:17 10 sep 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Corrientes de imanación
3 Cargas magnéticas
4 Campo en el centro
5 Aproximación dipolar

1 Enunciado

Se tiene un tubo cilíndrico imanado longitudinalmente con una magnetización uniforme 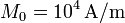$M_0 = 10^4\,\mathrm{A}/\mathrm{m}$ . El tubo posee una longitud $h = 24\,\mathrm{mm}$ , un radio interior $a = 9\,\mathrm{mm}$ y uno exterior $b = 16\,\mathrm{mm}$

Calcule las corrientes de imanación equivalentes a este imán.
Halle las cargas de imanación equivalentes.
Calcule el valor exacto del campo magnético en el centro del tubo.
Halle el momento dipolar del imán y calcule el valor aproximado del campo magnético en un punto situado a 10 cm en la dirección del eje.

2 Corrientes de imanación

Las corrientes de imanación equivalentes a la magnetización pueden ser volumétricas y superficiales.

2.1 Corrientes de volumen

La densidad de volumétrica de corrientes de magnetización es

$\mathbf{J}_m = \nabla\times\mathbf{M}$

Esta densidad es nula tanto en el exterior del imán (porque fuera la magnetización es nula), como en su interior (porque es uniforme)

$\mathbf{J}_m = \nabla\times\mathbf{M}=\begin{cases}\nabla\times\mathbf{M}_0=\mathbf{0} & \mathrm{interior}\\ \nabla\times\mathbf{0}=\mathbf{0} & \mathrm{exterior}\end{cases}$

Por tanto las únicas densidades de corriente serán superficiales.

2.2 Corrientes superficiales

Tenemos cuatro superficies diferentes: las dos bases, la cara interior y la exterior. Para cada una de ellas, la densidad superficial de corriente imanación es de la forma

$\mathbf{K}_m=\mathbf{n}\times[\mathbf{M}]$

Empleando coordenadas cilíndricas y tomando el eje Z como del del tubo, la imanación se escribe

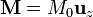
$\mathbf{M}=M_0\mathbf{u}_z\,$

y el vector $\mathbf{n}$ depende de la superficie en cuestión.

Analizando por separado cada superficie:

2.2.1 Base superior

En la cara superior

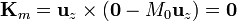
$\mathbf{n}=\mathbf{u}_z\,$ $\Rightarrow$ $\mathbf{K}_m=\mathbf{u}_z\times(\mathbf{0}-M_0\mathbf{u}_z)=\mathbf{0}$

Al ser la magnetización paralela al vector normal, la densidad superficial es nula.

2.2.2 Base inferior

En la cara inferior el cálculo es casi idéntico. Tomando

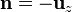
$\mathbf{n}=-\mathbf{u}_z\,$ $\Rightarrow$ $\mathbf{K}_m=(-\mathbf{u}_z)\times(\mathbf{0}-M_0\mathbf{u}_z)=\mathbf{0}$

La densidad superficial es nula en esta cara.

2.2.3 Cara exterior

En la cara lateral exterior, el vector normal es 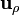$\mathbf{u}_\rho$ por lo que la corriente superficial vale

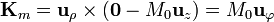
$\mathbf{n}=\mathbf{u}_\rho\,$ $\Rightarrow$ $\mathbf{K}_m=\mathbf{u}_\rho\times(\mathbf{0}-M_0\mathbf{u}_z)=M_0\mathbf{u}_\varphi$

La densidad superficial va en la dirección acimutal, girando en torno a la imanación, en sentido antihorario.

2.2.4 Cara interior

En la cara lateral interior, tomamos como vector normal 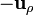$-\mathbf{u}_\rho$ y resulta la corriente superficial

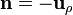
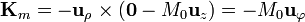
$\mathbf{n}=-\mathbf{u}_\rho\,$ $\Rightarrow$ $\mathbf{K}_m=-\mathbf{u}_\rho\times(\mathbf{0}-M_0\mathbf{u}_z)=-M_0\mathbf{u}_\varphi$

Resulta una densidad también acimutal, pero en sentido opuesto a la anterior.

2.3 Sistema de corrientes equivalente

Reuniendo los resultados anteriores resulta que el imán en forma de tubo equivale a dos distribuciones superficiales, que fluyen sobre sendos cilindros de radios $a$ y $b$ , en sentidos opuestos, esto es, el imán equivale a dos solenoides por los que circula la misma densidad de corriente, pero arrollados en sentidos opuestos.

3 Cargas magnéticas

Las densidades de carga magnética equivalentes a la magnetización pueden ser también volumétricas y superficiales.

3.1 Densidad volumétrica de carga

La densidad volumétrica de cargas magnéticas es

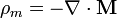
$\rho_m = -\nabla\cdot\mathbf{M}$

Esta densidad es nula tanto en el exterior del imán (porque fuera la magnetización es nula), como en su interior (porque es uniforme)

$\rho_m = -\nabla\cdot\mathbf{M}=\begin{cases}-\nabla\cdot\mathbf{M}_0=0 & \mathrm{interior}\\ -\nabla\cdot\mathbf{0}=0 & \mathrm{exterior}\end{cases}$

Por tanto las únicas densidades de carga serán superficiales.

3.2 Densidades superficiales

La densidad superficial de carga magnética equivalente tiene la forma general

$\sigma_m=-\mathbf{n}\cdot[\mathbf{M}]$

Analizando por separado cada una de las cuatro superficies:

3.2.1 Base superior

En la cara superior

$\mathbf{n}=\mathbf{u}_z\,$ $\Rightarrow$ $\sigma_m=-\mathbf{u}_z\cdot(\mathbf{0}-M_0\mathbf{u}_z)=M_0$

Existe una densidad de carga positiva en esta cara, que corresponde al polo norte del imán.

3.2.2 Base inferior

En la cara inferior el cálculo es casi idéntico. Tomando

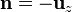
$\mathbf{n}=-\mathbf{u}_z\,$ $\Rightarrow$ $\rho_m=(-\mathbf{u}_z)\cdot(\mathbf{0}-M_0\mathbf{u}_z)=-M_0$

Resulta ahora una densidad negativa, correspondiente al polo sur del imán.

3.2.3 Cara exterior

En la cara lateral exterior, el vector normal es 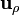$\mathbf{u}_\rho$ por lo que la densidad de carga superficial vale

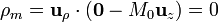
$\mathbf{n}=\mathbf{u}_\rho\,$ $\Rightarrow$ $\rho_m=\mathbf{u}_\rho\cdot(\mathbf{0}-M_0\mathbf{u}_z)=0$

En esta superficie la densidad de carga es nula, por ser el vector normal ortogonal a la imanación.

3.2.4 Cara interior

En la cara lateral interior, tomamos como vector normal 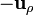$-\mathbf{u}_\rho$ y resulta la densidad superficial

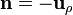
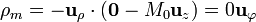
$\mathbf{n}=-\mathbf{u}_\rho\,$ $\Rightarrow$ $\rho_m=-\mathbf{u}_\rho\cdot(\mathbf{0}-M_0\mathbf{u}_z)=0\mathbf{u}_\varphi$

De nuevo la densidad es nula, por la misma razón que en el caso anterior.

3.3 Sistema de cargass equivalente

Reuniendo los resultados anteriores resulta que el imán en forma de tubo equivale a dos distribuciones superficiales de carga, ambas en forma de corona circular de radio interior $a$ y exterior $b$ situadas paralelamente a una distancia $h$ .

4 Campo en el centro

5 Aproximación dipolar