Condensador con tres capas de dieléctrico
De Laplace
Contenido |
1 Enunciado
Entre dos placas metálicas, planas y paralelas de sección S y separadas una distancia 3a se encuentran tres capas de dieléctrico, de espesor a cada una. Las capas poseen permitividades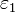 ,
, 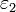 y
y 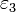 . Las dos capas adyacentes a las placas son dieléctricos ideales, mientras que la capa central posee una conductividad σ.
. Las dos capas adyacentes a las placas son dieléctricos ideales, mientras que la capa central posee una conductividad σ.
Se establece bruscamente una diferencia de potencial V0 entre las placas conductoras
- Determine la distribución del campo eléctrico en todos los puntos entre las placas, en los instantes inmediatamente posteriores a la conexión.
- Calcule la energía electrostática almacenada en el sistema en estos instantes iniciales.
- Pasado un tiempo largo tras la conexión, ¿cuál es la distribución de campos en el sistema? ¿Cuánto vale la energía almacenada?
- ¿Cuánto valen las cargas almacenadas en las placas inmediatamente después de la conexión y mucho tiempo después de ella? ¿Qué trabajo ha realizado el generador en el periodo transitorio?
- Sin resolver la evolución temporal de los campos en el sistema, ¿cuánto vale la energía disipada durante el periodo transitorio?
Desprecie los efectos de borde.
2 Introducción
Este problema requiere algunos conceptos de corriente eléctrica pero su solución matemática puede hacerse de forma completa empleando exclusivamente conductores perfectos y dieléctricos ideales.
La idea es que, inmediatamente tras la conexión, no ha dado tiempo a que las cargas se redistribuyan en el material con conductividad (aunque sí en las placas, que son conductores perfectos), de forma que las tres capas se comportan como dieléctricos ideales.
Mucho tiempo tras la conexión, la capa central, conductora, alcanza el equilibrio electrostático y se convierte en equipotencial y el sistema se reduce a solo dos capas de dieléctrico, con un conductor entre ellas.
Este sistema puede resolverse de numerosas formas
- Resolviendo el problema para el potencial eléctrico
- Empleando solamente el campo eléctrico y el vector desplazamiento.
- Usando un circuito equivalente.
Aquí veremos la solución a partir del campo y el desplzamiento; al final comentaremos cómo sería con el circuito equivalente.
3 Situación tras la conexión
La solución de este apartado es una generalización del condensador con dos capas de dieléctrico.
En el instante inmediatamente posterior a la conexión, se establece una diferencia de potencial entre las placas exteriores, que se cargan inmediatamente. Esta diferencia de potencial implica un campo eléctrico en las tres regiones, que no tiene por qué ser el mismo en cada una.
En cada una de las capas, por tratarse de medios homogéneos, no hay carga de volumen y se cumplen las ecuaciones diferenciales
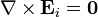
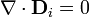
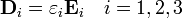
Como en el caso del condensador con dos capas de dieléctrico, si despreciamos los efectos de borde, esto implica que los campos son uniformes en cada región
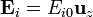
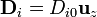
Los valores de estas constantes los obtenemos las condiciones de salto. En el instante t = 0 + aun no se ha acumulado carga en las interfaces entre las capas, de forma que se verifica la continuidad de la componente normal de 
![\mathbf{n}\cdot[\mathbf{D}]=\sigma_s=0\,](/wiki/images/math/4/f/d/4fd83ae610277a101ab2cc8c32f0b2e2.png)

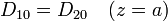
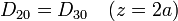
De aquí tenemos que el vector desplazamiento tiene el mismo valor en las tres capas
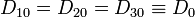
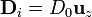


El valor de D0 lo sacamos de que conocemos la diferencia de potencial entre las placas
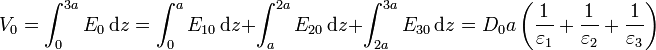
Despejando de aquí

y el campo eléctrico en cada región será
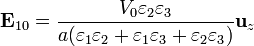
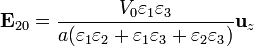
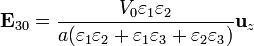
4 Energía inicial
Una vez que tenemos el campo en cada región, la energía es inmediata
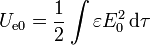
Descomponiendo en las tres regiones
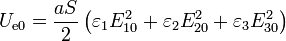
podemos sustituir aquí las expresiones, pero es un poco más simple si observamos que
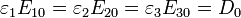

y por tanto
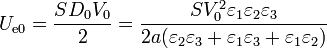
5 Estado final
Cuando ha pasado mucho tiempo tras la conexión, la banda central, que es conductora, alcanza el equilibrio electrostático. Una cierta cantidad de carga negativa se ha movido en la dirección opuesta al campo y una positiva aparece en el sentido del campo. Esta carga anula el campo en el interior de este material, de forma que en el estado final tenemos
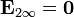
Para hallar 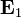 y
y 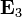 tenemos que la diferencia de potencial entre las placas sigue siendo V0
tenemos que la diferencia de potencial entre las placas sigue siendo V0
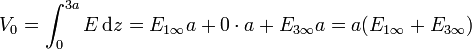
Necesitamos una ecuación adicional. Ésta la sacamos de la ley de conservación de la carga. El conductor central está aislado, por lo que la carga central en él permanece constante. Puesto que inicialmente estaba descargado, la cantidad de carga positiva que aparece en un lado debe cancelarse exactamente con la negativa en el otro. Imponemos que la carga total es cero con
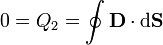
El flujo del vector desplazamiento se compone de dos contribuciones, una en el medio 1 y otra en el 3



resulta el mismo valor del vector desplzamiento en ambas regiones. Por tanto
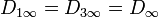

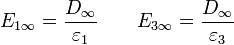
Sustituyendo en la diferencia de potencial obtenemos 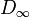
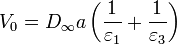

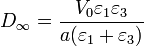
El campo eléctrico en cada región es, en el estado estacionario final

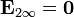
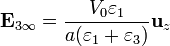
La energía en el estado final es
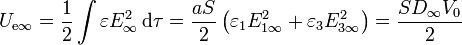
Sustituyendo los valores queda
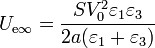
Esta enegría es mayor que la inicial, ya que

6 Cargas en las placas
La carga en las placas conductoras la obtenemos a partir del flujo del vector desplazamiento a través de una superficie que las envuelve.
6.1 Tras la conexión
Para la placa a potencial V0 tenemos,
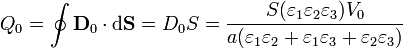
mientras que la placa a tierra tiene una carga exactamente igual y de signo contrario.
6.2 En el estado estacionario
Mucho tiempo tras la conexión, la nueva carga almacenada es
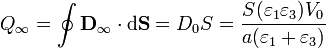
6.3 Trabajo del generador
La carga inicial y la final no son iguales, lo que quiere decir que el generador realiza un trabajo durante el periodo transitorio para aportar o retirar el exceso de carga. Dado que el generador proporciona una tensión constante, este trabajo es igual a la cantidad de carga multiplicada por el potencial al que se pone.
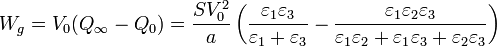
Multiplicando en el primer término por 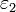 en el numerador y en el denominador queda
en el numerador y en el denominador queda

Este trabajo es positivo, ya que la carga de la placa aumenta durante el periodo transitorio.
7 Energía disipada
Podemos hallar la energía disipada en el periodo transitorio sin necesidad de hallar la corriente y la potencia debida al efecto Joule. Nos basta con un balance energético.
Tenemos una energía inicial Ue0 y un trabajo realizado por el generador Wg. La suma de estos dos (la energía que ya había más la que aporta el generador), nos debería dar la energía final. Sin embargo, la energía final 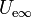 es inferior a esta suma. La diferencia es la energía disipada por el camino. Por tanto
es inferior a esta suma. La diferencia es la energía disipada por el camino. Por tanto

Tenemos que
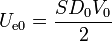
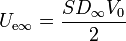
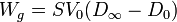
y, por tanto,
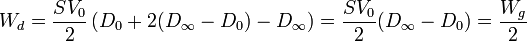
esto es, la mitad del trabajo realizado por el generador se va en energía disipada (y la otra mitad queda como energía almacenada). Sustituyendo

8 Solución mediante un circuito equivalente
Este problema puede resolverse empleando un circuito equivalente. Cada capa de dieléctrico se puede modelar por un condensador ideal de capacidad
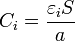
Además, para la capa central, que posee conductividad, debemos añadir una resistencia en paralelo, de valor
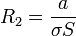
Esta resistencia está en paralelo con el condensador correspondiente. Esta asociación se encuentra en serie con los condensadores C1 y C3.
La diferencia de potencial se establece entre los extremos del conjunto.
Inmediatamente tras la conexión, se cargan los tres condensadores. Durante el periodo transitorio, el condensador central se va descargando a través de la resistencia, mientras los otros dos aumentan su carga de forma que la diferencia de potencial se mantiene constante. En el estado estacionario final, el condensador central está descargado y funciona como un cortocircuito, de forma que el sistema se reduce a una asociación en serie de los dos condensadores.
8.1 Cargas, energía y campos iniciales
En t = 0 + , tenemos una asociación de tres condensadores cuya capacidad equivalente verifica

de forma que la carga inicial en la placa conductora a tensión V0 es
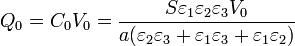
La energía almacenada en el sistema inicialmente es
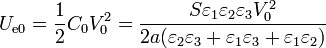
El campo eléctrico en cada región lo obtenemos hallando previamente la diferencia de potencial en cada condensador como
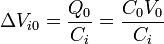
y de aquí hallamos el campo
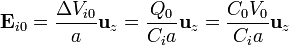
Sustituyendo queda
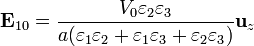
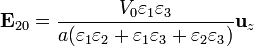
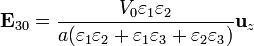
8.2 Carga, energía y campos finales
En el estado final, el condensador C2 está cortocircuitado y el sistema se reduce a la asociación en serie de C1 y C3
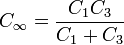
y de aquí obtenemos la carga final
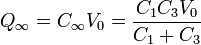
la energía
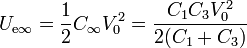
y los campos en el estado final
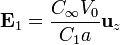
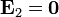
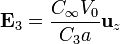
9 =Balance energético
El trabajo realizado por el generador es
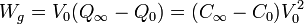
por lo que la energía disipada es

Sustituyendo se obtiene el resultado que ya conocemos.






