Resistencia de un tubo

De Laplace

Revisión a fecha de 12:35 2 sep 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Resistencia longitudinal
4 Resistencia transversal

1 Enunciado

Sea un tubo cilíndrico, de radio interior

a

y exterior

b

, y longitud

h

, de un material de conductividad

σ

. Calcule la resistencia eléctrica

Entre las dos bases.
Entre la cara interior y la exterior.

2 Introducción

A la hora de hablar de la resistencia de un conductor, tan importante como dar las dimensiones de la pieza es definir de dónde a dónde fluye la corriente. Hay veces en que esto es evidente (por ejemplo, en un conductor filiforme, parece natural que la corriente fluya de un extremo al otro), pero no siempre es así.

Consideremos un cilindro hueco como en este problema.

Este cilindro puede ser parte de un cable bimetálico, por ejemplo, un cable de cobre con un núcleo de acero para darle rigidez, como los que se emplean en algunos tendidos de gran longitud. En este cable bimetálico, la corriente fluye a lo largo del cobre principalmente (pues el acero es mucho más resistivo) y debemos considerar la resistencia entre las bases.

Alternativamente, este cilindro puede representar el dieléctrico que se encuentra entre los conductores de un cable coaxial. Este dieléctrico se supone perfectamente aislante, pero en realidad suele tener una pequeña conductividad. En este caso, existen corrientes de fuga que van desde el conductor interior al exterior, radialmente. La resistencia del cilindro debe calcularse entre su superficie interior y la exterior.

Tanto en un caso como el otro, las ecuaciónes que verifican el campo eléctrico y la corriente son:

El campo eléctrico es irrotacional, por tratarse de una situación estacionaria, lo que permite usar el potencial eléctrico

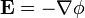
$\nabla\times\mathbf{E}=\mathbf{0}$ $\Rightarrow$ $\mathbf{E}=-\nabla\phi$

La densidad de corriente es solenoidal, por tratarse de una distribución estacionaria,

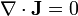
$\nabla\cdot\mathbf{J}=0$

Se cumple la ley de Ohm

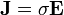
$\mathbf{J}=\sigma\mathbf{E}\,$

Combinando estas ecuaciones obtenemos que, si el material es homogéneo (la conductividad no depende de la posición), el potencial verifica la ecuación de Laplace

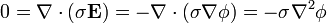
$0 = \nabla\cdot(\sigma\mathbf{E})=-\nabla\cdot(\sigma\nabla\phi)=-\sigma\nabla^2\phi$ $\Rightarrow$ $\nabla^2\phi = 0$

La técnica para hallar la resistencia entre dos superficies entre las cuales hay un material homogéneo, consiste en:

Suponer una cierta diferencia de potencial $V 0$ entre estas superficies.

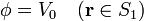
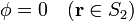
$\phi = V_0\quad (\mathbf{r}\in S_1)$ $\phi=0\quad(\mathbf{r}\in S_2)$

Suponer que el por resto de las paredes no entra ni sale corriente, esto es, hay un tubo de corriente de una superficie a la otra.

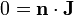
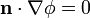
$0 = \mathbf{n}\cdot\mathbf{J}$ $\Rightarrow$ $\mathbf{n}\cdot\nabla\phi=0$

Resolver la ecuación de Laplace con estas condiciones de contorno.
Hallar el campo eléctrico a partir del potencial.
Hallar la densidad de corriente mediante la ley de Ohm.
Calcular el flujo de la densidad de corriente a través de la superficie puesta a potencial $V 0$ . Este flujo es la intensidad de corriente.
Dividir la diferencia de potencial entre la intensidad de corriente; el resultado es la resistencia eléctrica.

Si el material no es homogéneo ya el potencial eléctrico no verifica la ecuación de Laplace y puede resultar conveniente prescindir de él y trabajar directamente con la densidad de corriente y el campo eléctrico.

3 Resistencia longitudinal

En el caso de la resistencia longitudinal, la diferencia de potencial se estable entre las bases, por lo que las correspondientes condiciones de contorno son

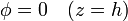
$\phi = V_0\quad (z=0)$ $\phi=0\quad(z=h)$

La condición de que la corriente no escape por las paredes laterales se expresa

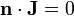
$\mathbf{n}\cdot\mathbf{J}=0$ $\Rightarrow$ \mathbf{n}\cdot\nabla\phi=0

Empleando coordenadas cilíndricas con $z$ la dirección longitudinal queda

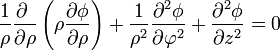
$\frac{1}{\rho}\frac{\partial{}\ }{\partial{}\rho}\left(\rho\frac{\partial{}\phi}{\partial{}\rho}\right) +\frac{1}{\rho^2}\frac{\partial^2\phi}{\partial\varphi^2}+\frac{\partial^2\phi}{\partial z^2}=0$

A esta ecuación debemos añadir las condiciones de contorno de que en los extremos haya una diferencia de potencial $V 0$ ,

$\phi=V\qquad (z=0)\qquad\phi=0\qquad (z=h)$

Además de estas condiciones hay que fijar las condiciones en las paredes laterales. En estas se verifica que la corriente que sale es nula (no hay fugas) y, por tanto,

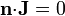
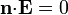
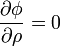
$\mathbf{n}{\cdot}\mathbf{J}=0$ $\Rightarrow$ $\mathbf{n}{\cdot}\mathbf{E}=0$ $\Rightarrow$ $\frac{\partial{}\phi}{\partial{}\rho}=0$

esto es, en las caras laterales se cumple que la derivada del potencial en la dirección perpendicular (radial en este caso) es nula.

Una solución para este problema es un potencial que varía linealmente con $z$

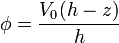
$\phi=\frac{V_0(h-z)}{h}$

Este potencial obedece la ecuación de Laplace y satisface las condiciones de contorno tanto en las bases como en las caras laterales. por tanto, es la solución.

Conocido el potencial, hallamos el campo y la corriente

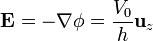
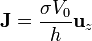
$\mathbf{E}=-\nabla\phi=\frac{V_0}{h}\mathbf{u}_{z}$ $\mathbf{J}=\frac{\sigma V_0}{h}\mathbf{u}_{z}$

Resulta un campo y una corriente uniformes en la dirección longitudinal.

Integrando ahora sobre una sección transversal resulta

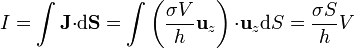
$I=\int \mathbf{J}{\cdot}\mathrm{d}\mathbf{S}=\int \left(\frac{\sigma V}{h}\mathbf{u}_{z}\right){\cdot}\mathbf{u}_{z}\mathrm{d}S=\frac{\sigma S}{h}V$

de donde la resistencia es

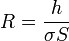
$R=\frac{h}{\sigma S}$

4 Resistencia transversal

Tenemos dos superficies concéntricas a diferente potencial. La corriente fluirá de la interior a la exterior verificándose la ecuación de Laplace, por tratarse de corrientes estacionarias

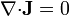
$\nabla{\cdot}\mathbf{J} = 0$ $\Rightarrow$ $\nabla^2\phi = 0$

con las condiciones de contorno

$\phi = V_0\qquad (\rho=a)\qquad \qquad \phi=0\qquad (\rho=b)$

Suponiendo una solución dependiente sólo de $\rho$ (razonable, por ser el cable de gran longitud y poder despreciarse los efectos de borde), la ecuación de Laplace se reduce a

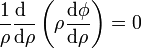
$\frac{1}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left(\rho\frac{\mathrm{d}\phi}{\mathrm{d}\rho}\right)=0$

con solución

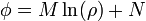
$\phi = M \ln(\rho) + N\,$

Imponiendo las condiciones de contorno

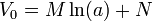
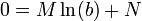
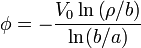
$V_0 =M \ln(a) + N\,$ $0 = M\ln(b) + N\,$ $\Rightarrow$ $\phi = -\frac{V_0\ln\left(\rho/b\right)}{\ln(b/a)}$

siendo el campo y la densidad de corriente en el material

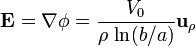
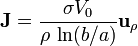
$\mathbf{E} = \nabla\phi= \frac{V_0}{\rho\,\ln(b/a)}\mathbf{u}_{\rho}$ $\mathbf{J} = \frac{\sigma V_0}{\rho\,\ln(b/a)}\mathbf{u}_{\rho}$

La corriente total que atraviesa el dieléctrico y la resistencia de éste las obtenemos calculando el flujo de $\mathbf{J}$ a través de una superficie que envuelva al cilindro interior

$I =\int \mathbf{J}{\cdot}\mathrm{d}\mathbf{S} = \int_0^h\!\! \mathrm{d}z\int_0^{2\pi}\!\!\!\! \mathrm{d}\varphi \rho\frac{\sigma V_0}{\rho\ln(b/a)} = \frac{2\pi h \sigma V_0}{\ln(b/a)}$

y de aquí resulta la resistencia

$R = \frac{\ln(b/a)}{2\pi h \sigma}$

Este cálculo es del todo análogo al de la obtención de la capacidad de un condensador coaxial, sin más que reemplazar $\varepsilon$ por $\sigma$.

Resistencia de un tubo

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Resistencia longitudinal

4 Resistencia transversal

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES