Una varilla y una carga

De Laplace

1 Enunciado

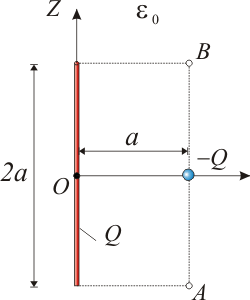
Una carga eléctrica Q está uniformemente distribuida a lo largo de un segmento rectilíneo de longitud 2a. A una distancia a del punto medio de dicho segmento y en dirección perpendicular a éste, se halla una carga puntual − Q.

1. Calcule el flujo del campo eléctrico a través de una superficie esférica de radio a / 2 centrada en el punto medio del segmento cargado (punto O).
2. Obtenga la fuerza que actúa sobre la carga puntual.
3. Calcule los momentos monopolar y dipolar de la distribución de carga descrita. Proponga expresiones aproximadas para el potencial y el campo eléctrico en puntos suficientemente alejados de la distribución.
4. ¿Qué trabajo habría que realizar para mover la carga puntual entre los puntos A al B? (ver figura)

2 Solución

2.1 Flujo del campo eléctrico a través de superficie esférica

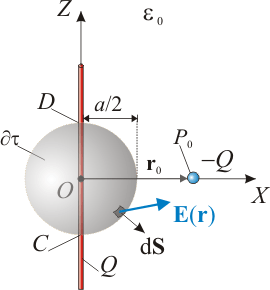
Tal como se indica en las figuras, adoptaremos un sistema de referencia cartesiano con origen en el centro de la varilla cargada, la cuál va a ser colineal con el eje 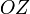. Además, consideraremos que la carga puntual 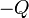se halla en el eje .

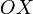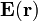En este apartado hay que calcular el flujo del campo eléctrico , a través de una superficie esférica : No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \Phi\big|_{\partial \tau}=\oint_{\partial \tau}\!\mathbf{E}\cdot \mathrm{d}\mathbf{S}\, \quad \mbox{con \qquad \mathbf{E}(\mathbf{r})=\mathbf{E}_\mathrm{car}(\mathbf{r})+\mathbf{E}_\mathrm{var}(\mathbf{r})

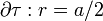Nótese que dicho campo debe ser el creado por toda la distribución de carga descrita; es decir, la carga puntual 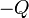colocada en el punto dado por el vector 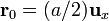, y la varilla de longitud 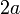cargada uniformemente con una cantidad de carga eléctrica, o lo que es lo mismo, con una densidad lineal de constante No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \ \lambda_e(z\')=\Delta Q/\Delta z/2a=\lambda_0

La expresión del campo eléctrico de una carga puntual es bien conocida, y el cálculo del campo eléctrico creado por un segmento con densidad lineal de carga constante puede verse en el ejercicio Campo eléctrico de un segmento cargado