Energía en un condensador con y sin dieléctrico
De Laplace
Contenido |
1 Enunciado
El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 3 mm está vacío.
Entre las placas se establece una diferencia de potencial de 20 V
- ¿Cuánto vale la energía almacenada en el sistema?
- Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (
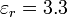) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
- Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?
2 Energía inicial
Inicialmente tenemos un condensador plano en vacío cuya capacidad es
que, cuando se encuentra a una diferencia de potencial V0 almacena una energía
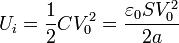
Para este sistema concreto los valores de la capacidad y la energía son
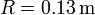a=0.003\,\mathrm{m}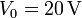 
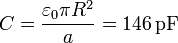
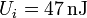
La carga almacenada en cada una de sus placas es
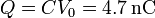
3 Energía final a carga constante
En el estado final, el sistema es uno formado por dos capas de dieléctrico, cuya capacidad equivale a la de dos condensadores puestos en serie.
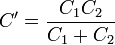
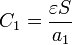
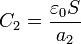
Nótese que no tenemos que especificar si la lámina de dieléctrico se encuentra adosada a una de las placas, a la otra, o no toca ninguna de las dos. Con que esté situada paralelamente a los electrodos es suficiente para obtener el resultado anterior.
En este caso concreto
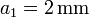
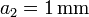
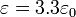
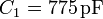
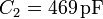
La capacidad del condensador aumenta en un 86% al introducir el dieléctrico, como consecuencia de su mayor permitividad.
En este apartado estamos suponiendo que las placas están aisladas, por lo que lo que se mantiene constante es la carga. La consecuencia del aumento en la capacidad es la reducción en la diferencia de potencial entre las placas
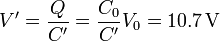
y, por tanto, de la energía almacenada, en la misma proporción
U_f = \frac{1}{2}QV'=\frac{1}{2}Q\left(\frac{C_0}{C'}V_0\right)=\frac{C_0}{C'}U_i=
