Corteza polarizada radialmente

De Laplace

Revisión a fecha de 13:04 10 jun 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Densidades de carga
3 Campo y desplazamiento
- 3.1 Partiendo de D
- 3.2 Partiendo de E
4 Potencial eléctrico

1 Enunciado

Una corteza esférica de radio interior

a

y exterior

b

está hecha de dieléctrico polarizado según la ley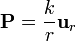 $\mathbf{P} = \frac{k}{r}\mathbf{u}_{r}$

No hay más cargas en el sistema

Calcule las densidades de carga de polarización en el sistema. ¿Cuánto vale la carga total de polarización?
Halle los campos $\mathbf{D}$ y $\mathbf{E}$ en todo el espacio.
Determine el valor del potencial eléctrico en todo el espacio.

2 Densidades de carga

En este problema no estamos considerando un material lineal con una permitividad dada, sino un dieléctrico en el que existe una cierta polarización conocida.

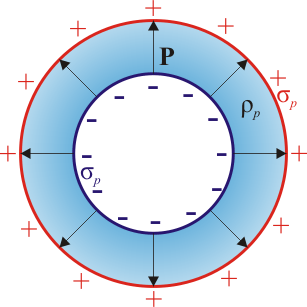
Las cargas de polarización equivalentes a la distribución de dipolos pueden ser superficiales o volumétricas. Las de volumen se encontrarían en la propia corona ( $a < r < b$ ) mientras que las superficiales estarían en las dos caras de este volumen ( $r = a$ y $r = b$ ).

La densidad volumétrica de cargas de polarización la hallamos empleando coordenadas esféricas y aplicando que la polarización es puramente radial.

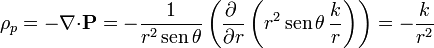
$\rho_p = -\nabla{\cdot}\mathbf{P} = -\frac{1}{r^2\,\mathrm{sen}\,\theta}\left(\frac{\partial{}\ }{\partial{}r}\left(r^2\,\mathrm{sen}\,\theta\,\frac{k}{r}\right)\right)= -\frac{k}{r^2}$

en $a < r < b$ y es nula en el resto del espacio.

Las densidades superficiales se calculan a partir del salto en la polarización. Para la cara exterior tenemos $\left.\sigma_p\right|_{r=b} = -\mathbf{n}{\cdot}[\mathbf{P}]= -\mathbf{u}_{r}{\cdot}\left(0-\frac{k}{b}\mathbf{u}_{r}\right) = \frac{k}{b}$

Obsérvese que se debe sustituir la coordenada $r$ por su valor en la cara exterior.

Para la cara interior, considerando la normal hacia adentro, tenemos

$\left.\sigma_p\right|_{r=a} = -\mathbf{n}{\cdot}[\mathbf{P}]= -(-\mathbf{u}_{r}){\cdot}\left(0-\frac{k}{a}\mathbf{u}_{r}\right) = -\frac{k}{a}$

Si $k$ es positivo, tenemos que la carga superficial interior es negativa, mientras que la exterior es positiva, como corresponde al hecho de que los dipolos apuntan hacia afuera.

La carga total de polarización será la suma de la de volumen más la de superficie

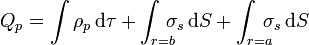
$Q_p = \int\rho_p\,\mathrm{d}\tau + \int_{r=b} \!\!\!\!\sigma_s \,\mathrm{d}S +\int_{r=a}\!\!\!\! \sigma_s \,\mathrm{d}S$

La carga total de volumen vale

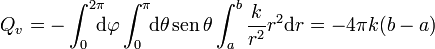
$Q_v = -\int_0^{2\pi}\!\!\!\! \mathrm{d}\varphi\int_0^\pi \!\! \mathrm{d}\theta\,\mathrm{sen}\,\theta\int_a^b \frac{k}{r^2} r^2 \mathrm{d}r = -4\pi k(b-a)$

Y las de superficie, al ser uniformes en cada cara

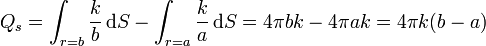
$Q_s = \int_{r=b} \frac{k}{b} \,\mathrm{d}S -\int_{r=a} \frac{k}{a}\,\mathrm{d}S = 4\pi b k -4\pi a k = 4\pi k(b-a)$

La carga total es nula, como debe ocurrir necesariamente

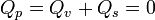
$Q_p = Q_v + Q_s = 0\,$

Esta anulación ocurre siempre, pues al estar el material formado por dipolos sin carga neta, la suma de todos los dipolos nunca puede dar una carga distinta de cero.

3 Campo y desplazamiento

3.1 Partiendo de D

La forma más sencilla de determinar el campo eléctrico es partiendo del vector desplazamiento.

Por la simetría del sistema, el desplazamiento eléctrico debe ser un campo central

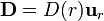
$\mathbf{D} = D(r)\mathbf{u}_{r}\,$

lo que implica que es necesariamente irrotacional

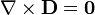
$\nabla\times\mathbf{D} = \mathbf{0}$ $\mathbf{n}\times[\mathbf{D}]=\mathbf{0}$

Por otro lado, al no haber cargas libres en el sistema, se cumple

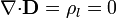
$\nabla{\cdot}\mathbf{D} = \rho_l = 0$ $\mathbf{n}{\cdot}[\mathbf{D}] = 0$

Por tanto, $\mathbf{D}$ carece tanto de fuentes escalares como vectoriales, y además se anula en el infinito. Ello implica que $\mathbf{D}$ es idénticamente nulo en todo el espacio

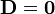
$\mathbf{D} = \mathbf{0}$

Una vez que tenemos esto, el cálculo del campo eléctrico es inmediato

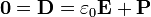
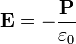
$\mathbf{0} = \mathbf{D} = \varepsilon_0 \mathbf{E} + \mathbf{P}$ $\Rightarrow$ $\mathbf{E} = -\frac{\mathbf{P}}{\varepsilon_0}$

Sustituyendo el valor de la polarización queda

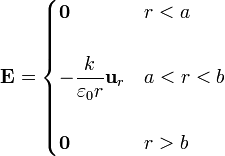
$\mathbf{E} = \begin{cases}\mathbf{0} & r<a\\ & \\ -\displaystyle\frac{k}{\varepsilon_0 r}\mathbf{u}_{r} & a<r<b\\ \\\mathbf{0} & r>b\end{cases}$

3.2 Partiendo de E

Si el atajo anterior no se conoce, el campo eléctrico también puede determinarse de forma directa por aplicación de la ley de Gauss.

Por la simetría tenemos que $\mathbf{E}$ es un campo central

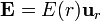
$\mathbf{E} = E(r)\mathbf{u}_{r}\,$

lo que nos simplifica el cálculo del flujo a través de una superficie esférica cualquiera con centro el de la corteza esférica

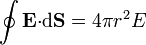
$\oint \mathbf{E}{\cdot}\mathrm{d}\mathbf{S} = 4\pi r^2 E$

Este flujo debe ser igual a la carga total (libre más de polarización) contenida en su interior. Tenemos tres casos

3.2.1 Interior del hueco

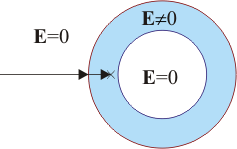
En el interior del hueco no hay ninguna carga por lo que

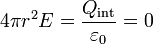
$4\pi r^2 E = \frac{Q_\mathrm{int}}{\varepsilon_0} = 0$ $\Rightarrow$ $\mathbf{E} = \mathbf{0} \qquad (r<a)$

3.2.2 Corona esférica

Si estamos en el propio material dieléctrico, la carga contenida es doble: por un lado la almacenada en la superficie interior y por otro la porción de carga de volumen contenida por la esfera de radio $r$ . La carga interior valdrá

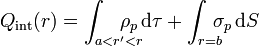
$Q_\mathrm{int}(r) = \int_{a<r'<r} \!\!\!\!\!\!\!\! \rho_p \,\mathrm{d}\tau + \int_{r=b} \!\!\!\! \sigma_p\,\mathrm{d}S$

Sustituyendo e integrando como el apartado anterior resulta

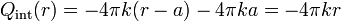
$Q_\mathrm{int}(r) = -4\pi k (r-a) - 4\pi k a = -4\pi k r\,$

de donde

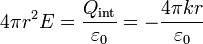
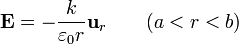
$4\pi r^2 E = \frac{Q_\mathrm{int}}{\varepsilon_0} = -\frac{4\pi k r}{\varepsilon_0}$ $\Rightarrow$ $\mathbf{E} = -\frac{k}{\varepsilon_0 r}\mathbf{u}_r\qquad (a<r<b)$

Este campo va dirigido hacia adentro, esto es, desde las cargas de polarización positivas hacia las negativas. Nótese que no se verifica 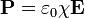$\mathbf{P} = \varepsilon_0 \chi \mathbf{E}$ , ya que si ese fuera el caso, $\mathbf{E}$ y $\mathbf{P}$ $ deberían ir en el mismo sentido.

3.2.3 Exterior de la esfera

Por último tenemos los puntos exteriores a la corteza. Para estos, la carga interior es la carga total de polarización, que es nula, según vimos antes. Por tanto

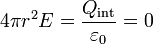
$4\pi r^2 E = \frac{Q_\mathrm{int}}{\varepsilon_0} = 0$ $\Rightarrow$ $\mathbf{E} = \mathbf{0} \qquad (r>b)$

llegándose finalmente al resultado que ya conocemos.

Una vez que tenemos el campo eléctrico, hallamos el vector desplazamiento

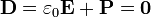
$\mathbf{D}=\varepsilon_0\mathbf{E}+\mathbf{P}=\mathbf{0}$

4 Potencial eléctrico

Una vez que tenemos el campo eléctrico, la determinación del potencial es inmediata, a partir de la integral

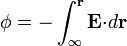
$\phi = -\int_\infty^\mathbf{r} \mathbf{E}{\cdot}d\mathbf{r}$

Al ser 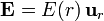$\mathbf{E}=E(r)\,\mathbf{u}_{r}$ esta integral se reduce a una en $r$ , resultando un potencial central $φ = φ(r)$ .

De nuevo tenemos tres casos según estemos en el exterior de la corteza, en ella misma, o en su interior.

4.1 Exterior de la esfera

En el exterior el campo es nulo en todos los puntos, por lo que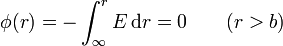 $\phi(r) = -\int_\infty^r E\,\mathrm{d}r = 0 \qquad (r>b)$

4.2 Corona esférica

En la corteza, la integral desde el infinito se descompone en dos tramos, uno hasta la superficie exterior, y otro desde ahí hasta el punto del interior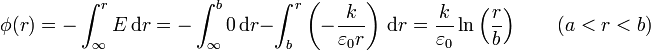 $\phi(r) = -\int_\infty^r E\,\mathrm{d}r = -\int_\infty^b 0\,\mathrm{d}r -\int_b^r \left(-\frac{k}{\varepsilon_0 r}\right)\,\mathrm{d}r =\frac{k}{\varepsilon_0}\ln\left(\frac{r}{b}\right)\qquad (a<r<b)$

4.3 Hueco interior

Por último, en el interior del hueco, el campo es nulo de nuevo. No así el potencial, que será constante. El valor de la constante lo obtenemos integrando otra vez desde el infinito dividiendo en esta ocasión la integral en tres tramos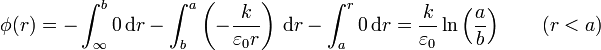 $\phi(r) = -\int_\infty^b 0\,\mathrm{d}r -\int_b^a \left(-\frac{k}{\varepsilon_0 r}\right)\,\mathrm{d}r -\int_a^r 0\,\mathrm{d}r = \frac{k}{\varepsilon_0}\ln\left(\frac{a}{b}\right) \qquad (r<a)$

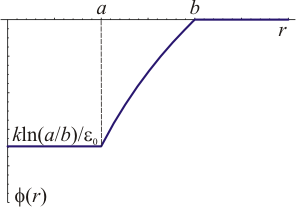
Reuniendo los tres resultados obtenemos la expresión para el potencial

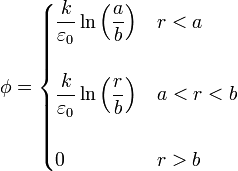
$\phi=\begin{cases}\displaystyle\frac{k}{\varepsilon_0}\ln\left(\displaystyle\frac{a}{b}\right) & r<a\\ & \\ \displaystyle\frac{k}{\varepsilon_0}\ln\left(\displaystyle\frac{r}{b}\right) & a<r<b \\ & \\ 0 & r>b\end{cases}$

El potencial pasa de una constante exterior a una interior, variando sólo a lo largo de la corona esférica.

Imagen:potencial-corteza-dielectrica.png

Corteza polarizada radialmente

De Laplace

Contenido

1 Enunciado

2 Densidades de carga

3 Campo y desplazamiento

3.1 Partiendo de D

3.2 Partiendo de E

3.2.1 Interior del hueco

3.2.2 Corona esférica

3.2.3 Exterior de la esfera

4 Potencial eléctrico

4.1 Exterior de la esfera

4.2 Corona esférica

4.3 Hueco interior

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES