Corteza polarizada radialmente

De Laplace

Revisión a fecha de 12:16 10 jun 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Densidades de carga
3 Campo y desplazamiento
4 Potencial eléctrico

1 Enunciado

Una corteza esférica de radio interior $a$ y exterior $b$ está hecha de dieléctrico polarizado según la ley

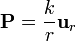
$\mathbf{P} = \frac{k}{r}\mathbf{u}_{r}$

No hay más cargas en el sistema

Calcule las densidades de carga de polarización en el sistema. ¿Cuánto vale la carga total de polarización?
Halle los campos $\mathbf{D}$ y $\mathbf{E}$ en todo el espacio.
Determine el valor del potencial eléctrico en todo el espacio.

2 Densidades de carga

En este problema no estamos considerando un material lineal con una permitividad dada, sino un dieléctrico en el que existe una cierta polarización conocida.

Las cargas de polarización equivalentes a la distribución de dipolos pueden ser superficiales o volumétricas. Las de volumen se encontrarían en la propia corona ($a<r<b$) mientras que las superficiales estarían en las dos caras de este volumen ( $r = a$ y $r = b$ ).

La densidad volumétrica de cargas de polarización la hallamos empleando coordenadas esféricas y aplicando que la polarización es puramente radial.

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \rho_p = -\nabla{\cdot}\mathbf{P} = -\frac{1}{r^2\,\mathrm{\sen}\,\theta}\left(\frac{\partial{}\ }{\partial{}r}\left(r^2\,\mathrm{\sen}\,\theta\,\frac{k}{r}\right)\right)= -\frac{k}{r^2}

en $a < r < b$ y es nula en el resto del espacio.

Las densidades superficiales se calculan a partir del salto en la polarización. Para la cara exterior tenemos

$\left.\sigma_p\right|_{r=b} = -\mathbf{n}{\cdot}[\mathbf{P}]= -\mathbf{u}_{r}{\cdot}\left(0-\frac{k}{b}\mathbf{u}_{r}\right) = \frac{k}{b}$

Obsérvese que se debe sustituir la coordenada $r$ por su valor en la cara exterior.

Para la cara interior, considerando la normal hacia adentro, tenemos

$\left.\sigma_p\right|_{r=a} = -\mathbf{n}{\cdot}[\mathbf{P}]= -(-\mathbf{u}_{r}){\cdot}\left(0-\frac{k}{a}\mathbf{u}_{r}\right) = -\frac{k}{a}$

Si $k$ es positivo, tenemos que la carga superficial interior es negativa, mientras que la exterior es positiva, como corresponde al hecho de que los dipolos apuntan hacia afuera.

La carga total de polarización será la suma de la de volumen más la de superficie

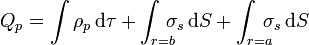
$Q_p = \int\rho_p\,\mathrm{d}\tau + \int_{r=b} \!\!\!\!\sigma_s \,\mathrm{d}S +\int_{r=a}\!\!\!\! \sigma_s \,\mathrm{d}S$

La carga total de volumen vale

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): Q_v = -\int_0^{2\pi}\!\!\!\! \mathrm{d}\varphi\int_0^\pi \!\! \mathrm{d}\theta\,\sen\theta\int_a^b \frac{k}{r^2} r^2 \mathrm{d}r = -4\pi k(b-a)

Y las de superficie, al ser uniformes en cada cara

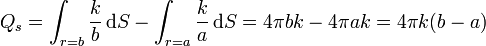
$Q_s = \int_{r=b} \frac{k}{b} \,\mathrm{d}S -\int_{r=a} \frac{k}{a}\,\mathrm{d}S = 4\pi b k -4\pi a k = 4\pi k(b-a)$

La carga total es nula, como debe ocurrir necesariamente

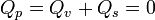
$Q_p = Q_v + Q_s = 0\,$

Esta anulación ocurre siempre, pues al estar el material formado por dipolos sin carga neta, la suma de todos los dipolos nunca puede dar una carga distinta de cero.

3 Campo y desplazamiento

4 Potencial eléctrico

Corteza polarizada radialmente

De Laplace

Contenido

1 Enunciado

2 Densidades de carga

3 Campo y desplazamiento

4 Potencial eléctrico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES