Dieléctrico lineal
De Laplace
Contenido |
1 Introducción. Relaciones constitutivas
Los medios dieléctricos se caracterizan por la presencia de dipolos, que contribuyen al campo eléctrico total. Estos dipolos se pueden modelar macroscópicamente mediante su densidad, la polarización 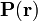 .
.
Cuando la polarización es conocida, puede determinarse el campo eléctrico que produce, bien por integración directa, bien sustituyendo la polarización por densidades de carga equivalentes y aplicando las técnicas de cálculo de campos producidos por cargas eléctrica.
Sin embargo, en la mayoría de las situaciones la polarización no es conocida a priori, ya que la aparición de dipolos se debe usualmente a la propia presencia del campo eléctrico. Por tanto, la polarización es tanto causa como efecto del campo eléctrico. Para hallar  debemos conocer
debemos conocer  y para conocer
y para conocer  debemos hallar
debemos hallar  .
.
Podemos escapar de este círculo vicioso estableciendo empíricamente (o mediante un modelo acertado) una relación constritutiva

que establezca cuánto vale la polarización para un cierto valor del campo total 8que incluye al de la propia polarización). Sustituyendo esta relación en las ecuaciones de la electrostática reducimos el sistema de ecuaciones a uno en el que aparece exclusivamente el campo eléctrico y que podrá ser resuelto con mayor o menor dificultad.
Esta relación constitutiva será dependiente de cada material concreto, y de sus propiedades fisicoquímicas. Podrá ser no-lineal (dependiente como una cierta potencia del campo, o mediante una función aun más complicada), incluir efectos de dispersión, de histéresis, etc.
Por ello, no es posible dar una solución general para la determinación del campo eléctrico en medios dieléctricos.
2 Definición
No obstante la posible generalidad de las relaciones constitutivas, se encuentra empíricamente que en la mayoría de los medios dieléctricos, cuando se aplica un campo electrostático de amplitud pequeña o moderada, la polarización resultante es simplemente proporcional al campo eléctrico
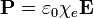
A un material que verifica esta relación constitutiva se le denomina dieléctrico lineal. La cantidad adimensional χe es la denominada susceptibilidad eléctrica.
La relación constitutiva de los dieléctricos lineales nos dice que en ausencia de campo eléctrico la polarización es nula y que a medida que va aumentando el campo aplicado, aumenta la polarización en forma proporcional.
2.1 Medio anisótropo
En su forma más general, la susceptibilidad es un tensor, representable por una matriz, de forma que la relación constitutiva se escribirá
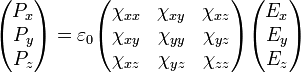
Este tensor es simétrico, por lo que siempre se pueden elegir unos ejes ortogonales (denominados ejes principales), tales que la relación se convierta en una diagonal
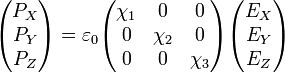
Un material en el que se verifica esta forma de la relación lineal se denomina medio anisótropo, ya que en ellos, para un campo aplicado de la misma magnitud, el valor de la polarización depende de la dirección en que se aplique. En un medio anisótropo, además, la dirección de la polarización no será en general paralela al campo eléctrico, salvo que éste se aplique según uno de los ejes principales.





