Inducción mutua de dos solenoides cuadrados

De Laplace

Contenido 1 Enunciado 2 Coeficientes 2.1 De autoinducción 2.2 De inducción mutua 2.3 Empleando la energía magnética 3 Asociaciones

1 Enunciado

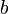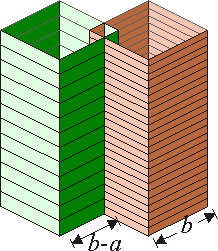
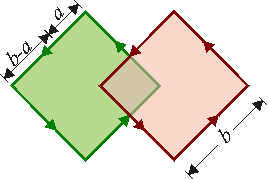
Se tienen dos solenoides de sección cuadrada de lado de un hilo ideal sin resistencia. La longitud de ambos solenoides es (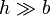) y el número de vueltas es N₁ = N y N₂ = 2N, respectivamente. Ambos solenoides se colocan de forma que intersecan en una sección cuadrada de lado a, tal como muestra la figura.

1. Halle los coeficientes de autoinducción, de inducción mutua y de acoplamiento.
2. Sin mover los solenoides de sitio, el sistema se conecta a un circuito. Para el caso a = b / 3, halle todas las posibles autoinducciones equivalentes que se pueden obtener con este sistema, teniendo en cuenta que los solenoides pueden conectarse entre sí, cortocircuitarse con un hilo ideal o dejarse en circuito abierto.

2 Coeficientes

2.1 De autoinducción

Si despreciamos los efectos de borde, cada uno de los solenoides produce un campo magnético que es constante en el interior y nulo en el exterior. El campo en el interior es el mismo que produciría una corriente superficial de módulo K = NI / h, esto es, la corriente total partida por la longitud. El campo resultante es

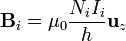
donde N_i es el número de espiras de un solenoide e I_i la corriente que circula por él.

Para hallar el coeficiente de autoinducción L₁₁ debemos hallar el flujo en el primer solenoide del campo magnético producido por él mismo. Este flujo se calcula a través de N₁ espiras cuadradas y el campo es constante en cada una por lo que el flujo vale

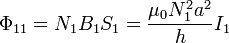
y el coeficiente de autoinducción correspondiente será

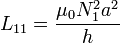
Igualmente se calcula el coeficiente L₂₂

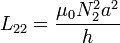
2.2 De inducción mutua

Para hallar el coeficiente de inducción mutua $L_{12}=L_{21}$ hay que calcular el flujo en el solenoide $1$ del campo producido por el solenoide $2$. Este flujo sólo es distinto de cero en el cuadrado de intersección, cuyo lado llamaremos $b$. Este flujo vale \[ \Phi_{12}=N_1 B_2 b^2=\frac{\mu_0N_1N_2 b^2}{h}I_2 \] y de aquí \[ L_{12}=L_{21}=\frac{\mu_0N_1N_2b^2}{h} \]

El valor de $b$ se relaciona con $a$ y con $x$ por la expresión \[ b=a-\frac{x}{\sqrt{2}} \] y \[ L_{12}=L_{21}=\frac{\mu_0N_1N_2}{h}\left(a-\frac{x}{\sqrt{2}}\right)^2 \]

2.3 Empleando la energía magnética

Si este cálculo se hace por energías debemos identificar las dos expresiones para la energía \[ W=\frac{1}{2\mu_0}\int B^2\,d\tau= \frac{1}{2}\left(L_{11}I_1^2+2L_{12}I_1I_2+L_{22}I_2^2\right) \] El campo magnético ya lo conocemos y vale $B_1$ en una zona de altura $h$ y sección $a^2-b^2$, $B_2$ en otra región de las mismas dimensiones y $B_1+B_2$ en la intersección, de longitud $h$ y sección $b^2$. Puesto que $B$ es constante en cada región, puede sacarse de la integral y el resultado es \ba W & = & \frac{1}{2\mu_0}\left(B_1^2(a^2-b^2)h+B_2^2(a^2-b^2)h+ (B_1+B_2)^2b^2h\right)= \\ & = & \frac{1}{2}\left(\frac{\mu_0N_1^2a^2}{h}I_1^2+ \frac{\mu_0N_2^2a^2}{h}I_2^2+ 2\frac{\mu_0N_1N_2b^2}{h}I_1I_2\right) \ea de donde \ba L_{11} & = & \frac{\mu_0N_1^2 a^2}{h} \qquad L_{22}=\frac{\mu_0N_2^2 a^2}{h} \\ L_{12} & = & L_{21}=\frac{\mu_0N_1N_2}{h} \left(a-\frac{x}{\sqrt{2}}\right)^2 \ea

3 Asociaciones