Fuerzas sobre cargas puntuales en un triángulo equilátero

De Laplace

Revisión a fecha de 18:26 29 may 2009; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

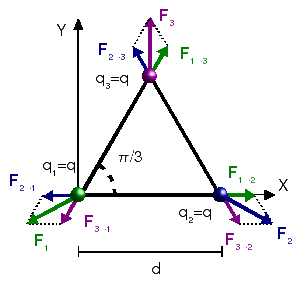
Se tiene un triángulo equilátero de lado d = 1 cm. En cada uno de sus vértices hay una carga puntual. Determine la fuerza sobre cada carga cuando

q1 = q2 = q3 = 1 μC.
q1 = q2 = q3 = −1 μC.
q1 = q2 = 1 μC, q3 = −1 μC.
q1 = q2 = 1 μC, q3 = −2 μC.

2 Solución

La Ley de Coulomb nos dice que fuerzas se ejercen dos cargas entre sí, mientras que el Principio de Superposición afirma que dado un conjunto de cargas, la fuerza que éstas ejercen sobre una carga puntual es igual a la suma de las fuerzas que ejerce sobre esa carga cada una de ellas Hay que recordar que la fuerza es una magnitud vectorial, y por tanto la fuerza total es una suma vectorial

2.1 Caso 1

En este caso las cargas son

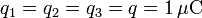
$q_1=q_2=q_3=q=1\,\mathrm{\mu C}$

Veamos la fuerza sobre la carga $q 3$ . Aplicando la ley de Coulomb y el principio de superposición tenemos

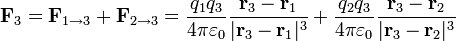
$\mathbf{F}_3 = \mathbf{F}_{1\to3}+\mathbf{F}_{2\to3}= \frac{q_1q_3}{4\pi\varepsilon_0}\frac{\mathbf{r}_3-\mathbf{r}_1}{|\mathbf{r}_3-\mathbf{r}_1|^3}+ \frac{q_2q_3}{4\pi\varepsilon_0}\frac{\mathbf{r}_3-\mathbf{r}_2}{|\mathbf{r}_3-\mathbf{r}_2|^3}$

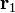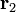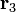Aquí, $\mathbf{r}_1$ , $\mathbf{r}_2$ , $\mathbf{r}_3$ son los vectores de posición de las cargas respecto a un sistema de referencia arbitrario.

Escogemos el origen de coordenadas coincidiendo con la carga $q 1$ , el eje $X$ a lo largo de la línea que une las cargas $q 1$ y $q 2$ , y el plano $O X Y$ de modo que coincida con el plano del triángulo (ver figura). Con este sistema los vectores de posición de las cargas son

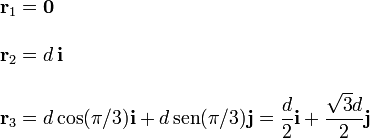
$\begin{array}{l} \mathbf{r}_1=\mathbf{0}\\ \\ \mathbf{r}_2=d\,\mathbf{i}\\ \\ \mathbf{r}_3=d\cos(\pi/3)\mathbf{i}+d\,\mathrm{sen}(\pi/3)\mathbf{j}= \displaystyle \frac{d}{2}\mathbf{i}+\frac{\sqrt{3}d}{2}\mathbf{j} \end{array}$

Al ser un triángulo equilátero los tres ángulos interiores son iguales a $π / 3$ . Los vectores que aparecen en la expresión de la fuerza son

$\begin{array}{lcl} \displaystyle \mathbf{r}_3-\mathbf{r}_1=\frac{d}{2}\mathbf{i}+\frac{\sqrt{3}d}{2}\mathbf{j}&\Longrightarrow&|\mathbf{r}_3-\mathbf{r}_1|=d \\ && \\ \displaystyle \mathbf{r}_3-\mathbf{r}_2=-\frac{d}{2}\mathbf{i}+\frac{\sqrt{3}d}{2}\mathbf{j}&\Longrightarrow&|\mathbf{r}_3-\mathbf{r}_2|=d \end{array}$

Teniendo en cuenta que las tres cargas son iguales la fuerza sobre la carga $q 3$ es

$\mathbf{F}_3=\frac{q^2}{4\pi\varepsilon_0d^2} \left[ \left(\frac{1}{2}\mathbf{i}+\frac{\sqrt{3}}{2}\mathbf{j}\right)+ \left(-\frac{1}{2}\mathbf{i}+\frac{\sqrt{3}}{2}\mathbf{j}\right) \right]=\frac{\sqrt{3}q^2}{4\pi\varepsilon_0d^2}\mathbf{j}$

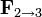La fuerza resultante sobre la carga $q 3$ está dirigida en la dirección del eje $Y$ , es decir, en la dirección de la mediatriz del lado opuesto a la carga $q 3$ . Esta dirección es resultado de la simetría de las fuerzas que actúan sobre la carga. Como se observa en la figura las fuerzas $\mathbf{F}_{1\to3}$ y $\mathbf{F}_{2\to3}$ son iguales en módulo, pues las cargas tienen el mismo valor y las distancias entre las cargas son iguales. Pero las direcciones son diferentes, de un modo tal que se cancelan las componentes paralelas al eje $X$ . Con los valores numéricos del enunciado el módulo de esta fuerza vale

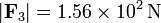
$|\mathbf{F}_3|=1.56\times10^2\,\mathrm{N}$

Si suponemos que la masa de la carga es $m =$ 10 g, la aceleración que le conferiría esta fuerza sería

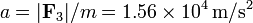
$a=|\mathbf{F}_3|/m = 1.56\times10^4\,\mathrm{m/s^2}$

Podemos usar el mismo procedimiento para calcular las fuerzas sobre las otras cargas, aunque si observamos el dibujo podemos saber como van a ser estas fuerzas. Como las tres cargas son iguales y el triángulo es equilátero, podemos girar el sistema un ángulo $π / 3$ y todo debe quedar igual. Por tanto, para cada carga la fuerza estará dirigida en la dirección de la mediatriz del lado opuesto del triángulo, repulsiva, y con módulo igual al que hemos calculado antes.

Fuerzas sobre cargas puntuales en un triángulo equilátero

De Laplace

1 Enunciado

2 Solución

2.1 Caso 1

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES