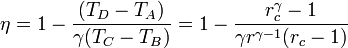Ciclo Diesel
De Laplace
Contenido |
1 Enunciado
Un motor diésel puede modelarse con el ciclo ideal formado por seis pasos reversibles, según se indica en la figura. Pruebe que el rendimiento de este ciclo viene dado por la expresión
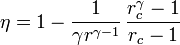
siendo r = VA / VB la razón de compresión y rc = VC / VB la relación de combustión. El método para obtener este resultado es análogo al empleado para el ciclo Otto. Compare los rendimientos del ciclo de Otto y el diésel. ¿Cuáles son las ventajas e inconvenientes respectivos?
2 Rendimiento en función de las temperaturas
Un ciclo diésel contiene dos proceso adiabáticos, A→B y C→D, en los que no se intercambia calor. De los otros dos, en el calentamiento a presión constante B→C, el gas recibe una cantidad de calor | Qc | del exterior igual a
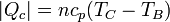
En el enfriamiento a volumen constante D→A el sistema cede una cantidad de calor al ambiente
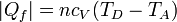
El rendimiento del ciclo será entonces
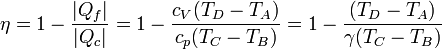
con γ = cp / cV la proporción entre las capacidades caloríficas.
3 Rendimiento en función de los volúmenes
La expresión anterior requiere conocer las cuatro temperaturas de los vértices del ciclo. Puede simplificarse teniendo en cuenta las características de cada uno de los procesos que lo componen.
Así tenemos, para la compresión adiabática A→B
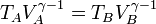
que, teniendo en cuenta la relación de compresión, podemos reescribir como
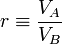

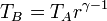
Para la expansión a presión constante, aplicando la ecuación de estado de los gases ideales
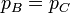

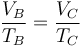
Introduciendo ahora la relación rc = VC / VB obtenemos
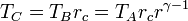
Por último, para la temperatura en D aplicamos de nuevo la ley de Poisson y el que el enfriamiento es a volumen constante:
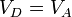
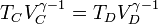

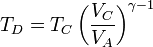
Multiplicando y dividiendo por VB y aplicando el valor de la temperatura en C
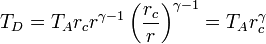
Combinado estos resultados nos queda
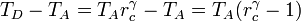
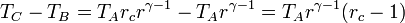
Sustituyendo esto en la expresión del rendimiento obtenemos finalmente