Barra que se mueve en un campo uniforme
De Laplace
Contenido |
1 Enunciado
Una barra metálica de longitud se mueve en el interior de un campo magnético uniforme
se mueve en el interior de un campo magnético uniforme  (
(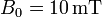 ) con velocidad constante
) con velocidad constante  , siendo
, siendo  perpendicular tanto al eje de la varilla como al campo magnético y de módulo
perpendicular tanto al eje de la varilla como al campo magnético y de módulo 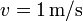 .
.
- Calcule la fuerza magnética sobre una carga
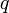 de la varilla. ¿Hacia donde se mueven las cargas positivas y negativas de la varilla?
de la varilla. ¿Hacia donde se mueven las cargas positivas y negativas de la varilla?
- La separación de carga alcanza el equilibrio cuando la fuerza eléctrica debido a dicha separación compensa exactamente la fuerza magnética. Usando esto, halle el campo eléctrico en el interior de la varilla.
- Calcule el voltaje entre los extremos de la varilla.
- Calcule la f.e.m. inducida, de acuerdo con la ley de Faraday, a lo largo de una curva formada por la varilla y un cierre por el exterior del campo magnético. Compruebe que coincide con el voltaje calculado en el apartado anterior.
2 Fuerza sobre una carga
Cada una de las cargas de la barra se mueve solidariamente con ésta, por lo que cada carga experimentará una fuerza magnética
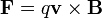
Si consideramos como eje X el definido por la velocidad y Z el definido por el campo, el eje Y será en la dirección de la varilla, con el signo positivo en la parte superior de la figura. La fuerza apunta en esta misma dirección
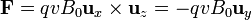
Las cargas positivas experimentan una fuerza hacia abajo mientras que las cargas negativas la sufrirán hacia arriba. El campo magnético, por tanto, separa las cargas de la barra. La fuerza magnética por unidad de carga actúa como un campo efectivo 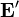 , de los presentes en los generadores.
, de los presentes en los generadores.
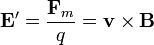
3 Campo eléctrico
La fuerza magnética separa las cargas eléctricas, pero nunca llega (ni de lejos) a producir una separación total. En el momento que se produce una acumulación de carga en los extremos de la barra aparece un campo eléctrico que va de las cargas positivas a las negativas y que tiende a reunirlas.
El proceso de acumulación se detiene cuando se alcanza el equilibrio y la fuerza eléctrica compensa exactamente a la magnética. En este momento
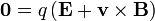

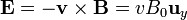
Este campo eléctrico, según los ejes que hemos tomado, irá del extremo inferior al superior.
4 Voltaje
La caída de tensión entre los dos extremos de la barra lo da la integral del campo eléctrico. Si tomamos como polo positivo P el superior y como negativo N el inferior, aunque sepamos que las cargas poseen signos opuestos a los polos que hemos tomado, nos resulta un voltaje
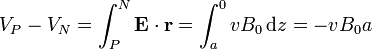
La razón de tomar este criterio de signos es para mantener la consistencia con el apartado siguiente.
5 Fuerza electromotriz
Para hallar la fuerza electromotriz debemos imaginarnos una curva cerrada, no necesariamente material, que pase por el interior de la barra del cátodo N al ánodo P y por fuera del ánodo al cátodo. La fuerza electromotriz a lo largo de esta curva es
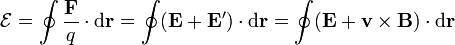
La integral del campo eléctrico a lo largo de la curva cerrada se anula, por ser \mathbf{E} irrotacional. La fuerza magnética sólo es no nula dentro de la barra, por lo que
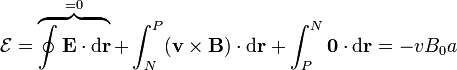
Este resultado necesariamente coincide con el anterior, ya que también lo podríamos haber obtenido observando que dentro de la barra la fuerza eléctrica anula a la magnética y por tanto
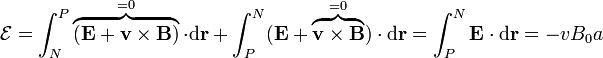
Nótese que para integrar el campo eléctrico es indiferente hacerlo por dentro de la barra que por fuera, por ser la integral independiente del camino.






