Producción de entropía en un frigorífico real

De Laplace

1 Enunciado

Para mantener su interior a 4°C en una habitación que se encuentra a 27 °C un refrigerador ha de extraer 360 kJ/min de su interior. Si la entrada de potencia requerida por el refrigerador es 2 kW, determine:

1. Eficiencia del refrigerador. Compárela con la eficiencia de un refrigerador ideal (reversible) que trabaje entre los mismos focos térmicos.
2. Potencia extra que consume este frigorífico respecto a uno ideal que extraiga la misma energía de su interior.
3. Entropía generada por segundo en el universo por la operación del frigorífico real.

2 Eficiencia del refrigerador

La eficiencia de un refrigerador se expresa habitualmente en términos del coeficiente de operación (COP), denotado por COP_R. También se utiliza a veces la letra η. USaremos esta última notación en este problema.

La eficiencia de un refrigerador es el calor extraído del foco frío dividido por el trabajo requerido para hacer funcionar el refrigerador. Por supuesto esta definición es igualmente válida cuando se emplea el calor extraido y el trabajo requerido por unidad de tiempo. Entonces para nuestro refrigerador tenemos:

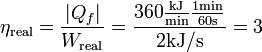
Esta eficiencia se encuentra dentro del rango de valores típicos del COP para refrigeradores reales.

Por otra parte, sabemos que para un refrigerador ideal la eficiencia es una función exclusivamente de las temperaturas del foco frío y del foco caliente:

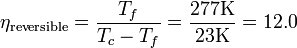
Es decir, que la eficiencia del refrigerador real es un 25% de la eficiencia teórica máxima que se podría alcanzar para un refrigerador trabajando entre esos focos térmicos. Esto es lo que suele denominarse eficiencia de la segunda ley ó eficiencia del segundo principio.

3 Potencia extra consumida

El trabajo extra puede calcularse como 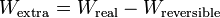y si asumimos que ambas máquinas absorben el mismo calor 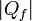del foco frío, podemos operar así:

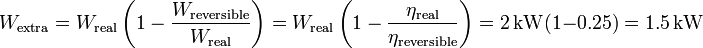
Es decir, que de los 2 kW empleados en hacer funcionar la máquina el 25% (0.5 kW) corresponden a la potencia que necesitaría una máquina reversible para obtener el mismo resultado y el resto (1.5 kW) es trabajo extra que ha de realizarse debido a las irreversibilidades del proceso real que sigue el refrigerador.

4 Entropía generada

Aunque el resultado del apartado anterior podría haberse obtenido de una forma directa a partir de las eficiencias calculadas en el primer apartado del problema, el análisis teórico realizado previamente nos ha permitido relacionar la disminución de eficiencia asociada a las irreversibilidades con el incremento de entropía total o del universo (sistema + entorno). A partir de esto es inmediato calcular el incremento de entropía total:

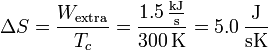
Nótese que al estar la energía expresada por unidad de tiempo (potencia) lo que obtenemos realmente es el incremento de entropía del universo por segundo (ritmo de generación de entropía).