Tiempo de un sonido para llegar al suelo

De Laplace

Revisión a fecha de 14:59 4 may 2009; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Cálculo aproximado
- 2.2 Cálculo exacto

1 Enunciado

La temperatura de la atmósfera en sus capas bajas decrece con la altura como

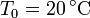
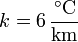
$T(^\circ\mathrm{C}) = T_0-kz\,$ $T_0 = 20\,^\circ\mathrm{C}$ $k = 6\,\frac{^\circ\mathrm{C}}{\mathrm{km}}$

Un avión rompe la barrera del sonido cuando se encuentra a 8 km de altura. ¿Cuánto tarda el estampido sónico en llegar al suelo?

2 Solución

2.1 Cálculo aproximado

Antes de realizar el cálculo exacto, que requiere hacer integrales, vamos a hacer una estimación del resultado, para ver si el efecto de la variación térmica es apreciable.

La temperatura en el camino del sonido varía desde 20 ºC al nivel del suelo hasta (20 − 6·8) ºC=-28 ºC a la altura del avión h = 8 km. La velocidad del sonido a estas dos alturas es

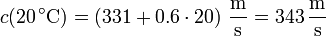
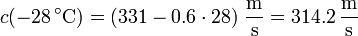
$c(20\,^\circ\mathrm{C}) = \left(331+0.6\cdot 20\right)\,\frac{\mathrm{m}}{\mathrm{s}}=343\,\frac{\mathrm{m}}{\mathrm{s}}$ $c(-28\,^\circ\mathrm{C}) = \left(331-0.6\cdot 28\right)\,\frac{\mathrm{m}}{\mathrm{s}}=314.2\,\frac{\mathrm{m}}{\mathrm{s}}$

El tiempo que tarda el estampido en llegar al suelo estará entre los correspondientes a estas dos velocidades

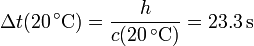
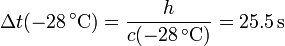
$\Delta t(20\,^\circ\mathrm{C}) = \frac{h}{c(20\,^\circ\mathrm{C})}=23.3\,\mathrm{s}$ $\Delta t(-28\,^\circ\mathrm{C}) = \frac{h}{c(-28\,^\circ\mathrm{C})}=25.5\,\mathrm{s}$

Vemos que los dos tiempos están próximos y que el error que cometemos al suponer que la temperatura es constante en todo el camino no supera el 10%.

2.2 Cálculo exacto

Veamos cómo sería el cálculo exacto. El sonido comienza su camino a 8 km de altura, a una temperatura de -28 ºC. A esta altura la velocidad del sonido es 314 m/s, según hemos visto. Cuando el sonido recorre una pequeña distancia vertical $d z$ , emplea un tiempo $d t$ y desciende a una zona de menor altura y mayor temperatura, en la que el sonido posee mayor velocidad. Con esta nueva velocidad recorre otra pequeña distancia, en la que empleará un tiempo diferente.

El tiempo necesario para recorrer una distancia vertical $d z$ a una velocidad $c$ será

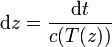
$\mathrm{d}z=\frac{\mathrm{d}t}{c(T(z))}$

El tiempo total en llegar hasta el suelo será la suma de los intervalos correspondientes a cada pequeña altura $d z$

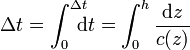
$\Delta t = \int_0^{\Delta t}\!\!\!\!\mathrm{d}t=\int_0^h \frac{\mathrm{d}z}{c(z)}$

La dependencia de la velocidad con la altura es una función lineal, ya que

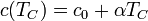
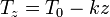
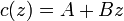
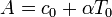
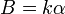
$c(T_C) = c_0 + \alpha T_C\,$ $T_z=T_0-k z\,$ $\Rightarrow$ $c(z) = A+Bz\,$ $A=c_0+\alpha T_0\,$ $B=k\alpha\,$

Llevando esto a la integral

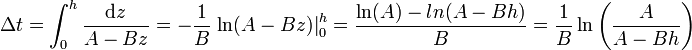
$\Delta t=\int_0^h\frac{\mathrm{d}z}{A-Bz} = -\frac{1}{B}\left.\ln(A-Bz)\right|_0^h = \frac{\ln(A)-ln(A-Bh)}{B}=\frac{1}{B}\ln\left(\frac{A}{A-Bh}\right)$

Pero $A$ y $A - B h$ son precisamente las velocidades a nivel del suelo y a una altura $h$ . Por ello, el intervalo puede escribirse como

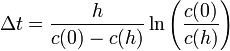
$\Delta t = \frac{h}{c(0)-c(h)}\ln\left(\frac{c(0)}{c(h)}\right)$

Sustituyendo los valores numéricos

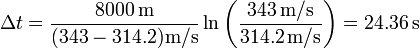
$\Delta t = \frac{8000\,\mathrm{m}}{(343-314.2)\mathrm{m}/\mathrm{s}}\ln\left(\frac{343\,\mathrm{m}/\mathrm{s}}{314.2\,\mathrm{m}/\mathrm{s}}\right)=24.36\,\mathrm{s}$

Vemos que, efectivamente el valor es intermedio entre los dos que calculamos antes. El error que habríamos cometido al suponer que la temperatura es la misma que a nivel del suelo sería

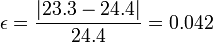
$\epsilon=\frac{|23.3-24.4|}{24.4}=0.042$

esto es, en torno al 5%, lo cual, teniendo en cuenta que el modelo que supone una variación estrictamente lineal de la temperatura con la altura es solo aproximado, representa un resultado perfectamente aceptable.

Tiempo de un sonido para llegar al suelo

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Cálculo aproximado

2.2 Cálculo exacto

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES