Conducción térmica en dos barras en contacto
De Laplace
Contenido[ocultar] |
1 Enunciado
Una barra de oro está en contacto térmico con otra de plata de la misma longitud y área. Uno de los extremos de esta barra compuesta se mantiene a una temperatura de 80oC, mientras que el extremo opuesto está a 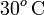 . Cuando la transferencia de energía alcance un estado estacionario, ¿cuál será la temperatura en la unión?
. Cuando la transferencia de energía alcance un estado estacionario, ¿cuál será la temperatura en la unión?
Datos: conductividad térmica del oro: 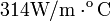 ;
conductividad térmica de la plata:
;
conductividad térmica de la plata: 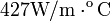
2 Solución
2.1 Barra homogénea
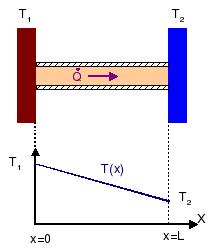
Examinemos primero el caso más sencillo de una barra homogénea de longitud L y conductividad térmica k sometida a temperaturas T1 y T2, con T1 > T2.
En la situación estacionaria, la potencia de energía térmica transferida desde el foco caliente al frío debe ser la misma en todos los puntos de la barra. Si no fuera así, la energía recibida en un punto de la barra desde un lado sería mayor que la que sale hacia el otro, y la temperatura variaría en el tiempo. La potencia es
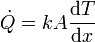
donde k es la conductividad del material y A el área de la superficie a través de la que se transmite la energía. Nuestro objetivo es encontrar la función T(x) que describe la distribución de temperaturas entre los focos a T1 y T2. Como la potencia 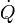 debe ser la misma en cada punto de la barra, debe cumplirse
debe ser la misma en cada punto de la barra, debe cumplirse
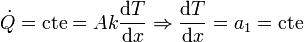
Es decir,
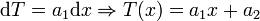
Las constantes a1 y a2 se determinan imponiendo que las temperaturas en los extremos de la barra deben ser T1 y T2.
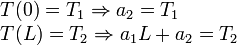
De este modo la distribución de temperaturas en la barra es
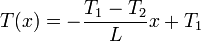
La temperatura varía linealmente desde la más alta hasta la mas baja. Hay que señalar que en el resultado final no aparece la conductividad térmica. Esto se debe a que la barra es homogénea.
2.2 Barras homogéneas en contacto
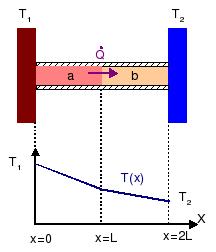
Consideremos ahora el caso del problema. Si T1 > T2, la energía fluirá desde la izquierda hacia la derecha. En condiciones estacionarias, de nuevo la potencia de energía transferida debe ser la misma en todos los puntos del sistema.
Nuestro objetivo ahora es encontrar la distribución de temperaturas T(x) en el conjunto de las dos barras. Como cada una de las dos barras tiene características físicas distintas (en concreto, la conductividad térmica), la función T(x) tendrá una expresión diferente según que estemos en una barra u otra. Escogemos el eje X como se indica en la figura. Llamando a a la barra de oro y b a la de plata tenemos
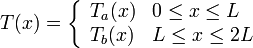
Partiendo de la base del apartado anterior, como cada barra es un medio homogéneo, supondremos que la distribución de temperaturas es lineal en cada barra, es decir
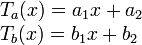
Tenemos cuatro constantes que hay determinar. Para encontrar cuanto valen imponemos las condiciones físicas del problema (técnicamente se llaman las condiciones de contorno)
Por un lado, las temperaturas en los extremos deben ser T1 y T2. Entonces
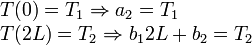
Por otro lado la temperatura debe variar de modo continuo al pasar de una barra a la otra. Esto impone la condición
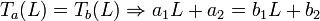
Finalmente, en condiciones estacionarias la potencia transferida debe ser la misma en todos los puntos del sistema. Esta potencia es
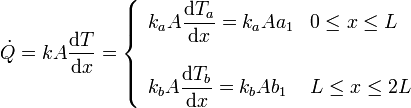
En el punto de contacto el flujo de energía que llega por la izquierda debe ser igual al que sale por la derecha. Por tanto
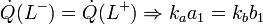
De este modo obtenemos cuatro ecuaciones que determinan las cuatro constantes en función de los datos del problema. La solución del sistema de ecuaciones es
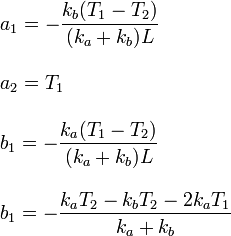
Para obtener la temperatura en el punto de contacto podemos usar Ta(x)
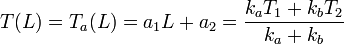
Podemos verificar que el resultado es razonable considerando la situación en que las dos barras tienen la misma conductividad térmica. Entonces el problema se reduciría al de la barra homogénea del apartado anterior, y la temperatura en el punto medio debería ser la media de las temperaturas en los extremos. Podemos comprobar que si ka = kb entonces obtenemos T(L) = (T1 + T2) / 2.
Sustituyendo los valores numéricos dados por el problema tenemos
T(L) = 51.2oC