Magnetización
De Laplace
Contenido |
1 Introducción
Los medios materiales perciben y producen campos magnéticos debido a la presencia de dipolos magnéticos en su interior. Cada átomo y cada partícula subatómica poseen un pequeño momento magnético dipolar.
1.1 Dipolos orbitales
En el modelo atómico de Bohr, el electrón orbita alrededor del núcleo, lo que se puede considerar una pequeña espira.
En la mecánica cuántica moderna, no hay tal órbita, pero asimismo se cumple que existe un momento magnético proporcional al momento angular del electrón (propiedad asociada a la rotación).
1.2 Dipolos intrínsecos
Todas las partículas poseen además un momento magnético propio, proporcional a su momento angular intrínseco (el espín).
Este momento magnético es una propiedad característica de cada partícula, como su carga o su masa, y no está asociado a una corriente eléctrica.
2 Definición
Para caracterizar estos momentos magnéticos se define su densidad, de forma análoga a como se hace con la densidad de carga eléctrica, la densidad de corriente eléctrica o la polarización. Dado un pequeño elemento de volumen Δτ, lo suficientemente pequeño para ser microscópico, pero lo suficientemente grande como para contener miles de partículas, se define la magnetización (o imanación, o imantación) como
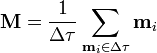
Esta magnetización es una función de la posición 
, considerando como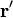 
la posición del elemento de volumen.
3 Unidades
De la definición se tiene que
![[M]= \frac{[m]}{[\tau]} = \frac{1\,\mathrm{A}\cdot\mathrm{m}^2}{\mathrm{m}^3}= \frac{1\,\mathrm{A}}{\mathrm{m}}](/wiki/images/math/9/3/2/9329a246ad58e099d8c7204838034dae.png)
