Extract from "General Relativity"

De Laplace

Revisión a fecha de 11:31 26 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Thermodynamics
2
3
4

1 Thermodynamics

Thermodynamical systems can be extraordinarily complicated; for example, a great number of processes can be going on in a star simultaneously. We want to try to explain the basic general ideas, restricting ourselves to the simplest systems.

During thermodynamical processes certain elements of matter, with their properties, remain conserved, for example, in non-relativistic thermodynamics molecules or atoms and their masses. In the course of transformations in star or during nuclear processes the baryons with their rest mass are conserved instead. We shall therefore relate all quantities to these baryons. If, for example, we choose a volume element of the system, then we shall take as four-velocity $u i$ of this element the average baryon velocity. The flow (motion) of the system will therefore be characterized by a four-velocity field

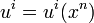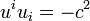
$u^i = u^i(x^n)\,$ , $u^iu_i=-c^2\,$

2

To set up the basic thermodynamical equations one first go to the local rest system

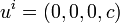
$u^i = (0,0,0,c)\,$

of the volume element under consideration and regard this volume element as a system existing in equilibrium (of course it interacts with its surroundings, so that the whole system is not necessarily in equilibrium); that is one introduces for this volume element the fundamental thermodynamic state variables, for example,

$n\,$ baryon number density,
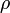$\rho\,$ baryon mass density,
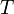$T\,$ temperature,
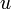$u\,$ internal energy per unit mass,
$s\,$ entropy per baryon mass,
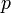$p\,$ isotropic pressure,
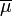$\overline{\mu}\,$ chemical potential,
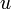$u\,$ free energy per unit mass.

3

"Density" here always means "per three-dimensional volume in the local rest system"; the entropy density, for example, would be given by $s ρ$ . There exist relationships between state variables which in the simplest case express the fact that only two of them are really independent, and from, knowledge of the entropy as a function of the energy and the density, or of the specific volume $v = 1 / ρ$ ,

$s = s(u,v)\,$

one can calculate the other quantities, for example,

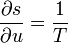
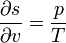
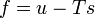$\frac{\partial s}{\partial u}=\frac{1}{T}$ $\frac{\partial s}{\partial v}=\frac{p}{T}$ $f=u-Ts\,$ etc.

4

For the interaction of the volume element we have balance equations. These are the law of conservation of baryon number

$(\rho u^n)_{;n}=0\,$

(generalized mass conservation), the balance equation for energy and momentum, formulated as the vanishing of the divergence of the energy-momentum tensor 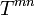$T^{mn}\,$ ,

$T^{mn}_{;n}=0\,$

Extract from "General Relativity"

De Laplace

Contenido

1 Thermodynamics

2

3

4

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES