Definición de sistemas de coordenadas
De Laplace
Contenido |
1 Introducción
El electromagnetismo clásico se describe mediante campos vectoriales, esto es, vectores que tienen un valor diferente en cada punto del espacio.
Las ecuaciones de Maxwell se describen de forma idónea mediante el llamado espaciotiempo de Minkowski, en el cual las tres dimensiones espaciales y el tiempo aparecen unidas en un solo sistema de referencia. No obstante, para los contenidos de este curso es suficiente con la descripción tradicional en la que por un lado tenemos un espacio tridimensional y por otro una línea temporal.
Por ello, un paso previo a la definición de campo vectorial es la caracterización del propio espacio. Supondremos igualmente un espacio tridimensional euclídeo. Por ello, en cada punto del espacio podemos definir un sistema de referencia con origen en dicho punto y formado por tres ejes ortogonales que se extienden indefinidamente, conservando su perpendicularidad.
2 Definición
El espacio se compone de puntos y para describir los puntos y distinguirlos unos de otros necesitamos ponerle un nombre a cada uno. Un sistema de nombres que identifica de forma individual a cada punto del espacio se denomina un sistema de coordenadas. Existen infinitos posibles sistemas de coordenadas. Sin embargo, para que un sistema de coordenadas sea útil para el cálculo, debe cumplir una serie de requisitos:
- Las coordenadas deben ser funciones numéricas de la posición.
- En el espacio tridimensional ordinario, una terna de coordenadas
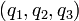 debe corresponder de forma unívoca a un punto.
debe corresponder de forma unívoca a un punto.
- En la medida de lo posible, cada punto debe venir representado por una sola terna de coordenadas.
- Las coordenadas deben ser funciones continuas y derivables de la posición, de forma que si un punto
 viene representado por la terna
viene representado por la terna 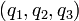 , un punto
, un punto 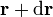 , infinitamente próximo, vendrá representado por
, infinitamente próximo, vendrá representado por 
Aun con esas limitaciones, el número de sistemas posibles sigue siendo infinito. Sin embargo, solo un subconjunto de ellos (los denominados sistemas ortogonales) cumple algunas propiedades adicionales que simplifican numerosos cálculos. Y dentro de las coordenadas ortogonales, tres sistemas destacan por su sencillez: las coordenadas cartesianas, las cilíndricas y las esféricas. En lo que sigue, nos limitaremos a considerar exclusivamente estos tres sistemas.
2.1 Coordenadas literales
El uso de letras en lugar de números para representar las posiciones no tiene nada de especial.
De hecho, un mapa no es más que una representación del espacio (o de la superficie terrestre, para ser precisos), en los que los puntos son etiquetados con los nombres de las poblaciones o accidentes geográficos.
3 Enlaces
- Siguiente: Coordenadas cartesianas. Definición