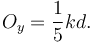De Laplace

Revisión a fecha de 14:51 18 feb 2021; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Posición de equilibrio
- 2.2 Fuerza vincular en O

1 Enunciado

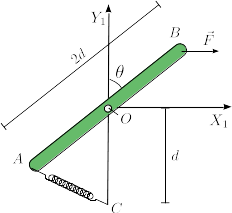
Una barra de longitud $2 d$ está articulada en su punto central en el punto fijo $O$ . El extremo $A$ se conecta al punto fijo $C$ por un muelle de constante elástica $k$ y longitud natural nula. Una fuerza 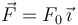$\vec{F}=F_0\,\vec{\imath}$ , con $F 0 > 0$ , se aplica en el punto $B$ . No se tiene en cuenta la fuerza de la gravedad.

Usando el Principio de los Trabajos Virtuales (PTV) (o el de las potencias virtuales, PPV) determina el valor de equilibrio del ángulo $θ$ .
Si el ángulo es tal que 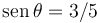$\,\mathrm{sen}\,{\theta}=3/5$ y $cosθ = 4 / 5$ , determina, usando el Principio de Liberación y el PTV (o el PPV), las componentes de la fuerza de reacción vincular en $O$ (en la base de los ejes de la figura)

2 Solución

2.1 Posición de equilibrio

2.1.1 Con el Principio de los Trabajos Virtuales

Las fuerzas activas que actúan sobre la barra son la fuerza aplicada en $B$ y la fuerza que el muelle ejerce en $A$ . El Principio de los Trabajos Virtuales (PTV) dice que, para que haya equilibrio, en cualquier desplazamiento virtual debe cumplirse

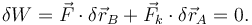
$\delta W = \vec{F}\cdot\delta\vec{r}_B + \vec{F}_k\cdot\delta\vec{r}_A = 0.$

Calculemos cada uno de esos términos. El sistema tiene un grado de libertad: ${θ}$ . Así pues, un desplazamiento virtual arbitrario es ${δθ}$ .

Para la fuerza en $B$ tenemos

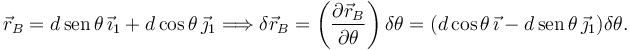
$\vec{r}_B = d\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + d\cos\theta\,\vec{\jmath}_1 \Longrightarrow \delta\vec{r}_B = \left(\dfrac{\partial\vec{r}_B}{\partial\theta}\right)\delta\theta = (d\cos\theta\,\vec{\imath} - d\,\mathrm{sen}\,\theta\,\vec{\jmath}_1)\delta\theta.$

Por tanto

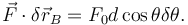
$\vec{F}\cdot\delta\vec{r}_B = F_0d\cos\theta\delta\theta.$

La fuerza del muelle sobre el extremo $A$ de la barra viene dada por

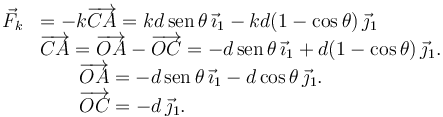
$\begin{array}{ll} \vec{F}_k & = -k\overrightarrow{CA} =kd\,\mathrm{sen}\,\theta\,\vec{\imath}_1 - kd(1-\cos\theta)\,\vec{\jmath}_1 \\ & \overrightarrow{CA} = \overrightarrow{OA} - \overrightarrow{OC} = -d\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + d(1-\cos\theta)\,\vec{\jmath}_1. \\ & \qquad \overrightarrow{OA} = -d\,\mathrm{sen}\,\theta\,\vec{\imath}_1 - d\cos\theta\,\vec{\jmath}_1.\\ & \qquad \overrightarrow{OC} = -d\,\vec{\jmath}_1. \end{array}$

Tenemos

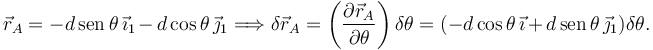
$\vec{r}_A = -d\,\mathrm{sen}\,\theta\,\vec{\imath}_1 - d\cos\theta\,\vec{\jmath}_1 \Longrightarrow \delta\vec{r}_A = \left(\dfrac{\partial\vec{r}_A}{\partial\theta}\right)\delta\theta = (-d\cos\theta\,\vec{\imath} + d\,\mathrm{sen}\,\theta\,\vec{\jmath}_1)\delta\theta.$

Por tanto

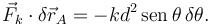
$\vec{F}_k\cdot\delta\vec{r}_A = -kd^2\,\mathrm{sen}\,\theta\,\delta\theta.$

Por tanto la condición de equilibrio es, para todo $δθ$ ,

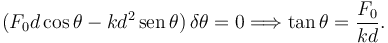
$(F_0d\cos\theta - kd^2\,\mathrm{sen}\,\theta)\,\delta\theta = 0 \Longrightarrow \tan\theta = \dfrac{F_0}{kd}.$

2.1.2 Con el Principio de las Potencias Virtuales

En esta caso necesitamos la reducción cinemática del movimiento de la barra

$\vec{\omega} = -\dot{\theta}\,\vec{k}, \qquad \vec{v}^{\,O} = \vec{0}.$

El Principio dice que, en cualquier desplazamiento virtual 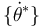$\{\dot{\theta}^*\}$ , debe cumplirse

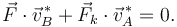
$\vec{F}\cdot\vec{v}^{\,*}_B + \vec{F}_k\cdot\vec{v}^{\,*}_A=0.$

Las velocidades que necesitamos son

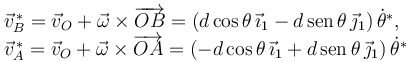
$\begin{array}{l} \vec{v}^{\,*}_B = \vec{v}_O + \vec{\omega}\times\overrightarrow{OB} = (d\cos\theta\,\vec{\imath}_1 - d\,\mathrm{sen}\,\theta\,\vec{\jmath}_1)\,\dot{\theta}^*,\\ \vec{v}^{\,*}_A = \vec{v}_O + \vec{\omega}\times\overrightarrow{OA} = (-d\cos\theta\,\vec{\imath}_1 + d\,\mathrm{sen}\,\theta\,\vec{\jmath}_1)\,\dot{\theta}^* \end{array}$

Aplicando el PPV llegamos a la misma condición que en el caso anterior.

2.1.3 Con la energía potencial

Otra forma de hacerlo es usando la energía potencial. La acción del muelle puede describirse con la energía potencial

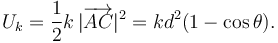
$U_k = \dfrac{1}{2}k\,|\overrightarrow{AC}|^2 = kd^2(1-\cos\theta).$

La acción de $\vec{F}$ se describe con una fuerza generalizada

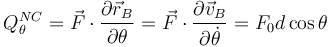
$Q^{NC}_{\theta} = \vec{F}\cdot\dfrac{\partial \vec{r}_B}{\partial \theta} = \vec{F}\cdot\dfrac{\partial \vec{v}_B}{\partial \dot{\theta}} = F_0d\cos\theta$

La condición de equilibrio es

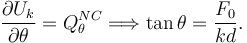
$\dfrac{\partial U_k}{\partial \theta} = Q^{NC}_{\theta} \Longrightarrow \tan\theta = \dfrac{F_0}{kd}.$

2.2 Fuerza vincular en $O$

La fuerza vincular en $O$ garantiza que se cumpla el vínculo 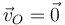$\vec{v}_O=\vec{0}$ . Por tanto debe tener dos componentes (es un sistema plano)

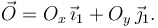
$\vec{O} = O_x\,\vec{\imath}_1 + O_y\,\vec{\jmath}_1.$

Por tanto, tenemos que aplicar el Principio de Liberación dos veces.

Componente $O x$

Liberamos la barra de modo que su centro pueda desplazarse horizontalmente. Ahora hay dos grados de libertad: ${x O,θ}$ y un desplazamiento virtual genérico tiene la forma ${δ x O,δθ}$ . Al liberar, tenemos que introducir una fuerza 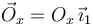$\vec{O}_x = O_x\,\vec{\imath}_1$ que se comporta como una fuerza activa. El PTV dice que, para cualquier desplazamiento virtual, en equilibrio debe cumplirse

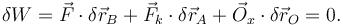
$\delta W = \vec{F}\cdot\delta\vec{r}_B + \vec{F}_k\cdot\delta\vec{r}_A + \vec{O}_x\cdot\delta\vec{r}_O=0.$

De todos los desplazamientos virtuales posibles escogemos el que cumple

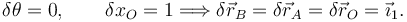
$\delta\theta = 0, \qquad \delta x_O = 1 \Longrightarrow \delta\vec{r}_B = \delta\vec{r}_A = \delta\vec{r}_O = \vec{\imath}_1.$

Aplicando el PTV llegamos a

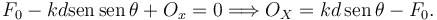
$F_0 - kd\mathrm{sen}\,\mathrm{sen}\,\theta + O_x=0 \Longrightarrow O_X = kd\,\mathrm{sen}\,\theta - F_0.$

Usando el valor de $θ$ dado por el enunciado tenemos finalmente

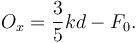
$O_x = \dfrac{3}{5}kd-F_0.$

Componente $O y$

Ahora liberamos la barra de modo que su centro pueda desplazarse verticalmente. Los dos grados de libertad son: ${y O,θ}$ y un desplazamiento virtual genérico tiene la forma ${δ y O,δθ}$ . Al liberar, tenemos que introducir una fuerza 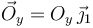$\vec{O}_y = O_y\,\vec{\jmath}_1$ que se comporta como una fuerza activa. El PTV dice que, para cualquier desplazamiento virtual, en equilibrio debe cumplirse

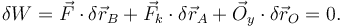
$\delta W = \vec{F}\cdot\delta\vec{r}_B + \vec{F}_k\cdot\delta\vec{r}_A + \vec{O}_y\cdot\delta\vec{r}_O=0.$

De todos los desplazamientos virtuales posibles escogemos el que cumple

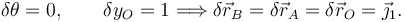
$\delta\theta = 0, \qquad \delta y_O = 1 \Longrightarrow \delta\vec{r}_B = \delta\vec{r}_A = \delta\vec{r}_O = \vec{\jmath}_1.$

Aplicando el PTV llegamos a

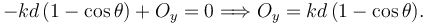
$-kd\,(1-\cos\theta) + O_y=0 \Longrightarrow O_y = kd\,(1-\cos\theta).$

Usando el valor de $θ$ dado por el enunciado tenemos finalmente

$O_y = \dfrac{1}{5}kd.$

Equilibrio de barra con muelle (Ene. 2021)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posición de equilibrio

2.1.1 Con el Principio de los Trabajos Virtuales

2.1.2 Con el Principio de las Potencias Virtuales

2.1.3 Con la energía potencial

2.2 Fuerza vincular en $O$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Equilibrio de barra con muelle (Ene. 2021)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posición de equilibrio

2.1.1 Con el Principio de los Trabajos Virtuales

2.1.2 Con el Principio de las Potencias Virtuales

2.1.3 Con la energía potencial

2.2 Fuerza vincular en O

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Fuerza vincular en $O$