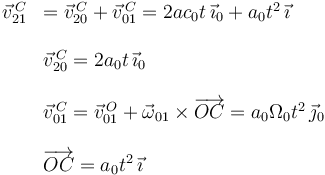De Laplace

Revisión a fecha de 19:00 13 feb 2021; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Solución
- 2.1 Reducciones cinemáticas
  - 2.1.1 Movimiento {01}
  - 2.1.2 Movimiento {20}
- 2.2 Movimiento {21}

1 Enunciado

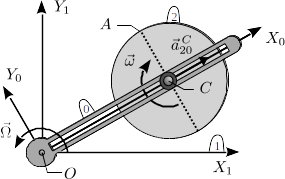
Una varilla recta y rígida (sólido "0") se mueve siempre contenida en el plano fijo $O X 1 Y 1$ (sólido "1"), girando, con velocidad angular constante $Ω$ y en el sentido indicado en la figura, alrededor de su extremo articulado el punto fijo $O$ . El centro $C$ de un disco de radio $R$ (sólido "2"), recorre la varilla alejándose con aceleración constante $2 a 0$ . En el instante inicial $t = 0$ , el punto $C$ coincidía con el $O$ y su velocidad era nula. A su vez, el disco gira alrededor de su centro $C$ en el sentido indicado, con velocidad angular constante $ω$ (respecto a la varilla) y permaneciendo siempre paralelo al plano fijo $O X 1 Y 1$ . En el instante inicial la varilla recta coincidía con el eje $O X 1$ ,

Determina reducciones cinemáticas y sus derivadas temporales de los movimientos {01}, {20} y {21}. Puedes hacerlo en cualquier punto.
En el instante $t = 1 / Ω$ , encuentra la posición de los C.I.R. de los tres movimientos.

2 Solución

2.1 Reducciones cinemáticas

2.1.1 Movimiento {01}

El movimiento {01} es plano. Del dibujo vemos

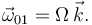
$\vec{\omega}_{01} = \Omega\,\vec{k}.$

Como $Ω$ es constante en el tiempo tenemos

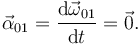
$\vec{\alpha}_{01} = \dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t} = \vec{0}.$

Por otro lado, el punto $O$ del sólido "0" coincide siempre con el punto $O$ del sólido "1" en todo instante de tiempo. Entonces

$\vec{v}^{\,O}_{01} = \vec{0}, \qquad \vec{a}^{\,O}_{01} = \vec{0}.$

Es decir, la reducción cinemática en $O$ de este movimiento es

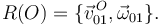
$R(O) = \{\vec{v}^{\,O}_{01}, \vec{\omega}_{01}\}.$

Su derivada temporal es

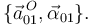
$\{\vec{a}^{\,O}_{01}, \vec{\alpha}_{01}\}.$

2.1.2 Movimiento {20}

Reducimos este movimiento en el punto $C$ . Como es plano, del dibujo vemos

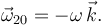
$\vec{\omega}_{20} = -\omega\,\vec{k}.$

Como $ω$ es constante en el tiempo tenemos

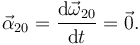
$\vec{\alpha}_{20} = \dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t} = \vec{0}.$

El punto $C$ del disco desliza sobre el eje $O X 0$ con aceleración uniforme

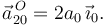
$\vec{a}^{\,O}_{20} = 2a_0\,\vec{\imath}_0.$

Como en el instante inicial el centro del disco estaba en $O$ y tenía velocidad nula tenemos

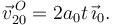
$\vec{v}^{\,O}_{20} = 2a_0t\,\vec{\imath}_0.$

Es decir, la reducción cinemática en $C$ de este movimiento es

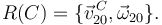
$R(C) = \{\vec{v}^{\,C}_{20}, \vec{\omega}_{20}\}.$

Su derivada temporal es

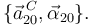
$\{\vec{a}^{\,C}_{20}, \vec{\alpha}_{20}\}.$

2.2 Movimiento {21}

Construimos este movimiento con la composición

${21} = {20} + {01}.$

Para la velocidad y aceleración angulares tenemos

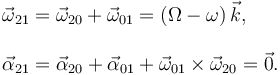
$\begin{array}{l} \vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = (\Omega-\omega)\,\vec{k},\\ \\ \vec{\alpha}_{21} = \vec{\alpha}_{20} + \vec{\alpha}_{01} + \vec{\omega}_{01}\times\vec{\omega}_{20} = \vec{0}. \end{array}$

Para la velocidad en $C$ tenemos

$\begin{array}{rl} \vec{v}^{\,C}_{21} & = \vec{v}^{\,C}_{20} + \vec{v}^{\,C}_{01} = 2ac_0t\,\vec{\imath}_0 + a_0t^2\,\vec{\imath}\\ &\\ &\vec{v}^{\,C}_{20} = 2a_0t\,\vec{\imath}_0\\ &\\ &\vec{v}^{\,C}_{01} = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OC} = a_0\Omega_0t^2\,\vec{\jmath}_0\\ &\\ &\overrightarrow{OC} = a_0t^2\,\vec{\imath} \end{array}$

Barra rotando con disco, Septiembre 2019 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducciones cinemáticas

2.1.1 Movimiento {01}

2.1.2 Movimiento {20}

2.2 Movimiento {21}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES