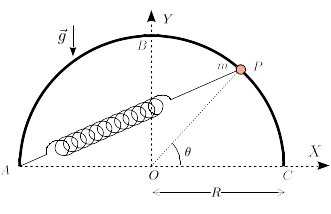
Partícula en semiaro circular con muelle (Ene. 2020 G.I.C.)
De Laplace
Contenido |
1 Enunciado
Una partícula de masa m está engarzada en un semiaro de radio R. Un muelle de constante elástica k = mg / R y longitud natural nula conecta la partícula y el punto A del semiaro. La gravedad actúa como se indica en la figura.
- Escribe los vectores de posición y velocidad de la partícula en la base vectorial cartesiana.
- Escribe la expresión que da la energía mecánica de la partícula para una posición arbitraria sobre el semiaro.
- En el instante inicial, la partícula se encuentra en el punto A. Se le da un empujón de modo que su rapidez es v0. Suponiendo que el contacto entre la partícula y el semiaro es liso, ¿cuanto debe valer v0 para que la partícula llegue hasta el punto B?
- Supongamos que el vínculo es rugoso. El trabajo que realiza el semiaro sobre la partícula es | WR | = λmgR, siendo λ una constante sin dimensiones. ¿Cuál es el valor mínimo de v0 para repetir el apartado anterior?
2 Solución
2.1 Vectores de posición y velocidad
El vector de posición es

El vector velocidad se obtiene derivando respecto del tiempo este vector
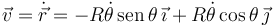
2.2 Energía mecánica
La energía mecánica es la suma de las energía cinética y potencial de la partícula. La energía cinética es

Hay dos contribuciones a la energía potencial: de la gravedad y del muelle. Para la energía potencial gravitatoria escogemos como origen de energía potencial la altura del eje OX. Entonces la energía potencial gravitatoria es
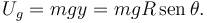
Para el muelle, como tiene longitud natural nula, la energía potencial elástica es
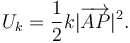
Podemos construir el vector 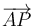 a partir de los vectores
a partir de los vectores  y
y  . Tenemos
. Tenemos
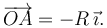
Entonces
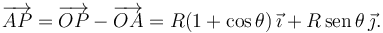
Podemos comprobar que este resultado es razonable imponiendo valores para θ
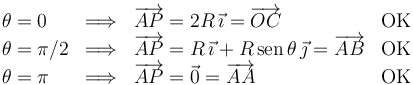
Ahora podemos escribir la expresión de la energía potencial elástica
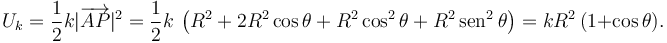
Con esto, la energía mecánica es
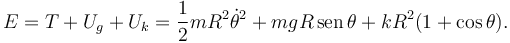
2.3 Movimiento sin rozamiento
Como no hay rozamiento, la energía mecánica se conserva a lo largo del movimiento de la partícula entre los puntos A y B. En el punto A se tiene θ = π y la partícula tiene rapidez inicial v0. Por tanto la energía mecánica es
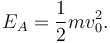
La condición mínima para que la partícula llegue a B es que su velocidad en este punto sea nula. En B tenemos θ = π / 2. Por tanto su energía mecánica es
EB = mgR + kR2.
El enunciado nos dice que k = mg / R. Entonces
EB = 2mgR.
Debe cumplirse
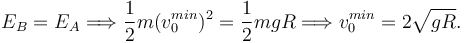
Es decir, la condición que debe cumplir v0 es
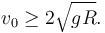
2.4 Movimiento con rozamiento
La presencia del rozamiento hace que la energía mecánica no se conserve. Pero como nos dan la magnitud del trabajo hecho por el rozamiento, podemos usar el balance de energía mecánica. El trabajo de rozamiento en este caso es negativo. Tenemos
EB − EA = WR = − | WR | = − λmgR.
Usando las expresiones del apartado anterior tenemos
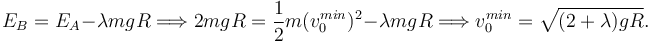
Por tanto, la condición es
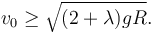
Este valor mínimo es mayor que el obtenido en el apartado anterior. Esto es lógico, pues en este problema la fuerza de rozamiento frena a la partícula.