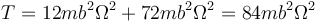Tres masas en un triángulo (CMR)
De Laplace
Contenido |
1 Tres masas en un triángulo
Un sólido rígido está formado por tres masas: una 5m, situada en O(0,0,0), una 4m, en A(3b,0,0) y una 3m, en B(0,4b,0).
- ¿En qué posición se encuentra el centro de masas del sistema?
- ¿Cuánto vale el tensor de inercia de este sólido respecto a unos ejes paralelos a OX, OY y OZ, por el centro de masas?
- Si el sólido está girando en torno a un eje que pasa por el CM y con velocidad angular
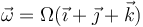 , calcule cuánto valen
, calcule cuánto valen
- su momento cinético respecto a G.
- su momento cinético respecto a O.
- su energía cinética.
2 Nota
Todas las velocidades se refieren al movimiento {21}, por lo que se omiten los subíndices.
3 Centro de masas
La posición del CM es la media ponderada de las posiciones de las tres masas
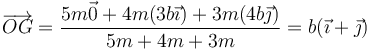
4 Tensor de inercia
Para hallar el tensor de inercia tenemos dos caminos.
- Directamente mediante las posiciones de las tres partículas respecto a los nuevos ejes.
- Hallando primero el tensor respecto a unos ejes por O y posteriormente aplicar el teorema de Steiner.
Veámoslo de las dos formas.
4.1 Directamente
La posición de las tres masas respecto al CM es, para O
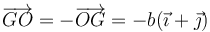
para A
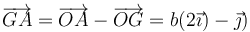
y para B
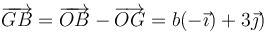
Aplicamos ahora la definición de tensor de inercia
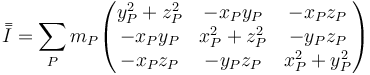
queda para la masa de O, de valor 5m
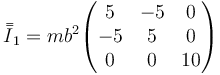
Para la de A, de valor 4m
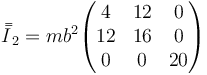
y para la de C, de valor 3m
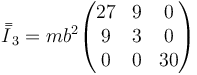
Sumando los tres tensores
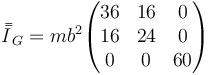
Este sería el código que lo hace en Mathematica (muy poco optimizado, pero para que se entienda mejor)
J[m_, P_] := m (P . P IdentityMatrix[3] - KroneckerProduct[P, P])
lm = {5 m, 4 m, 3 m}
mT = Sum[lm[[i]], {i, 3}]
OP = {{0, 0, 0}, {3 b, 0, 0}, {0, 4 b, 0}}
OG = Sum[lm[[i]] OP[[i]], {i, 3}]/mT
GP = Table[OP[[i]] - OG, {i, 3}]
IG = Sum[J[lm[[i]], GP[[i]]], {i, 3}]
MatrixForm[IG]
5 Mediante el teorema de Steiner
Si consideramos las posiciones respecto a los ejes de la figura, los tensores de inercia de cada masa resultan mucho más simples, por estar sobre los ejes.
Para la masa de O, de valor 5m
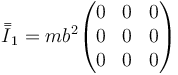
Para la de A, de valor 4m
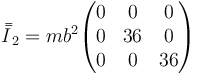
y para la de C, de valor 3m
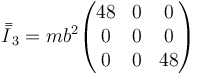
Sumando los tres tensores
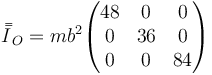
Por el teorema de Steiner, este tensor cumple
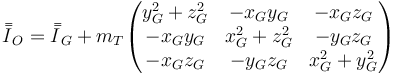
lo que nos da
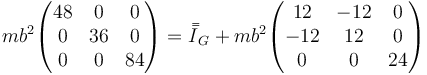
Despejamos y queda
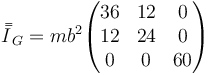
El código para este cálculo sería
J[m_, P_] := m (P . P IdentityMatrix[3] - KroneckerProduct[P, P])
lm = {5 m, 4 m, 3 m}
mT = Sum[lm[[i]], {i, 3}]
OP = {{0, 0, 0}, {3 b, 0, 0}, {0, 4 b, 0}}
OG = Sum[lm[[i]] OP[[i]], {i, 3}]/mT
IO = Sum[J[lm[[i]], OP[[i]]], {i, 3}]
IG = IO - J[mT, OG]
MatrixForm[IG]
6 Estado de rotación
6.1 Momento cinético respecto a G
El momento cinético se calcula como
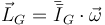
lo que nos da
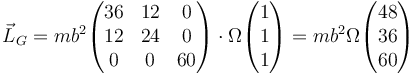
o en forma vectorial
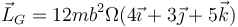
6.2 Momento cinético respecto a O
6.2.1 Por el teorema de König
Una forma de hallar el momento cinético respecto a O es mediante el teorema de König
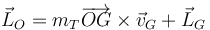
siendo la velocidad del CM
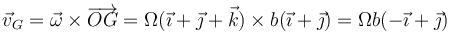
Por tanto,  vale
vale
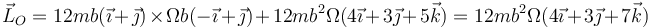
El código correspondería a añadir, tras las líneas de códigon anteriores
ω = Ω {1, 1, 1}
LG = IG . ω
vG = ω × OG
LO = mT OG × vG + LG
6.2.2 Directamente
En este caso, el punto O es fijo por hallarse en el eje de rotación. Por tanto, es mucho más fácil hallar el momento cinético directamente como
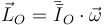
lo que nos da
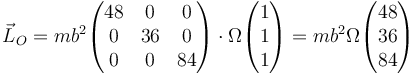
que queda, en forma vectorial
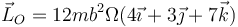
6.3 Energía cinética
6.3.1 Directamente
De nuevo, por ser O un punto fijo
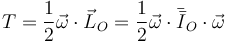
lo que nos da
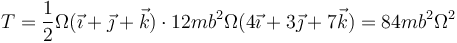
6.3.2 Por el teorema de König
En general, tanto si O es fijo como si no podemos recurrir al teorema de König
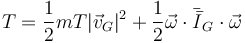
siendo la energía cinética de traslación
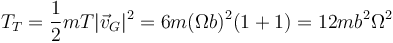
y la de rotación
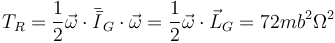
lo que da el total