Partícula en cono (CMR)

De Laplace

Enunciado

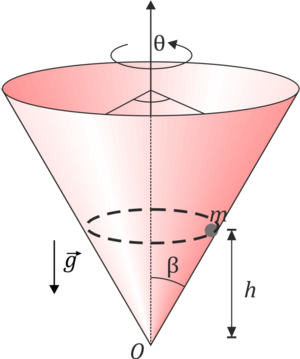
Una partícula está obligada a moverse por la superficie interior de un cono que tiene su vértice en el origen y que tiene un semiángulo de apertura β, es decir, la superficie del cono es, en cilíndricas z = ρ / tg(β). La partícula se mueve sin rozamiento por esta superficie y se halla sometida a la acción de la gravedad, que va en la dirección y sentido del eje OZ negativo

1. Obtenga las ecuaciones de movimiento para esta partícula, empleando como coordenadas las cilíndricas, introduciendo las fuerzas de reacción oportunas.
2. Reduzca este sistema a dos ecuaciones, una para la distancia al vértice, 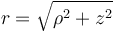y otra para el ángulo θ, de manera que no aparezcan ρ, z ni la tensión.
3. ¿A qué velocidad debe moverse la partícula si se desea que describa un movimiento circular horizontal, a una altura H respecto al vértice? ¿Cuánto vale la fuerza de reacción en ese caso?
4. Supongamos que parte de una altura H con una velocidad horizontal menor que la del apartado anterior. ¿Cuánto vale la mínima altura a la que llega la partícula?