Rotación y rodadura (CMR)
De Laplace
Contenido |
1 Rodadura
El caso de la rozadura sin deslizamiento es una situación frecuente de contacto entre sólidos. Cuando hay rodadura sin pivotamiento ni deslizamiento, quiere decir que, si se reduce el movimiento de uno de los sólidos respecto al otro en el punto de contacto A

es decir, la velocidad del punto de contacto es nula y la velocidad angular es puramente tangencial a la superficie de contacto. Desde el punto de vista cinemático, el movimiento de uno de los sólidos respecto al otro es una rotación respecto a un eje instantáneo que pasa por el punto de contacto y lleva la dirección de la velocidad angular.
Ahora bien, ¿cómo se produce la rodadura desde el punto de vista dinámico? En particular, ¿cómo es que es nula la velocidad del punto de contacto?
Para que haya rodadura, debe haber fricción que impida que un sólido deslice sobre el otro. Este rozamiento es estático, no dinámico, ya que la velocidad del punto de contacto es nula. Lo producen las irregularidades del suelo. Vendría a ser lo mismo que un engranaje, pero a escala microscópica
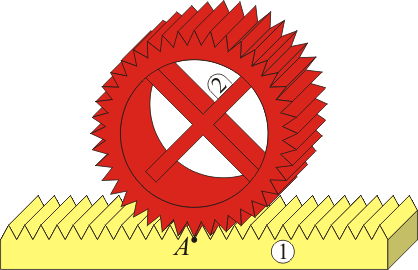
En el caso de una rueda dentada es claro que la velocidad del punto de contacto se anula. En el caso de la rodadura es lo mismo pero con “dientes” milimétricos o más pequeños. Por ello, la rodadura requiere contacto entre materiales abrasivos como goma sobre cemento, mientras que si las superficies de contacto están pulidas es más probable que se produzca deslizamiento.
El par cinemático de la rodadura impone que no haya velocidad en el punto de contacto, por lo que se anulan los tres grados de libertad de traslación, lo cual implica que en el punto de contacto se está ejerciendo una fuerza de reacción que puede tener cualquier dirección
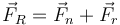
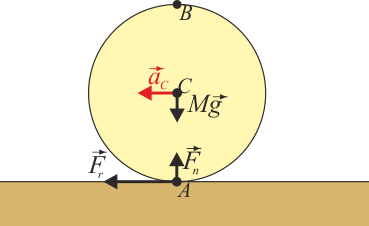
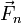 es la componente normal. Es una fuerza elástica debida a la impenetrabilidad de los sólidos.
es la componente normal. Es una fuerza elástica debida a la impenetrabilidad de los sólidos.  es la fuerza de rozamiento debida a la fricción seca entre las dos superficies. Puesto que se trata de rozamiento estático, debe cumplirse
es la fuerza de rozamiento debida a la fricción seca entre las dos superficies. Puesto que se trata de rozamiento estático, debe cumplirse

Esto establece limitaciones sobre la posibilidad de la rodadura. Por ejemplo, si un coche al circular pisa una placa de hielo, pierde el agarre al suelo no porque empiece a levitar, sino porque μ baja bruscamente, reduciendo la fuerza de rozamiento. Ello hace que se produzca deslizamiento en el punto de contacto y el coche patina.
La fuerza de reacción en el punto de contacto es de valor desconocido a priori (al menos la componente tangencial, para la cual solo podemos dar un valor máximo). Por ello, a la hora de analizar problemas en que hay rodadura, suele ser conveniente elegir como centro de reducción el punto de contacto. De esta forma, se anula el momento de las fuerzas aplicadas en este punto y desaparecen parcialmente del problema.
La fuerza de reacción por rodadura no realiza trabajo, ya que su potencia es nula

Esto quiere decir que la rodadura conserva la energía mecánica. ello permite resolver problemas como el de la rodadura por una pendiente analizando la conservación de la energía.
Si además se impide el pivotamiento, existe, junto a la fuerza, un par perpendicular a la superficie de contacto que impide este giro.
1.1 Rodadura libre
Para ilustrar lo anterior consideraremos brevemente el funcionamiento de una rueda. Suponemos un sólido de sección circular caracterizado por un momento de inercia respecto a un eje que pasa por su CM,
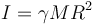
siendo 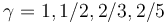 según se trate de un cilindro hueco o macizo, o una esfera hueca o maciza. También se puede generalizar sin problemas a otros sólidos circulares, como una corona cilíndrica, simplemente usando I en lugar de esta expresión particular.
según se trate de un cilindro hueco o macizo, o una esfera hueca o maciza. También se puede generalizar sin problemas a otros sólidos circulares, como una corona cilíndrica, simplemente usando I en lugar de esta expresión particular.
Suponemos que este sólido rueda sin deslizar sobre una superficie horizontal, sometida exclusivamente a la acción de su peso y a la reacción del suelo. Nos preguntamos entonces qué fuerza lo hace girar.
La cinemática de este movimiento es la siguiente. Tomando el eje X como el de avance y el Y el vertical, con el origen de coordenadas en el centro de la rueda, el movimiento es plano, con

 es el vector normal hacia afuera del plano, por tanto, si el giro es en sentido antihorario, ω es positiva, y si es horario negativa (regla de la mano derecha). La intuición nos dice que debe ser negativa. Esto se demuestra a partir de la condición de rodadura. Puesto que la velocidad del punto de contacto A es nula
es el vector normal hacia afuera del plano, por tanto, si el giro es en sentido antihorario, ω es positiva, y si es horario negativa (regla de la mano derecha). La intuición nos dice que debe ser negativa. Esto se demuestra a partir de la condición de rodadura. Puesto que la velocidad del punto de contacto A es nula
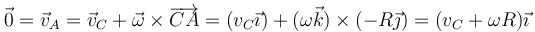
por lo cual
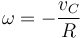
(nótese que se trata de una relación entre componentes, no entre vectores; la velocidad angular no es paralela a la lineal). Puesto que esta relación se cumple en todo instante, podemos derivarla respecto al tiempo y obtener una relación entre las aceleraciones

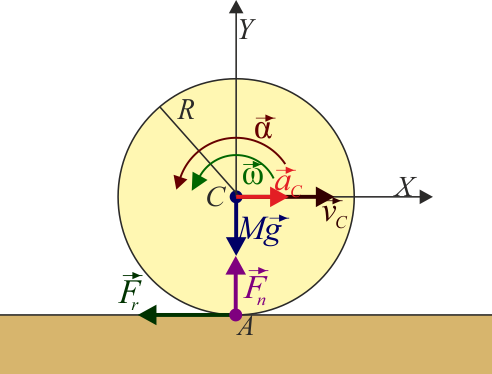
Veamos ahora la dinámica del sistema. Suponemos, de acuerdo con lo anterior, que habrá una fuerza de rozamiento estático entre el suelo y la rueda, que irá en sentido opuesto al movimiento. También imaginamos que esta fuerza de rozamiento frenará la rueda progresivamente. La ecuación para la aceleración del CM es
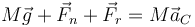
Separando en componentes
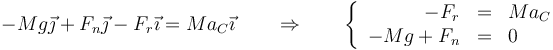
con lo cual ya sabemos el valor de la fuerza normal, Fn = Mg pero aun ignoramos el de la de rozamiento (ya que no conocemos cuánto es la aceleración del CM).
Necesitamos además la ecuación del momento de las fuerzas

De estas tres fuerzas, el peso no tiene momento, por estar aplicado en el propio CM; la fuerza normal tampoco, por estar el CM sobre la recta soporte de esta fuerza (es decir, porque 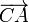 y
y 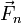 son vectores paralelos); queda la fuerza de rozamiento, que si va hacia atrás produce un giro horario. Su momento es igual al valor de la fuerza multiplicada por la distancia a la recta soporte, siendo esta distancia igual al radio de la rueda. Esto da
son vectores paralelos); queda la fuerza de rozamiento, que si va hacia atrás produce un giro horario. Su momento es igual al valor de la fuerza multiplicada por la distancia a la recta soporte, siendo esta distancia igual al radio de la rueda. Esto da

Sustituyendo lo que vale α
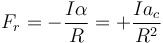
Tenemos entonces las ecuaciones
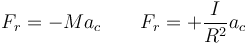
Según la primera de ellas, la fuerza de rozamiento frena la rueda, reduciendo la velocidad del CM; pero según la segunda, produce un giro cada vez mayor, acelerando el CM.

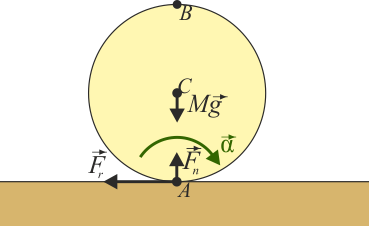
Estas dos conclusiones son contradictorias. La solución del sistema es realmente

es decir, para una rueda que va por un plano horizontal, no hay fuerza de rozamiento y la rueda no se frena, sino que continúa moviéndose a velocidad constante.
Esto es lo que hace de la rueda una invención magistral, ya que para llevar una carga deslizando sí hay que ejercer una fuerza que venza a la de rozamiento, pero para llevarla rodando no hace falta (teóricamente; sí existe un pequeño rozamiento por rodadura debido a que los sólidos reales no son rígidos).
1.2 Rodadura con fuerza aplicada
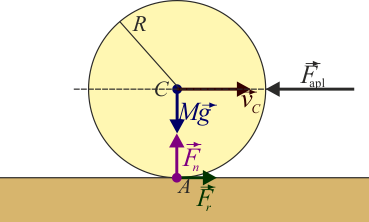
Supongamos ahora la misma rueda del ejemplo anterior, pero sometida a una fuerza horizontal en la dirección de movimiento. Esta fuerza puede ser, por ejemplo, el empuje debido a un motor o puede ser también negativa, como sería el caso de un ciclista que experimenta la fuerza de rozamiento viscoso con el aire.
Si esta fuerza está distribuida uniformemente sobre todo el frontal, podemos sustituirla por una sola equivalente, aplicada en el CM (como ocurre con el peso, pero ahora horizontal)

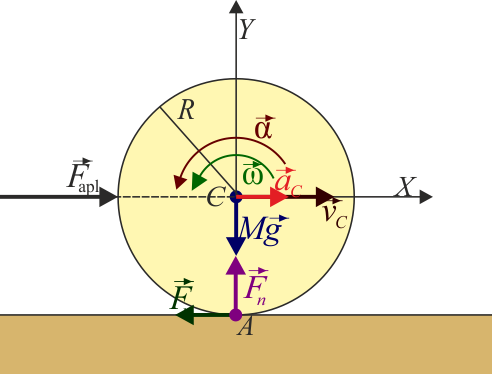
La inclusión de esta fuerza modifica las ecuaciones anteriores. Para las fuerzas
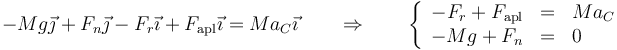
y para los momentos
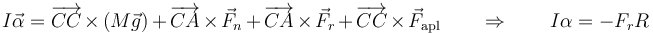
La nueva fuerza no añade momento alguno porque la consideramos aplicada en la línea que pasa por el CM. Un problema diferente sería, por ejemplo, el de un golpe a una bola de billar que se aplica por encima o debajo del CM.
Como se sigue cumpliendo la misma relación entre las aceleraciones

obtenemos
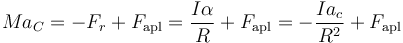
De aquí despejamos la aceleración del CM

que para el caso de los cuatro cuerpos considerados con I = γMR2 se reduce a
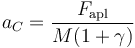
Puesto que γ > 0, esto quiere decir que la aceleración que adquiere el CM es menor que la que tendría un bloque sin rozamiento sometido a la fuerza aplicada.
El valor de la fuerza de rozamiento estático entre la rueda y el suelo vale
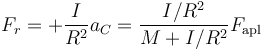
En forma vectorial
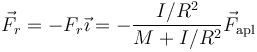
Observemos que la fuerza, al ser de rozamiento estático, se opone a la fuerza aplicada. Por tanto, en el caso de una rueda que avanza sometida a un rozamiento con el aire, la fuerza de rozamiento con el suelo va hacia adelante, es decir, en el mismo sentido que la velocidad del centro de la rueda. Para explicar como es que en este caso el rozamiento parece favorecer el movimiento, en vez de oponerse a él, hay que recordar que en el punto contacto la velocidad es nula, por lo que la fuerza aplicada tiende a desplazar este punto en su propio sentido, y la fuerza de rozamiento a lo que se opone es a este desplazamiento del punto de contacto, no al del CM.
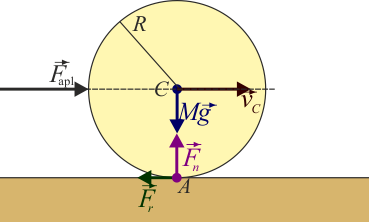
Para los cuatro cuerpos considerados
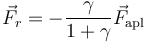
En particular, para el disco, γ = 1 / 2 y resulta una fuerza de 1/3 de la aplicada.
El límite de deslizamiento se alcanza cuando esta fuerza de rozamiento es igual, en módulo, a 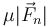 , lo que da una cota
, lo que da una cota
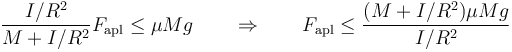
Una fuerza mayor que esta provoca que la rueda empiece a patinar. Esto es importante a la hora de estudiar el frenado de un vehículo, pues cuando las ruedas patinan se pierde el control de éste.
1.3 Rodadura con par aplicado
Empujar una rueda no es la única forma de que esta ruede. Consideremos el caso de la rueda trasera de una bicicleta. Esta rueda avanza porque tiene una cadena unida a ella a través de un piñón.
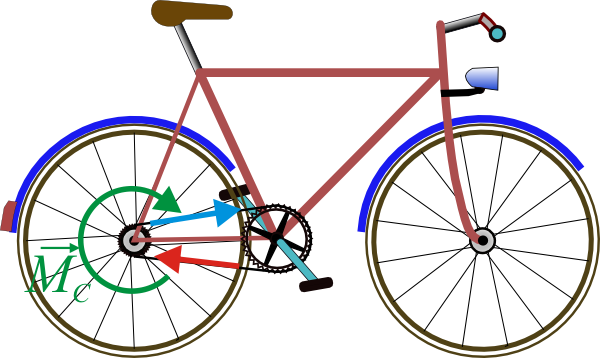
La cadena lo que hace sobre la rueda es ejercer un par de fuerzas. El tramo superior tira del piñón, mientras que el de abajo lo empuja. Si suponemos que estas dos fuerzas son paralelas e iguales en módulo 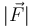 y el diámetro del piñón es D, el resultado es que sobre la rueda se aplica un momento en su centro
y el diámetro del piñón es D, el resultado es que sobre la rueda se aplica un momento en su centro
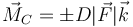
El signo es positivo cuando el par tiende a producir un giro antihorario alrededor del eje Z y negativo en caso contrario.
Si las fuerzas son diferentes en módulo o dirección, el sistema se reduce a la aplicación de una fuerza neta, de las consideradas en el apartado anterior, y a un par como éste, siendo la solución la superposición de los dos casos por separado.
El mismo principio de la rueda de la bicicleta se puede ver más fácil en el caso de un monociclo

Si los pedales tienen estribos, uno de los pies ejerce una fuerza hacia abajo y el otro hacia arriba. Al ser estas fuerzas verticales no producen aceleración horizontal. Sin embargo, la rueda avanza. ¿Quién la hace avanzar?
Supongamos una rueda sometida a un par de fuerzas

(el signo menos para que produzca un giro horario y haga avanzar la rueda hacia la derecha). Además de este par, actúan sobre ella el peso, la reacción normal y el rozamiento con el suelo horizontal. De estas fuerzas, la única horizontal es la de rozamiento. Por tanto, si la rueda avanza es porque el rozamiento la empuja. Es decir, estamos ante un caso en el que el rozamiento no se opone al movimiento, sino que es el que lo produce.
Es fácil ver por qué es así: Si no hubiera rozamiento, el par haría girar la rueda y esta patinaría sobre el suelo y en el punto de contacto se movería hacia atrás. Puesto que el rozamiento se opone el movimiento relativo, irá hacia adelante.
Si empleamos los mismos ejes que en el apartado anterior, el balance de fuerzas para esta rueda nos da las ecuaciones
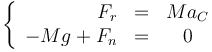
y el balance de momentos
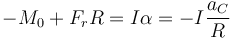
Sustituyendo la fuerza de rozamiento queda
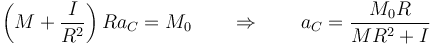
siendo la fuerza de rozamiento
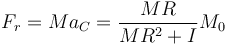
Vemos que efectivamente esta fuerza apunta en la dirección de avance de la rueda, no en el opuesto.
Para los cuatro cuerpos circulares que estamos considerando, la aceleración y esta fuerza se reducen a

El máximo par que podemos aplicar sin que la rueda patine lo da el coeficiente de rozamiento estático

1.4 Rozamiento por rodadura
En una situación ideal de dos sólidos perfectamente indeformables, la rodadura no disiparía ninguna energía, ya que el contacto se produciría en un solo punto, para el cual la velocidad es nula.
Sin embargo, todos los sólidos son deformables, y en el contacto de una rueda sobre el suelo éste no se produce en un solo punto, sino en una pequeña extensión (mayor cuanto más deformable sea la rueda). Dado que la rueda se encuentra en movimiento pero los puntos en contacto se hallan en reposo instantáneo, se producen esfuerzos en esos puntos, que disipan energía y producen rozamiento.
Además de la fuerza de rozamiento estático, aparece una fuerza de rozamiento por rodadura que obedece también la fórmula

El coeficiente de rozamiento, para ruedas poco deformables, puede ser estimado como
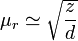
siendo d el diámetro de la rueda y z la “distancia de hundimiento”. Cuanto mayor sea ésta, mayor el rozamiento. Por ello es más barato enviar mercancías por ferrocarril que por camión.
Debido al rozamiento por rodadura hay que vigilar la presión de los neumáticos:
- Si es demasiado baja, aumenta el rozamiento y se consume una cantidad excesiva de energía
- Si es demasiado alta, se hace más difícil frenar un coche, ya que se reduce el área de contacto.






