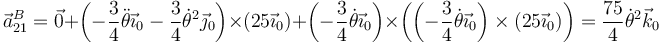Bola que rueda en carril (CMR)

De Laplace

Revisión a fecha de 13:29 2 dic 2020; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Grados de libertad
3 Ejes de rotación
4 Velocidades angulares
5 Aceleraciones angulares
6 Velocidad y aceleración de B
- 6.1 Velocidad en el movimiento {20}
- 6.2 Aceleración en el movimiento {21}

1 Enunciado

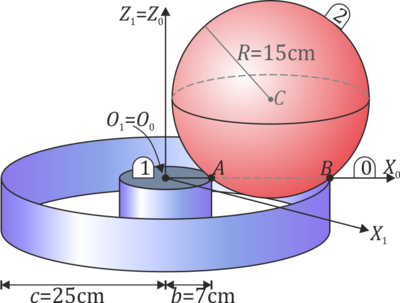
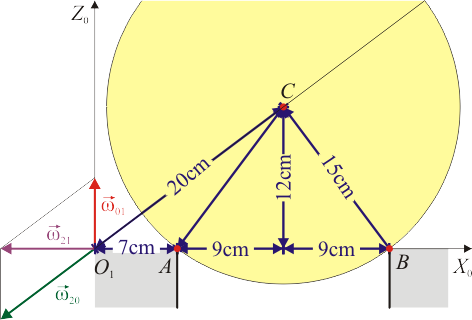
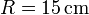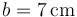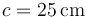Una bola (sólido “2”), de radio $R=15\,\mathrm{cm}$ , se desplaza sobre dos carriles circulares concéntricos fijos (sólido “1”), de radios $b=7\,\mathrm{cm}$ y $c=25\,\mathrm{cm}$ , situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que en todo instante, rueda sin deslizar sobre ambos carriles. Consideramos como sólido móvil intermedio (“sólido 0”) al plano $O 1 X 0 Z 0$ que contiene en todo instante al centro C de la esfera (ver figura).

¿Cuántos grados de libertad tiene este sistema?
Sea θ(t) el ángulo que forma el eje $O X 0$ con el $O X 1$ . Con ayuda del sólido intermedio halle los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
Halle las velocidades angulares y aceleraciones angulares de los movimientos {21}, {20} y {01}
Para el punto de la bola en contacto con el carril de mayor radio (punto B), determine 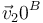$\vec{v}_20^B$ y $\vec{a}_{21}^B$ .

2 Grados de libertad

En principio, la esfera tiene 6 grados de libertad, pero debe cumplir los siguientes vínculos

Está apoyada sobre el carril, por lo que la altura del centro de la esfera es constante
La distancia de C al eje del sistema es constante.
La velocidad radial de un punto de contacto, A, es nula. Esto implica, por la condición de rigidez, que la velocidad de B, el otro punto de contacto también es nula, por lo que la segunda no es una condición aparte.
La velocidad tangencial al carril de A es nula.
La velocidad tangencial al carril de B es nula.

Tenemos 5 vínculos, lo que nos deja con un solo grado de libertad. Por ello, podemos describir el movimiento empleando una sola coordenada, el ángulo θ

3 Ejes de rotación

3.1 Movimiento {01}

El sólido “0” se limita a girar en torno al eje $O Z 1 = O Z 0$ . Por tanto, este es su eje de rotación, que además es permanente.

La velocidad angular de este movimiento es de la forma

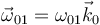
$\vec{\omega}_{01}=\omega_{01}\vec{k}_{0}$

3.2 Movimiento {21}

La esfera rueda apoyada en los puntos A y B, que tienen velocidad nula, por no haber deslizamiento. Por tanto el eje del movimiento pasa por estos dos puntos (y por el origen O, que se encuentra alineado con ellos). En el sistema “0” este eje es el $O X 0$ . Es un eje instantáneo, no permanente, ya que va girando con la esfera alrededor del $O Z 0$ . La velocidad angular del movimiento {21} es de la forma

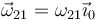
$\vec{\omega}_{21}=\omega_{21}\vec{\imath}_{0}$

3.3 Movimiento {20}

En el movimiento de la esfera, el centro C se encuentra en todo momento en la misma posición del sistema “0”. Concretamente, en cm,

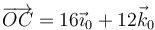
$\overrightarrow{OC}=16\vec{\imath}_0+12\vec{k}_0$

Por tanto

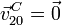
$\vec{v}^C_{20}=\vec{0}$

Por otro lado, el origen de coordenadas O pertenece tanto el eje del movimiento {21} como al del {01}, lo que implica que su velocidad en el movimiento {20} también es nula

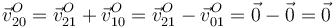
$\vec{v}^O_{20}=\vec{v}^O_{21}+\vec{v}^O_{10}=\vec{v}^O_{21}-\vec{v}^O_{01}=\vec{0}-\vec{0}=\vec{0}$

Por tanto, el eje del movimiento {20} es la recta que pasa por O y C. Es un eje permanente, pues en el sólido “0” su dirección es constante. La velocidad angular de este movimiento se podrá escribir como, normalizando,

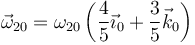
$\vec{\omega}_{20}=\omega_{20}\left(\frac{4}{5}\vec{\imath}_0+\frac{3}{5}\vec{k}_0\right)$

Aunque, como veremos, este resultado se puede obtener también de la ley de composición de velocidades angulares.

4 Velocidades angulares

Las dimensiones del sistema son las siguientes

4.1 Del movimiento {01}

La velocidad del movimiento {01} es la correspondiente a la variación del ángulo θ:

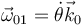
$\vec{\omega}_{01}=\dot{\theta}\vec{k}_0$

4.2 Del movimiento {21}

Obtenemos esta velocidad angular a partir de la velocidad del punto C, que es una articulación entre el sólido “0” y el “2” (ya que tiene una posición fija en ambos sólidos).

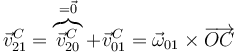
$\vec{v}^C_{21}=\overbrace{\vec{v}^C_{20}}^{=\vec{0}}+\vec{v}^{C}_{01}=\vec{\omega}_{01}\times\overrightarrow{OC}$

Sustituyendo los valores (todas las distancias en cm)

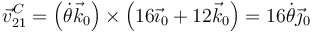
$\vec{v}^C_{21}=\left(\dot{\theta}\vec{k}_0\right)\times\left(16\vec{\imath}_0+12\vec{k}_0\right)=16\dot{\theta}\vec{\jmath}_0$

Esta velocidad, por su parte, corresponde también a la rotación alrededor del eje por A y B (y por O)

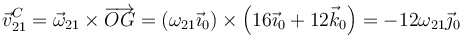
$\vec{v}^C_{21}=\vec{\omega}_{21}\times\overrightarrow{OG}=\left(\omega_{21}\vec{\imath}_0\right)\times\left(16\vec{\imath}_0+12\vec{k}_0\right)=-12\omega_{21}\vec{\jmath}_0$

Igualando esto a lo anterior queda

$\omega_{21}=-\frac{3}{4}\dot{\theta}\qquad\qquad\vec{\omega}_{21}=-\frac{3}{4}\dot{\theta}\vec{\imath}_0$

4.3 Del movimiento {20}

Por composición de velocidades angulares

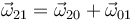
$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}$

Sustituimos lo que conocemos

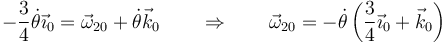
$-\frac{3}{4}\dot{\theta}\vec{\imath}_0 = \vec{\omega}_{20}+\dot{\theta}\vec{k}_0\qquad\Rightarrow\qquad \vec{\omega}_{20}=-\dot{\theta}\left(\frac{3}{4}\vec{\imath}_0+\vec{k}_0\right)$

Vemos que resulta un vector en la dirección de OC, sin necesidad de suponerlo previamente.

5 Aceleraciones angulares

5.1 Del movimiento {01}

El eje del movimiento {01} es uno permanente, ya que en todo momento coincide con $O Z 1$ . Esto quiere decir que cuando derivamos la velocidad angular para obtener la aceleración angular, el vector que la acompaña es una constante

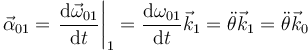
$\vec{\alpha}_{01}=\left.\frac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1=\frac{\mathrm{d}\omega_{01}}{\mathrm{d}t}\vec{k}_1=\ddot{\theta}\vec{k}_1=\ddot{\theta}\vec{k}_0$

5.2 Del movimiento {20}

El eje del movimiento {20}, que pasa por O y C también es permanente. Podría parecer que es instantáneo, ya que gira al moverse la esfera, pero eso solo ocurre si lo observamos desde el sistema “1”. La aceleración 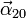$\vec{\alpha}_{20}$ es la derivada de $\vec{\omega}_{20}$ calculada en el sistema “0”, es decir, tratando los ejes de este sistema como fijos. Por ello, esta aceleración vale

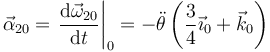
$\vec{\alpha}_{20}=\left.\frac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0=-\ddot{\theta}\left(\frac{3}{4}\vec{\imath}_0+\vec{k}_0\right)$

5.3 Del movimiento {21}

A diferencia de los dos anteriores, el eje del movimiento {21} es uno instantáneo, ya que desde el sistema “1” este eje sí que da vueltas en torno al eje $O Z 1$ .

Si derivamos teniendo en cuenta que los vectores de la base son función del tiempo

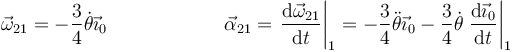
$\vec{\omega}_{21}=-\frac{3}{4}\dot{\theta}\vec{\imath}_0\qquad\qquad\qquad\vec{\alpha}_{21}=\left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1=-\frac{3}{4}\ddot{\theta}\vec{\imath}_0-\frac{3}{4}\dot{\theta}\left.\frac{\mathrm{d}\vec{\imath}_0}{\mathrm{d}t}\right|_1$

La derivada del vector de la base lo da la fórmula de Poisson

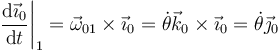
$\left.\frac{\mathrm{d}\vec{\imath}_0}{\mathrm{d}t}\right|_1=\vec{\omega}_{01}\times\vec{\imath}_0=\dot{\theta}\vec{k}_0\times\vec{\imath}_0=\dot{\theta}\vec{\jmath}_0$

con lo que llegamos a la aceleración angular

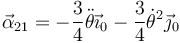
$\vec{\alpha}_{21}=-\frac{3}{4}\ddot{\theta}\vec{\imath}_0-\frac{3}{4}\dot{\theta}^2\vec{\jmath}_0$

Alternativamente, puede calcularse esta aceleración angular mediante la ley de composición de aceleraciones angulares

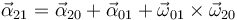
$\vec{\alpha}_{21}=\vec{\alpha}_{20}+\vec{\alpha}_{01}+\vec{\omega}_{01}\times\vec{\omega}_{20}$

donde ya conocemos cada uno de los términos

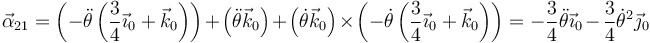
$\vec{\alpha}_{21}=\left(-\ddot{\theta}\left(\frac{3}{4}\vec{\imath}_0+\vec{k}_0\right)\right)+\left(\ddot{\theta}\vec{k}_0\right)+\left(\dot{\theta}\vec{k}_0\right)\times\left(-\dot{\theta}\left(\frac{3}{4}\vec{\imath}_0+\vec{k}_0\right)\right)= -\frac{3}{4}\ddot{\theta}\vec{\imath}_0-\frac{3}{4}\dot{\theta}^2\vec{\jmath}_0$

6 Velocidad y aceleración de B

El punto B se halla a 25cm del centro, en la misma línea en que está O y A, así que su posición es

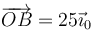
$\overrightarrow{OB}= 25\vec{\imath}_0$

6.1 Velocidad en el movimiento {20}

Para la velocidad de B usamos como centro de reducción el punto O, que es fijo en los tres movimientos, de manera que

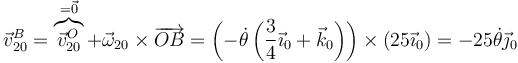
$\vec{v}^B_{20}=\overbrace{\vec{v}^O_{20}}^{=\vec{0}}+\vec{\omega}_{20}\times \overrightarrow{OB}=\left(-\dot{\theta}\left(\frac{3}{4}\vec{\imath}_0+\vec{k}_0\right)\right)\times\left(25\vec{\imath}_0\right)=-25\dot{\theta}\vec{\jmath}_0$

A esta velocidad se puede llegar observando que como su velocidad instantánea en el movimiento {21} es nula (ya que la bola rueda sin deslizar)

$\vec{0}=\vec{v}^B_{21}=\vec{v}^B_{20}+\vec{v}^B_{01}\qquad\Rightarrow\qquad \vec{v}^B_{20}=-\vec{v}^B_{01}$

y la velocidad en el movimiento {01} es simplemente una rotación en torno al eje $O Z 1$ .

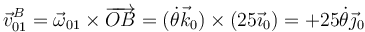
$\vec{v}^B_{01}=\vec{\omega}_{01}\times\overrightarrow{OB}=(\dot{\theta}\vec{k}_0)\times(25\vec{\imath}_0)=+25\dot{\theta}\vec{\jmath}_0$

y cambiando el sentido, llegamos al mismo resultado

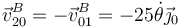
$\vec{v}^B_{20}=-\vec{v}^B_{01} = -25\dot{\theta}\vec{\jmath}_0$

6.2 Aceleración en el movimiento {21}

Tomando de nuevo como referencia a OB

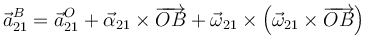
$\vec{a}^B_{21}=\vec{a}^O_{21}+\vec{\alpha}_{21}\times\overrightarrow{OB}+\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{OB}\right)$

Sustituímos cada términos

$\vec{a}^B_{21}=\vec{0}+\left(-\frac{3}{4}\ddot{\theta}\vec{\imath}_0-\frac{3}{4}\dot{\theta}^2\vec{\jmath}_0\right)\times\left(25\vec{\imath}_0\right)+\left(-\frac{3}{4}\dot{\theta}\vec{\imath}_0\right)\times\left(\left(-\frac{3}{4}\dot{\theta}\vec{\imath}_0\right)\times\left(25\vec{\imath}_0\right)\right)=\frac{75}{4}\dot{\theta}^2\vec{k}_0$

Bola que rueda en carril (CMR)

De Laplace

Contenido

1 Enunciado

2 Grados de libertad

3 Ejes de rotación

3.1 Movimiento {01}

3.2 Movimiento {21}

3.3 Movimiento {20}

4 Velocidades angulares

4.1 Del movimiento {01}

4.2 Del movimiento {21}

4.3 Del movimiento {20}

5 Aceleraciones angulares

5.1 Del movimiento {01}

5.2 Del movimiento {20}

5.3 Del movimiento {21}

6 Velocidad y aceleración de B

6.1 Velocidad en el movimiento {20}

6.2 Aceleración en el movimiento {21}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES