Masa en superficie horizontal con masa colgando verticalmente
De Laplace
Contenido |
1 Enunciado
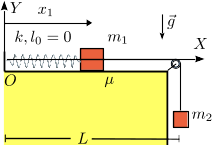
Dos masas puntuales m1 y m2 están unidas por una cuerda sin masa y longitud L, que desliza sobre una polea también sin masa, como se indica en la figura. La masa m1 está conectada a un muelle de constante elástica k y longitud natural nula. El otro extremo del muelle está anclado en el origen del sistema de referencia OXY.
- Suponiendo que no hay rozamiento, encuentra la posición de equilibrio del sistema.
- Si hay rozamiento entre m1 y la superfice horizontal, caracterizado por un coeficiente de rozamiento estático μ, encuentra el rango de posibles posiciones de equilibrio. Suponiendo m1 = kL / 4g y m2 = kL / 2g ¿que condición debe cumplir μ para que toda la superfice sea una posible posición de equilibrio?
- Encuentra la ecuación de movimiento de las dos masas suponiendo que no hay rozamiento.
- Calcula el vector de posición de las dos masas en función del tiempo si las condiciones iniciales son x1(0) = m2g / k y
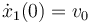 .
.
2 Solución
2.1 Posición de equilibrio sin rozamiento
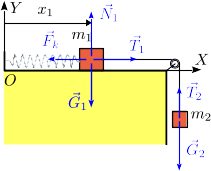
La figura de la derecha muestra las fuerzas que actúan sobre cada una de las masas. Para la masa 1 son: su peso 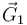 , la fuerza del muelle
, la fuerza del muelle 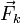 , la de la cuerda
, la de la cuerda 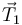 y la fuerza vincular ejercida por la superficie horizontal
y la fuerza vincular ejercida por la superficie horizontal 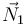 .
Para la masa 2 son su peso
.
Para la masa 2 son su peso 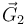 y la fuerza de la cuerda
y la fuerza de la cuerda 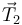 . Usando la base cartesiana asociada a los ejes de la figura estas fuerzas pueden expresarse así
. Usando la base cartesiana asociada a los ejes de la figura estas fuerzas pueden expresarse así
Masa 1
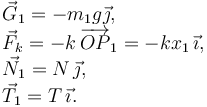
Masa 2
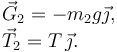
Hemos usado que, al ser la polea y la cuerda sin masa, la tensión se transmite a lo largo de la cuerda.
La condición de equilibrio es que la suma de las fuerzas sobre cada masa sea nula. Esto nos da 4 ecuaciones, pues el problema es bidimensional. Tenemos
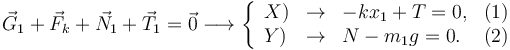
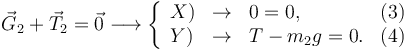
En este caso la ecuación (3) es superflua porque la masa 2 sólo tiene movimiento vertical.
Las incógnitas son {x1,N,T} y tenemos 3 ecuaciones. El problema tiene solución única y es
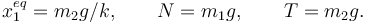
2.2 Posiciones de equilibrio con rozamiento
El diagrama de fuerzas de la derecha es similar al del apartado anterior. La diferencia es que hay que añadir una fuerza más sobre la masa 1, la de rozamiento que ejerce la superficie horizontal. Sólo conocemos a priori su dirección no el sentido. Tampoco conocemos su magnitude. Esta fuerza se expresa
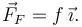
Las condiciones de equilibrio y las ecuaciones correspondiente son
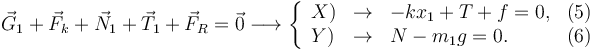
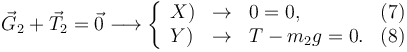
Ahora las magnitudes desconocidas son {x1,T,f,N}. Son 4. Y sólo tenemos 3 ecuaciones.
Lo que ocurre es que ahora la solución no es única. El rozamiento hace que haya varios valores posibles de x1 para los que las masas están en equilibrio. ¿Cómo afrontamos esta situación? Vamos a suponer que el valor de x1 es un dato. Vamos a llamarlo x1 = d. Si ahora d es un dato, las incógnitas son {T,f,N}. Podemos entonces calcular su valor con las ecuaciones (5), (6) y (8).
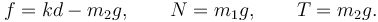
Con estos resultados las fuerzas vinculares que actúan sobre las masas, (usando los valores de m1 y m2 que se dan para este apartado)
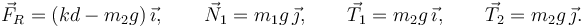
Esos son los valores de las fuerzas necesarios para que haya equilibrio. Ahora bien, esas cuatro fuerzas no se comportan igual. Las fuerzas 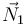 ,
, 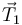 y
y 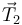 pueden ser tan grandes como haga falta, pues suponemos que las ligaduras a las que están asociadas se mantienen siempre. Pero la fuerza de rozamiento
pueden ser tan grandes como haga falta, pues suponemos que las ligaduras a las que están asociadas se mantienen siempre. Pero la fuerza de rozamiento  no se comporta igual. Esta fuerza tiene un módulo máximo que vale
no se comporta igual. Esta fuerza tiene un módulo máximo que vale
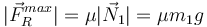
Es decir, el valor de la fuerza de rozamiento tiene que cumplir la condición
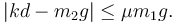
Utilizando los valores de m1 y m2 que se dan para este apartado esta condición queda
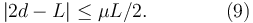
Debemos considerar dos situaciones posibles:
2d > L: En este caso se tiene que (2d − L) > 0, y por tanto | 2d − L | = 2d − L. Usándolo en (9) obtenemos
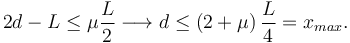
2d < L: En este caso se tiene que (2d − L) < 0, y por tanto | 2d − L | = − (2d − L) = L − 2d. Usándolo en (9) obtenemos
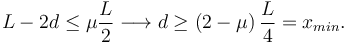
Es decir, para que la fuerza de rozamiento sea capaz de mantener el equilibrio deben cumplirse estas dos condiciones a la vez, lo que nos dice que el valor de d (que da el valor posible de equilibrio de x) debe cumplir
![d \in [x_{min}, x_{max}]](/wiki/images/math/7/e/0/7e0ede7c50dfd37037dc86cba08606b6.png)
¿Que pasa si 2d = L?. Esta posición corresponde al valor de 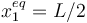 con los valores de las masas usados en este apartado. En este caso, la fuerza de rozamiento es cero pues no hace falta para mantener el equilibrio. Podemos entender ahora que significan las dos situaciones que hemos considerado. Si d < L / 2 la masa 1 estaría a la izquierda de la posición de equilibrio sin rozamiento. Entonces la fuerza del muelle sería menor que la fuerza que ejerce la cuerda y la fuerza de rozamiento apuntaría hacia la izquierda para compensar. Si d > L / 2 la masa 1 estaría a la derecha de la posición de equilibrio sin rozamiento y la fuerza ejercida por el muelle sería mayor que la de la cuerda y la fuerza de rozamiento apuntaría hacia la derecha para compensar.
con los valores de las masas usados en este apartado. En este caso, la fuerza de rozamiento es cero pues no hace falta para mantener el equilibrio. Podemos entender ahora que significan las dos situaciones que hemos considerado. Si d < L / 2 la masa 1 estaría a la izquierda de la posición de equilibrio sin rozamiento. Entonces la fuerza del muelle sería menor que la fuerza que ejerce la cuerda y la fuerza de rozamiento apuntaría hacia la izquierda para compensar. Si d > L / 2 la masa 1 estaría a la derecha de la posición de equilibrio sin rozamiento y la fuerza ejercida por el muelle sería mayor que la de la cuerda y la fuerza de rozamiento apuntaría hacia la derecha para compensar.
2.2.1 Condición para que toda la superficie horizontal sea de equilibrio
Para que esto ocurra debe cumplirse
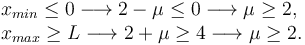
Por tanto, la condición sobre el coeficiente de rozamiento es
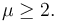
2.3 Movimiento sin rozamiento
Si no hay rozamiento el diagrama de fuerzas del primer apartado vuelve a ser válido. Lo que cambia ahora es que la ley física que tenemos que aplicar es la Segunda Ley de Newton. Hay que hacerlo para las dos masas por separado
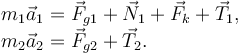
Tenemos que encontrar expresiones para las aceleraciones de las masas. Del dibujo de la derecha vemos que
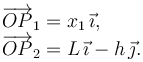
El enunciado dice que la longitud de la cuerda es L. Entonces se cumple
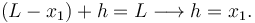
Entonces tenemos
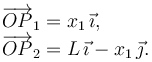
Derivamos una vez respecto al tiempo para obtener las velocidades
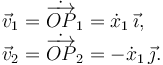
Derivamos otra vez respecto del tiempo para obtener las aceleraciones
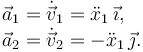
A partir de la Segunda Ley de Newton obtenemos
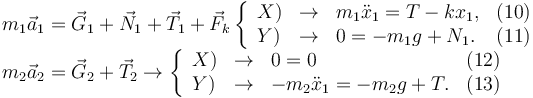
Sumando las ecuaciones (10) y (13) tenemos
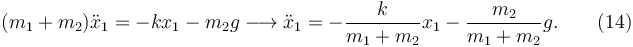
Esta es la ecuación de movimiento. Las ecuaciones (11) y (13) nos dan los valores de N1 y T:
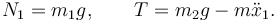
Es interesante destacar que T no es igual al peso de la masa 2. Esto sólo ocurre en situación de equilibrio estático, es decir, cuando 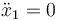 .
.
2.4 Solución para las condiciones iniciales dadas
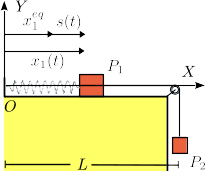
Para poner la ecuación (14) en una forma mas reconocible, usamos la distancia s para describir la posición de la masa 1 (ver figura de la derecha)
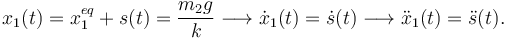
Sustituyendo estas expresiones de x1 y 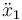 en la ecuación (14) obtenemos la ecuación diferencial
en la ecuación (14) obtenemos la ecuación diferencial
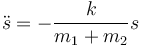
Esta ecuación tiene la forma
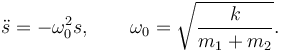
Corresponde a un movimiento armónico simple con período
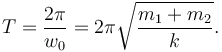
La solución general es de la forma
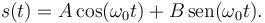
Las constantes A y B hay que determinarlas a partir de las condiciones iniciales. Las condiciones iniciales para s(t) son
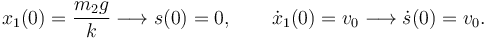
Aplicando estas condiciones obtenemos
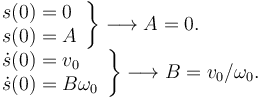
Por tanto, el movimiento de la masa 1 queda descrito por
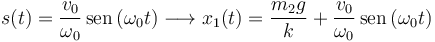
El movimiento de la masa 2 también queda determinado al conocer x1(t).