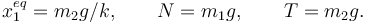1 Enunciado

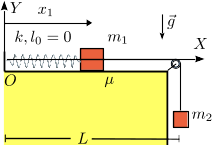
Dos masas puntuales $m 1$ y $m 2$ están unidas por una cuerda sin masa y longitud $L$ , que desliza sobre una polea también sin masa, como se indica en la figura. La masa $m 1$ está conectada a un muelle de constante elástica $k$ y longitud natural nula. El otro extremo del muelle está anclado en el origen del sistema de referencia $O X Y$ .

Suponiendo que no hay rozamiento, encuentra la posición de equilibrio del sistema.
Si hay rozamiento entre $m 1$ y la superfice horizontal, caracterizado por un coeficiente de rozamiento estático $μ$ , encuentra el rango de posibles posiciones de equilibrio. Suponiendo $m 1 = m 2 = k L / g$ , ¿que condición debe cumplir $μ$ para que toda la superfice sea una posible posición de equilibrio?
Encuentra la ecuación de movimiento de las dos masas suponiendo que no hay rozamiento.
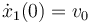Calcula el vector de posición de las dos masas en función del tiempo si las condiciones iniciales son $x 1 (0) = m 2 g / k$ y $\dot{x}_1(0)=v_0$ .

2 Solución

2.1 Posición de equilibrio

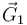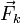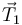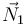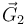La figura de la derecha muestra las fuerzas que actúan sobre cada una de las masas. Para la masa 1 son: su peso $\vec{G}_1$ , la fuerza del muelle $\vec{F}_k$ , la de la cuerda $\vec{T}_1$ y la fuerza vincular ejercida por la superficie horizontal $\vec{N}_1$ . Para la masa 2 son su peso $\vec{G}_2$ y la fuerza de la cuerda 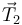$\vec{T}_2$ . Usando la base cartesiana asociada a los ejes de la figura estas fuerzas pueden expresarse así

Masa 1

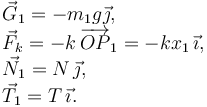
$\begin{array}{l} \vec{G}_1 = -m_1 g \vec{\jmath}, \\ \vec{F}_k = -k\,\overrightarrow{OP}_1 = -kx_1\,\vec{\imath},\\ \vec{N}_1 = N\,\vec{\jmath},\\ \vec{T}_1 = T\,\vec{\imath}. \end{array}$

Masa 2

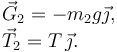
$\begin{array}{l} \vec{G}_2 = -m_2 g \vec{\jmath}, \\ \vec{T}_2 = T\,\vec{\jmath}. \end{array}$

Hemos usado que, al ser la polea y la cuerda sin masa, la tensión se transmite a lo largo de la cuerda.

La condición de equilibrio es que la suma de las fuerzas sobre cada masa sea nula. Esto nos da 4 ecuaciones, pues el problema es bidimensional. Tenemos

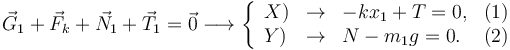
$\vec{G}_1 + \vec{F}_k + \vec{N}_1 + \vec{T}_1 = \vec{0} \longrightarrow \left\{ \begin{array}{lcll} X) & \to & -kx_1 + T = 0, & (1)\\ Y) & \to & N-m_1g = 0. & (2) \end{array} \right.$

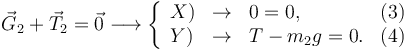
$\vec{G}_2 + \vec{T}_2 = \vec{0} \longrightarrow \left\{ \begin{array}{lcll} X) & \to & 0 = 0, & (3)\\ Y) & \to & T-m_2g = 0. & (4) \end{array} \right.$