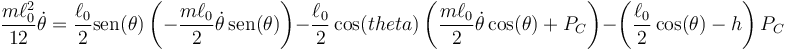Percusión sobre una barra con resorte

De Laplace

Revisión a fecha de 11:39 14 oct 2020; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Posición de equilibrio
3 Efecto de la percusión
4 Impacto con la pared
5 Tratamiento mediante dinámica analítica

1 Enunciado

Se tiene un sistema formado por una varilla de masa 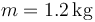$m=1.2\,\mathrm{kg}$ y longitud 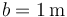$b=1\,\mathrm{m}$ , apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared está conectado a la esquina mediante un resorte de constante 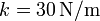$k=30\,\mathrm{N}/\mathrm{m}$ y longitud natural 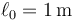$\ell_0=1\,\mathrm{m}$ . Por efecto de la gravedad (tómese 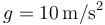$g=10\,\mathrm{m}/\mathrm{s}^2$ ) la varilla resbala hasta que la compresión del resorte la detiene.

Determine la posición de los extremos A y B de la barra en la posición de equilibrio.
Suponiendo que se encuentra en la posición de equilibrio, se efectúa sobre la barra una percusión horizontal en un punto C a una altura 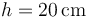$h=20\,\mathrm{cm}$ y de magnitud 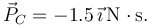$\vec{P}_C=-1.5\,\vec{\imath}\,\mathrm{N}\cdot\mathrm{s}.$ Calcule la velocidad del centro de masas inmediatamente después de la percusión, así como las percusiones de reacción en la pared y el suelo.
Tras la percusión anterior, la varilla se acerca a la pared. Calcule la velocidad del centro de masas de la varilla en el momento en que impacta con la pared.

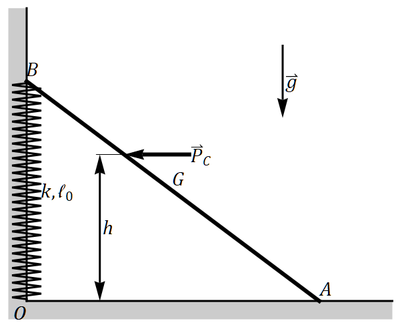
2 Posición de equilibrio

La condición de equilibrio de un sólido la da el que la resultante de las fuerzas se anule y también lo haga el momento resyltante respecto a cualquier punto.

$\vec{F}=\vec{0}\qquad\qquad \vec{M}_O=\vec{0}$

Las fuerzas que actúan sobre el sólido son

El peso

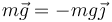
$m\vec{g}=-mg\vec{\jmath}$

La fuerza elástica debida al resorte

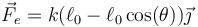
$\vec{F}_e=k(\ell_0-\ell_0\cos(\theta))\vec{\jmath}$

siendo θ el ángulo que la barra forma con la vertical

La fuerza de reacción con el suelo

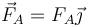
$\vec{F}_A=F_A\vec{\jmath}$

La fuerza de reacción con el suelo

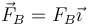
$\vec{F}_B=F_B\vec{\imath}$

La condición de resultante nula nos da las ecuaciones, separando por componentes

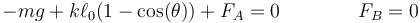
$-mg+k\ell_0(1-\cos(\theta))+F_A=0\qquad\qquad F_B=0$

Para completar el sistema necesitamos que también se anulen los momentos. Nos vale cualquier punto. Si lo hacemos respecto a la esquina, O,

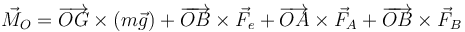
$\vec{M}_O=\overrightarrow{OG}\times(m\vec{g})+\overrightarrow{OB}\times\vec{F}_e+\overrightarrow{OA}\times\vec{F}_A+\overrightarrow{OB}\times\vec{F}_B$

Esto nos da la ecuación

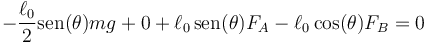
$-\frac{\ell_0}{2}\mathrm{sen}(\theta)mg+0+\ell_0\,\mathrm{sen}(\theta)F_A-\ell_0\cos(\theta)F_B=0$

de la cual obtenemos

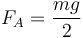
$F_A=\frac{mg}{2}$

y, por tanto,

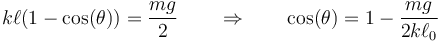
$k\ell(1-\cos(\theta))=\frac{mg}{2}\qquad\Rightarrow \qquad \cos(\theta)=1-\frac{mg}{2k\ell_0}$

siendo el valor numérico

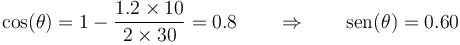
$\cos(\theta)=1-\frac{1.2\times 10}{2\times30}=0.8\qquad\Rightarrow\qquad \mathrm{sen}(\theta)=0.60$

Por ello, las posiciones de los puntos A y B se encuentran en

$\overrightarrow{OA}=\ell_0\mathrm{sen}(\theta)\vec{\imath}=0.60\vec{\imath}\,\mathrm{m}\qquad\qquad \overrightarrow{OB}=\ell_0\cos(\theta)\vec{\jmath}=0.80\vec{\jmath}\,\mathrm{m}$

3 Efecto de la percusión

Cuando se produce la percusión en C, aparecen dos percusiones de reacción en los puntos de apoyo, A y B, de forma que el sistema está sometido a tres percusiones, dos de ellas de valor desconocido

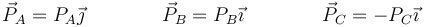
$\vec{P}_A=P_A\vec{\jmath}\qquad\qquad\vec{P}_B=P_B\vec{\imath}\qquad\qquad \vec{P}_C=-P_C\vec{\imath}$

El teorema de la cantidad de movimiento para las fuerzas impulsivas nos dice que

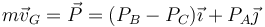
$m\vec{v}_G=\vec{P}=(P_B-P_C)\vec{\imath}+P_A\vec{\jmath}$

La velocidad del CM tras la percusión no es puramente horizontal, ya que la barra está obligada a permanecer sobre el suelo y la pared. Por ello G debe permanecer a una distancia 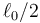$\ell_0/2$ del origen de coordenadas y su movimiento es circular

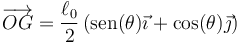
$\overrightarrow{OG}=\frac{\ell_0}{2}\left(\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath}\right)$

Derivando aquí

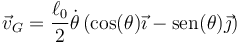
$\vec{v}_G=\frac{\ell_0}{2}\dot{\theta}\left(\cos(\theta)\vec{\imath}-\mathrm{sen}(\theta)\vec{\jmath}\right)$

Igualamos componente a componente en el TCM

$\frac{m\ell_0}{2}\dot{\theta}\cos(\theta)=P_B-P_C\qquad\qquad -\frac{m\ell_0}{2}\dot{\theta}\,\mathrm{sen}(\theta)=P_A$

Estas dos ecuaciones no son suficientes ya que tenemos tres incógnitas. La tercera ecuación sale del teorema del momento cinético

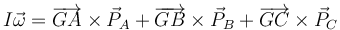
$I\vec{\omega}=\overrightarrow{GA}\times\vec{P}_A+\overrightarrow{GB}\times\vec{P}_B+\overrightarrow{GC}\times\vec{P}_C$

Respecto al CM la barra realiza un giro con velocidad angular 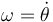$\omega =\dot{\theta}$ , siendo su momento de inercia respecto a un eje por el CM 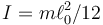$I=m\ell_0^2/12$ . Por tanto

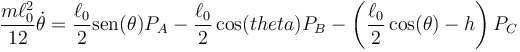
$\frac{m\ell_0^2}{12}\dot{\theta}=\frac{\ell_0}{2}\mathrm{sen}(\theta)P_A-\frac{\ell_0}{2}\cos(theta)P_B-\left(\frac{\ell_0}{2}\cos(\theta)-h\right)P_C$

Despejamos del TMC y sustituimos aquí

$\frac{m\ell_0^2}{12}\dot{\theta}=\frac{\ell_0}{2}\mathrm{sen}(\theta)\left(-\frac{m\ell_0}{2}\dot{\theta}\,\mathrm{sen}(\theta)\right)-\frac{\ell_0}{2}\cos(theta)\left(\frac{m\ell_0}{2}\dot{\theta}\cos(\theta)+P_C\right)-\left(\frac{\ell_0}{2}\cos(\theta)-h\right)P_C$

Percusión sobre una barra con resorte

De Laplace

Contenido

1 Enunciado

2 Posición de equilibrio

3 Efecto de la percusión

4 Impacto con la pared

5 Tratamiento mediante dinámica analítica

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES