Percusión sobre una barra con resorte

De Laplace

Revisión a fecha de 22:41 13 oct 2020; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Posición de equilibrio
3 Efecto de la percusión
4 Impacto con la pared
5 Tratamiento mediante dinámica analítica

1 Enunciado

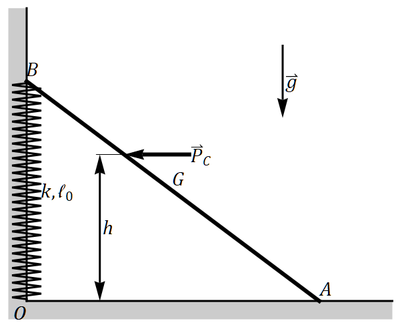
Se tiene un sistema formado por una varilla de masa 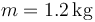$m=1.2\,\mathrm{kg}$ y longitud 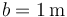$b=1\,\mathrm{m}$ , apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared está conectado a la esquina mediante un resorte de constante 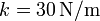$k=30\,\mathrm{N}/\mathrm{m}$ y longitud natural 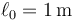$\ell_0=1\,\mathrm{m}$ . Por efecto de la gravedad (tómese 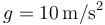$g=10\,\mathrm{m}/\mathrm{s}^2$ ) la varilla resbala hasta que la compresión del resorte la detiene.

Determine la posición de los extremos A y B de la barra en la posición de equilibrio.
Suponiendo que se encuentra en la posición de equilibrio, se efectúa sobre la barra una percusión horizontal en un punto C a una altura 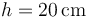$h=20\,\mathrm{cm}$ y de magnitud 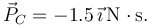$\vec{P}_C=-1.5\,\vec{\imath}\,\mathrm{N}\cdot\mathrm{s}.$ Calcule la velocidad del centro de masas inmediatamente después de la percusión, así como las percusiones de reacción en la pared y el suelo.
Tras la percusión anterior, la varilla se acerca a la pared. Calcule la velocidad del centro de masas de la varilla en el momento en que impacta con la pared.