Tres placas conductoras paralelas
De Laplace
Contenido |
1 Enunciado
Se colocan paralelamente tres placas metálicas cuadradas de 20 cm de lado y espesor despreciable, estando la primera separada de la segunda una distancia de 0.2 mm y ésta de la tercera 0.8 mm. Halle:
- La carga almacenada en cada placa.
- El potencial al que se encuentra cada una.
- El campo eléctrico entre las placas.
- La energía almacenada en el sistema.
para los siguientes casos:
- La placa central está aislada y descargada, la primera a 24 V y la tercera a tierra.
- La placa central está a 24 V y las otras dos a tierra.
- La primera está a −24 V, la central a +24 V y la tercera a tierra.
- La placa central almacena una carga de 4 nC y las dos placas exteriores están conectadas entre sí.
2 Solución general
Los tres casos pueden resolverse de una manera general por medio de la construcción de un circuito equivalente. En algunos casos puede hacerse una simplificación adicional mediante asociaciones en serie o paralelo de condensadores.
Tenemos tres conductores, que identificaremos como “1”, “2” y “3”. En un circuito equivalente, a cada conductor le corresponde un nodo, que etiquetaremos de la misma forma.
Las tres placas cuadradas forman dos condensadores planos; uno que denotaremos “a” entre la placa 1 y la 2 y otro "b" entre la 2 y la 3. Las capacidades respectivas valen
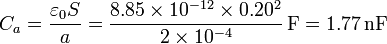
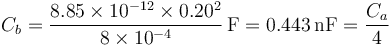
Estos condensadores están situados entre los tres nodos (uno por cada placa), de los cuales podemos conocer su carga o su potencial.

En un condensador plano, la carga en una cara de una placa es proporcional a la diferencia de potencial entre esa placa y la de la placa enfrentada
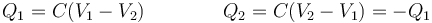
Para la placa central, que forma parte de dos condensadores, su carga total será la suma de la que tiene en sus dos caras.
Esto nos da el siguiente sistema de ecuaciones para las cargas y los potenciales
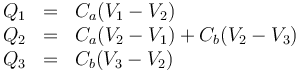
Nótese el orden en que aparecen los potenciales en los paréntesis.
Esto es un sistema de tres ecuaciones con seis incógnitas (las tres cargas y los tres potenciales). Para completarlo habrá que añadir tres ecuaciones más, que pueden ser tres datos (por ejemplo, los tres voltajes, o dos potenciales y una carga) o combinaciones de ellos (por ejemplo, que dos plcas están al mismo potencial)
Una vez que se conocen los potenciales, el campo eléctrico que va de la placa 1 a la 2 de un condensador plano vacío es
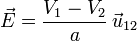
La energía de un conjunto de conductores se puede calcular como
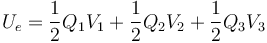
Esta misma energía puede calcularse, aplicando que la energía almacenada en cada condensador plano es proporcional al cuadrado de la diferencia de potencial
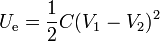
siendo la energía total del sistema
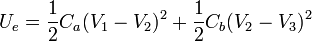
3 Primer caso
En el primer caso nos dice que la placa central está aislada y descargada
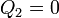
la placa 1 está a potencial fijado
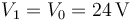
y la 3 está a tierra
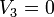
Con esto ya tenemos completo el sistema. Sustituyendo estos datos en las relaciones entre cargas y potenciales nos queda
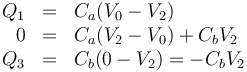
De aquí hallamos V2 despejando en la segunda
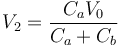
que para nuestro caso concreto es
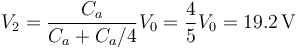
Una vez que tenemos el potencial de la placa central hallamos las cargas de las placas exteriores
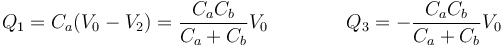
con los valores numéricos

El campo eléctrico en cada región lo hallamos a partir de cada diferencia de potencial. Si tomamos como eje Z el perpendicular a las placas y en el sentido de la 1 a la 3, queda en el primer condensador
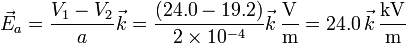
y en el segundo
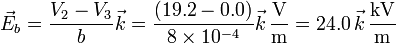
No es casual que el resultado sea el mismo. Dado que la placa central está descargada, la densidad de carga en una cara es igual a la de la otra, cambiada de signo, y por tanto el campo a los dos lados de la placa (que es igual a 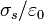 ) debe tener el mismo valor.
) debe tener el mismo valor.
La energía del sistema la podemos calcular a partir de las cargas y potenciales de los tres conductores

o por la suma de la de los condensadores
La energía almacenada la podemos hallar sumando las de los dos condensadores
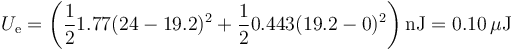
3.1 Asociación en serie
En el primer caso, la placa central está aislada y descargada (Q2 = 0). Esto implica que la carga en una de sus caras es igual y de signo opuesto a la de la otra cara, por lo que la carga de los dos condenadores es la misma.

Esto equivale a una asociación en serie de dos condensadores, cumpliendo la capacidad equivalente
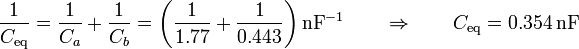
Nótese que la capacidad equivalente de una asociación en serie es menor que las dos individuales.
La diferencia de potencial en este condensador equivalente es la existente entre la primera placa y la tercera
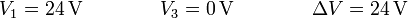
lo cual nos da las cargas en las tres placas

El voltaje de la placa central lo obtenemos de uno de los condensadores, a partir de la carga que acabamos de calcular
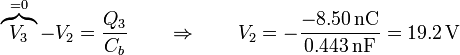
El uso del condensador equivalente nos permite hallar la energía de manera directa
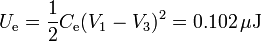
4 Segundo caso
En el segundo caso, se nos dice que los voltajes de cada una de las placas valen
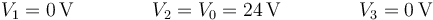
Llevando esto al sistema de ecuaciones, el cálculo de las cargas es inmediato
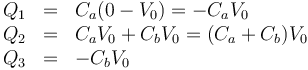
con valores numéricos
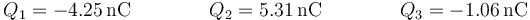
El campo entre las placas es ahora diferente en cada condensador
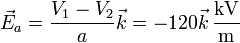
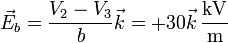
La energía acumulada se puede hallar a partir de las cargas y potenciales
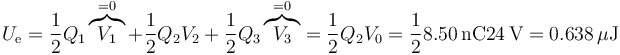
sumando la de cada condensador o a partir de la capacidad equivalente
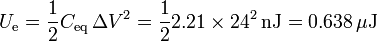
4.1 Asociación en paralelo
Alternativamente, los dos condensadores tienen uno de sus nodos al mismo potencial, el de la placa central y el otro a tierra.
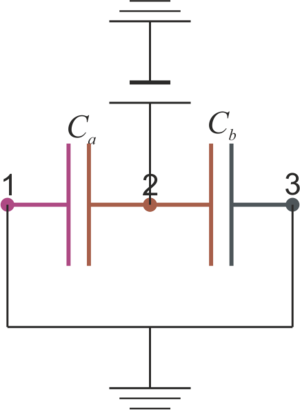
Por tanto los dos condensadores se encuentran en paralelo, siendo equivalentes a un solo condensador de capacidad
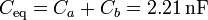
La carga de cada placa la da la diferencia de potencial en cada condensador: para la placa 1
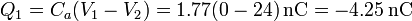
Para la 3
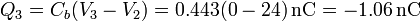
y para la placa central
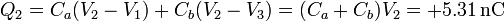
5 Tercer caso
En el último caso, la placa central no está aislada y descargada. Tampoco la diferencia de potencial es la misma en los dos condensadores. Por tanto, éstos no están ni en serie ni en paralelo, por lo que deben ser tratados separadamente.
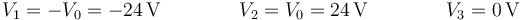
Llevando esto al sistema de ecuaciones, el cálculo de las cargas es inmediato
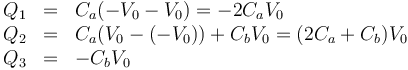
con los valores
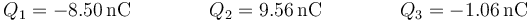
El campo entre las placas es ahora
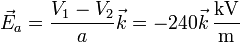
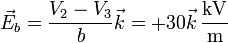
y la energía almacenada
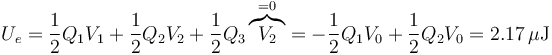
Empleando los condensadores,
tenemos que los voltajes en cada placa valen
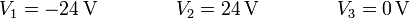
Las carga en cada una de las placas valen ahora
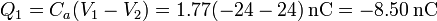
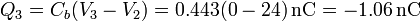
y en la placa central
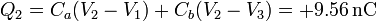
siendo al energía calculada a partir de los condensadores
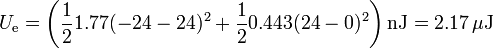
6 Cuarto caso
Por último, nos dan la carga de la placa central

y nos dicen que las dos placas exteriores están conectadas entre sí
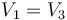
Dado que solo nos dan dos ecuaciones adicionales, nos queda un sistema de 5 ecuaciones con 6 incógnitas. Por tanto, no vamos a poder determinar todas las variables.
No obstante, veremos que se puede resolver la mayor parte del problema. Sustituyendo en las ecuaciones que ligan las cargas y los potenciales queda
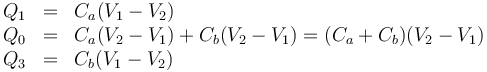
Vemos que no se puede determinar el potencial de cada placa, pero sí las diferencias de potencial entre ellas
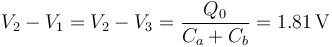
y esto nos da las cargas en las placas exteriores
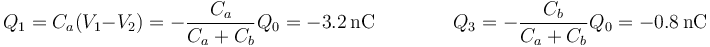
los campos eléctricos en las dos regiones
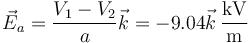

y la energía almacenada

En realidad, este sistema es similar al del segundo apartado, ya que los dos condensadores están en paralelo. La diferencia es que aquí lo que nos dan es la carga del condensador equivalente. De esta podemos hallar la d.d.p. pero no el potencial en sí. No obstante, para el cálculo del campo eléctrico (y de la energía, que se deduce de éste) basta con la diferencia de potencial, ya que el origen de potencial no influye.





